B样条插值/拟合的输入通常一组已知的数据点,曲线参数化第一步是找到一组参数,能够将这些点"固定"在某些特定值上。
例如,如果数据点是D 0 , … , D n \mathbf{D}_0, \ldots, \mathbf{D}_n D 0 , … , D n n + 1 n+1 n + 1 t 0 , … , t n t_0, \ldots, t_n t 0 , … , t n D k \mathbf{D}_k D k t k t_k t k 0 ≤ k ≤ n 0 \leq k \leq n 0 ≤ k ≤ n C ( u ) \mathbf{C}(u) C ( u ) 0 ≤ k ≤ n 0 \leq k \leq n 0 ≤ k ≤ n D k = C ( t k ) \mathbf{D}_k = \mathbf{C}(t_k) D k = C ( t k )
在下面的图中,我们有7个数据点( n = 6 ) (n=6) ( n = 6 )
参数的选择有无限多可能,我们可以均匀地划分定义域,或者从定义域中随机选择n + 1 n+1 n + 1
下图显示了4个数据点和三条插值曲线,每条曲线都使用了不同的参数。其中一条曲线向外侧弯曲,产生了凸起。黑色曲线有一个小的凸起,只有这两者之间的曲线比较符合数据点的分布趋势。因此,参数的选择会影响曲线的形状,从而相应地影响曲线的参数化。
下面,我们将讨论一些参数选择的方法,包括均匀分布法 、弦长法 和向心法 。在确定好一组参数之后,就可以计算相应的节点向量。
曲线插值、曲线逼近和曲线拟合都是用于构造一条平滑曲线来描述一组离散数据点的方法,但它们的目的和原理有所不同。
曲线插值(Curve Interpolation)
目的是找到一条平滑曲线精确地通过所有给定的数据点。
常用的插值方法包括拉格朗日插值、牛顿插值、三次样条插值等。
例如,给定一组坐标点( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) (x_1,y_1), (x_2,y_2), ..., (x_n,y_n) ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n )
曲线逼近(Curve Approximation)
目的是在某种意义下(如最小二乘法)找到最佳拟合曲线,使曲线和数据点之间的偏差最小。
常用的逼近方法包括最小二乘法拟合多项式、指数函数、三角函数等。
例如,给定一组测量数据点,我们可以用最小二乘法拟合一条直线或抛物线等简单函数来近似描述这些数据。
曲线拟合(Curve Fitting)
目的是寻找一个适当的函数形式来很好地拟合给定的数据点,使得总误差(根据不同问题有不同的误差距离的衡量方式,一般是均方误差)最小的那个简单函数。
常用的函数形式包括多项式、高斯函数、指数函数、对数函数等参数化模型。
例如,给定一组有规律的数据点,我们可以尝试用一个高斯函数或对数函数等非线性模型来很好地拟合这些数据。
插值和逼近更注重于构造一条平滑曲线来精确地通过或逼近给定的离散数据点,而拟合则更强调寻找一个合适的参数化模型函数来描述潜在的数据生成规律 ,从广义上来讲,曲线拟合包含曲线插值和曲线逼近两种情况 ,当需要拟合曲线精确经过所有给定数据点时,可以采用曲线插值的方法;当允许拟合曲线与数据点之间存在一定偏差时,可以采用曲线逼近的方法;还可以采用其他参数化模型函数(如高斯函数、对数函数等)进行非线性曲线拟合,来描述数据的内在规律。
线性回归是曲线拟合的一种特殊情况,其拟合函数形式是一条直线(一次函数) 。在线性回归中,我们试图找到一条最佳拟合直线,使得数据点到直线的残差平方和最小,这个过程就是对线性函数进行曲线拟合。
当使用线性回归模型时, 我们实际上是在用一条直线来逼近数据分布,这种用最小二乘法找到最佳拟合直线的过程,本质上属于曲线逼近的一种方法。由于线性回归模型并不要求拟合直线精确通过所有数据点,因此不属于曲线插值的范畴,但是,如果数据点刚好在一条直线上,那么线性回归得到的结果就是一个插值问题的解。
最简单的参数选择方法是均匀参数化 。假设定义域为[ 0 , 1 ] [0,1] [ 0 , 1 ] n + 1 n+1 n + 1 t 0 = 0 t_0 = 0 t 0 = 0 t n = 1 t_n = 1 t n = 1
n + 1 n+1 n + 1 [ 0 , 1 ] [0,1] [ 0 , 1 ] n n n 1 / n 1/n 1 / n 0 0 0 1 / n 1/n 1 / n 2 / n 2/n 2 / n 3 / n 3/n 3 / n ( n − 1 ) / n (n-1)/n ( n − 1 ) / n 1 1 1
t i = i n i = 0 , 1 , … , n t_i = \frac{i}{n} \quad i = 0, 1, \ldots, n
t i = n i i = 0 , 1 , … , n
例如,如果我们需要5个参数,n = 4 n = 4 n = 4 1 / 4 1/4 1 / 4 1 / 2 1/2 1 / 2 3 / 4 3/4 3 / 4 n = 7 n = 7 n = 7 1 / 7 1/7 1 / 7 2 / 7 2/7 2 / 7 3 / 7 3/7 3 / 7 4 / 7 4/7 4 / 7 5 / 7 5/7 5 / 7 6 / 7 6/7 6 / 7
如果定义域是[ a , b ] [a, b] [ a , b ] [ 0 , 1 ] [0,1] [ 0 , 1 ] [ a , b ] [a, b] [ a , b ] n + 1 n+1 n + 1 a a a b b b n n n b − a b - a b − a ( b − a ) / n (b - a)/n ( b − a ) / n
t i = a + b − a n ⋅ i i = 0 , 1 , … , n t_i = a + \frac{b - a}{n} \cdot i \quad i = 0, 1, \ldots, n
t i = a + n b − a ⋅ i i = 0 , 1 , … , n
尽管均匀参数化很简单,但它会产生一些不稳定的结果。
例如,当数据点不是均匀分布时,使用均匀分布的参数可能会产生异常形状,如凸起、尖锐点和自相交形成的环。
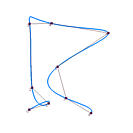
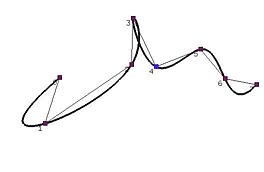
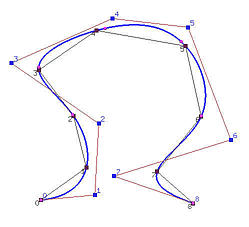
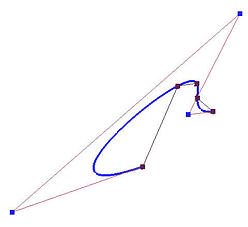
在下面的左图中,在数据点3处有一个环。在右图中,曲线在数据点1、2和3之间出现剧烈摆动。虽然不能说这些问题是均匀参数化引起的,但它确实比使用其他方法时更容易出现问题。
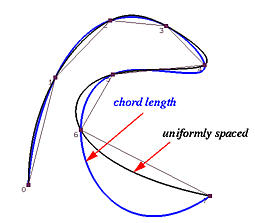
如果插值曲线和数据点连成的多边形非常接近,那么两个相邻数据点之间的曲线段长度将非常接近这两个数据点相连的弦长,并且插值曲线的总长度也非常接近数据点连成的多边形的总长度。
在下图中,插值曲线的每一段长度都非常接近其对应的弦的长度,曲线的总长度接近数据点连成的多边形的总长度。因此,如果根据弦长对定义域进行划分,划分后的节点参数与弧长参数化 产生的值近似,这就是弦长参数化 的优点。
假设数据点是 D 0 , D 1 , … , D n \mathbf{D}_0, \mathbf{D}_1, \ldots, \mathbf{D}_n D 0 , D 1 , … , D n D i − 1 \mathbf{D}_{i-1} D i − 1 D i \mathbf{D}_i D i ∣ D i − D i − 1 ∣ |\mathbf{D}_i - \mathbf{D}_{i-1}| ∣ D i − D i − 1 ∣
L = ∑ i = 1 n ∣ D i − D i − 1 ∣ L = \sum_{i=1}^{n} |\mathbf{D}_i - \mathbf{D}_{i-1}|
L = i = 1 ∑ n ∣ D i − D i − 1 ∣
因此,从点 D 0 \mathbf{D}_0 D 0 D k \mathbf{D}_k D k L k L_k L k L L L
L k = ∑ i = 1 k ∣ D i − D i − 1 ∣ L L_k=\frac{ \sum_{i=1}^{k} |\mathbf{D}_i - \mathbf{D}_{i-1}|}{L}
L k = L ∑ i = 1 k ∣ D i − D i − 1 ∣
如果我们要对插值曲线进行弦长参数化,那么定义域必须根据比率 L k L_k L k [ 0 , 1 ] [0,1] [ 0 , 1 ] t k t_k t k
t 0 = 0 t k = 1 L ( ∑ i = 1 k ∣ D i − D i − 1 ∣ ) t n = 1 \begin{aligned}
&t_{0}=0\\
&t_{k}=\frac{1}{L}\left(\sum_{i=1}^{k}|\mathbf{D}_{i}-\mathbf{D}_{i-1}|\right)\\
&t_{n}=1
\end{aligned}
t 0 = 0 t k = L 1 ( i = 1 ∑ k ∣ D i − D i − 1 ∣ ) t n = 1
其中 L L L
看一个例子:假设我们有4个数据点 ( n = 3 ) (n = 3) ( n = 3 ) D 0 = ( 0 , 0 ) \mathbf{D}_0 = (0,0) D 0 = ( 0 , 0 ) D 1 = ( 1 , 2 ) \mathbf{D}_1 = (1,2) D 1 = ( 1 , 2 ) D 2 = ( 3 , 4 ) \mathbf{D}_2 = (3,4) D 2 = ( 3 , 4 ) D 3 = ( 4 , 0 ) \mathbf{D}_3 = (4,0) D 3 = ( 4 , 0 )
∣ D 1 − D 0 ∣ = 5 = 2.236 ∣ D 2 − D 1 ∣ = 8 = 2.828 ∣ D 3 − D 2 ∣ = 17 = 4.123 |\mathbf{D}_1 - \mathbf{D}_0| = \sqrt{5} = 2.236\\
|\mathbf{D}_2 - \mathbf{D}_1| = \sqrt{8} = 2.828\\
|\mathbf{D}_3 - \mathbf{D}_2| = \sqrt{17} = 4.123
∣ D 1 − D 0 ∣ = 5 = 2 . 2 3 6 ∣ D 2 − D 1 ∣ = 8 = 2 . 8 2 8 ∣ D 3 − D 2 ∣ = 1 7 = 4 . 1 2 3
总长度是:
L = 2.236 + 2.828 + 4.123 = 9.187 L = 2.236 + 2.828 + 4.123 = 9.187
L = 2 . 2 3 6 + 2 . 8 2 8 + 4 . 1 2 3 = 9 . 1 8 7
最后,我们得到相应的参数:
t 0 = 0 t 1 = ∣ D 1 − D 0 ∣ L = 0.2434 t 2 = ∣ D 1 − D 0 ∣ + ∣ D 2 − D 1 ∣ L = 0.5512 t 3 = 1 \begin{array}{rcl}
t_0&=&0\\
t_1&=&\frac{|\mathbf{D}_1-\mathbf{D}_0|}{L}=0.2434\\
t_2&=&\frac{|\mathbf{D}_1-\mathbf{D}_0|+|\mathbf{D}_2-\mathbf{D}_1|}{L}=0.5512\\
t_3&=&1
\end{array}
t 0 t 1 t 2 t 3 = = = = 0 L ∣ D 1 − D 0 ∣ = 0 . 2 4 3 4 L ∣ D 1 − D 0 ∣ + ∣ D 2 − D 1 ∣ = 0 . 5 5 1 2 1
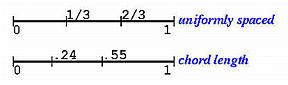
下图显示了使用均匀参数化 和弦长参数化 得到的参数分布
如果定义域是 [ a , b ] [a, b] [ a , b ] [ 0 , 1 ] [0,1] [ 0 , 1 ] L k L_k L k [ a , b ] [a, b] [ a , b ] b − a b - a b − a L k ( b − a ) L_k(b - a) L k ( b − a ) 0 ≤ k ≤ n 0 \leq k \leq n 0 ≤ k ≤ n [ 0 , b − a ] [0, b - a] [ 0 , b − a ] [ a , b ] [a, b] [ a , b ]
t 0 = a t k = a + L k ( b − a ) t n = b \begin{aligned}
&t_{0}=a\\
&t_{k}=a+L_{k}(b-a)\\
&t_{n}=b
\end{aligned}
t 0 = a t k = a + L k ( b − a ) t n = b
对多项式曲线使用弦长参数化效果并不完美,弦长只是一个近似值 。有时,较长的弦可能会导致其曲线段出现较大隆起。在下图中,黑色和蓝色曲线都使用7个数据点进行插值计算。
两条曲线的形状非常相似,除了最后一段,使用弦长参数化插值的曲线具有较大的摆动,最后几段曲线段截然不同,使用弦长法插值的蓝色曲线与使用均匀法插值的红色曲线相比,有很大的凸起和扭曲。这是弦长法经常出现的问题。
向心参数化 由E. T. Y. Lee 提出,假设我们驾驶一辆汽车穿过一个弯道绕行的赛道。在急转弯处,我们必须非常小心,以免产生过大的法向加速度(即离心力),否则我们的车辆可能会失控。为了安全驾驶,E. T. Y. Lee 建议沿路径的法向力应与角度变化成正比。向心参数化方法实际上是对这一模型的近似。我们可以将向心参数化当作是对弦长参数化方法的一种扩展。
假设数据点为 D 0 , D 1 , … , D n \mathbf{D}_0, \mathbf{D}_1, \ldots, \mathbf{D}_n D 0 , D 1 , … , D n a a a a = 1 / 2 a = 1/2 a = 1 / 2 ∣ D k − D k − 1 ∣ a |\mathbf{D}_k - \mathbf{D}_{k-1}|^a ∣ D k − D k − 1 ∣ a ∣ D k − D k − 1 ∣ |\mathbf{D}_k - \mathbf{D}_{k-1}| ∣ D k − D k − 1 ∣
因此,数据点连接成的多边形的总长度是:
L = ∑ i = 1 n ∣ D i − D i − 1 ∣ a L = \sum_{i=1}^{n} |\mathbf{D}_i - \mathbf{D}_{i-1}|^a
L = i = 1 ∑ n ∣ D i − D i − 1 ∣ a
多边形上从 D 0 \mathbf{D}_0 D 0 D k \mathbf{D}_k D k
L k = ∑ i = 1 k ∣ D i − D i − 1 ∣ a L L_k=\frac{\sum_{i=1}^k|\mathbf{D}_i-\mathbf{D}_{i-1}|^a}{L}
L k = L ∑ i = 1 k ∣ D i − D i − 1 ∣ a
因此,使用新的弦长计算方法,得到的累计弦长比例为 L 0 = 0 , L 1 , … , L n = 1 L_0 = 0, L_1, \ldots, L_n = 1 L 0 = 0 , L 1 , … , L n = 1 [ 0 , 1 ] [0,1] [ 0 , 1 ]
t 0 = 0 t k = 1 L ( ∑ i = 1 k ∣ D i − D i − 1 ∣ a ) t n = 1 \begin{array}{rcl}
t_0&=&0\\
t_k&=&\frac{1}{L}\left(\sum_{i=1}^k|\mathrm D_i-\mathrm D_{i-1}|^a\right)\\
t_n&=&1
\end{array}
t 0 t k t n = = = 0 L 1 ( ∑ i = 1 k ∣ D i − D i − 1 ∣ a ) 1
如果 a = 1 a = 1 a = 1 。如果 a < 1 a < 1 a < 1 a = 1 / 2 a = 1/2 a = 1 / 2 ∣ D k − D k − 1 ∣ a |\mathbf{D}_k - \mathbf{D}_{k-1}|^a ∣ D k − D k − 1 ∣ a ∣ D k − D k − 1 ∣ |\mathbf{D}_k - \mathbf{D}_{k-1}| ∣ D k − D k − 1 ∣ 因此,向心参数化比弦长法能够更好地处理具有较大曲率的曲线段。
下面重新计算弦长参数化中的例子,我们有四个数据点 ( n = 3 ) (n = 3) ( n = 3 ) D 0 = ( 0 , 0 ) \mathbf{D}_0 = (0,0) D 0 = ( 0 , 0 ) D 1 = ( 1 , 2 ) \mathbf{D}_1 = (1,2) D 1 = ( 1 , 2 ) D 2 = ( 3 , 4 ) \mathbf{D}_2 = (3,4) D 2 = ( 3 , 4 ) D 3 = ( 4 , 0 ) \mathbf{D}_3 = (4,0) D 3 = ( 4 , 0 ) a = 1 / 2 a = 1/2 a = 1 / 2
∣ D 1 − D 0 ∣ 1 / 2 = 5 = 1.495 ∣ D 2 − D 1 ∣ 1 / 2 = 2 2 = 1.682 ∣ D 3 − D 2 ∣ 1 / 2 = 17 = 2.031 |\mathbf{D}_1-\mathbf{D}_0|^{1/2}=\sqrt{\sqrt{5}}=1.495\\|\mathbf{D}_2-\mathbf{D}_1|^{1/2}=\sqrt{2\sqrt{2}}=1.682\\|\mathbf{D}_3-\mathbf{D}_2|^{1/2}=\sqrt{\sqrt{17}}=2.031
∣ D 1 − D 0 ∣ 1 / 2 = 5 = 1 . 4 9 5 ∣ D 2 − D 1 ∣ 1 / 2 = 2 2 = 1 . 6 8 2 ∣ D 3 − D 2 ∣ 1 / 2 = 1 7 = 2 . 0 3 1
弦的总长度是:
L = 5 + 2 2 + 17 = 5.208 L=\sqrt{\sqrt{5}}+\sqrt{2\sqrt{2}}+\sqrt{\sqrt{17}}=5.208
L = 5 + 2 2 + 1 7 = 5 . 2 0 8
因此,参数是:
t 0 = 0 t 1 = ∣ D 1 − D 0 ∣ 1 / 2 L = 0.2871 t 2 = ∣ D 1 − D 0 ∣ 1 / 2 + ∣ D 2 − D 1 ∣ 1 / 2 L = 0.6101 t 3 = 1 \begin{array}{rcl}
t_0&=&0\\
t_1&=&\frac{|\mathbf{D}_1-\mathbf{D}_0|^{1/2}}{L}=0.2871\\
t_2&=&\frac{|\mathbf{D}_1-\mathbf{D}_0|^{1/2}+|\mathbf{D}_2-\mathbf{D}_1|^{1/2}}{L}=0.6101\\
t_3&=&1
\end{array}
t 0 t 1 t 2 t 3 = = = = 0 L ∣ D 1 − D 0 ∣ 1 / 2 = 0 . 2 8 7 1 L ∣ D 1 − D 0 ∣ 1 / 2 + ∣ D 2 − D 1 ∣ 1 / 2 = 0 . 6 1 0 1 1
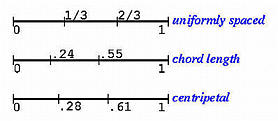
下面给出了使用均匀参数化、弦长参数化和向心参数化计算的三组参数的分布情况:
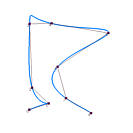
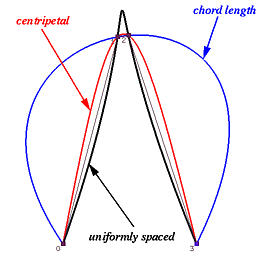
下面看一个极端的例子,下图显示了使用均匀参数化(黑色)、弦长参数化(蓝色)和向心参数化(红色)对4个数据点进行插值得到的B样条曲线。均匀参数化得到的曲线有一个峰值,弦长参数化得到的曲线有两个大的凸起,向心参数化则很好地处理了两个距离非常接近的数据点(1号点和2号点)。
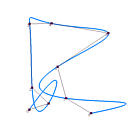
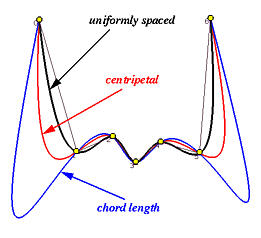
那么可以说向心参数化比其他两种方法更好吗?下面是一个反例。我们有7个数据点,黑色、蓝色和红色曲线是使用均匀参数化、弦长参数化和向心参数化插值得到的曲线。如图所示,均匀参数化产生了一个非常稳定的插值曲线,向心参数化得到的曲线波动大于均匀参数化得到的曲线,而弦长参数化产生的曲线波动幅度最大。
1999年,Choong-Gyoo Lim 提出了一种有趣的参数化方法。在之前讨论的方法中,我们先确定参数,然后计算一个节点向量。Lim提出的方法称为通用方法 ,通过使用均匀分布的节点来计算参数,正好相反。
假设我们需要n + 1 n+1 n + 1 p p p m + 1 m+1 m + 1 m = n + p + 1 m = n + p + 1 m = n + p + 1 p + 1 p+1 p + 1 p + 1 p+1 p + 1 n − p n-p n − p [ 0 , 1 ] [0,1] [ 0 , 1 ]
u 0 = u 1 = ⋯ = u p = 0 u p + i = i n − p + 1 f o r i = 1 , 2 , … , n − p u m − p = u m − p + 1 = ⋯ = u m = 1 \begin{aligned}
u_{0}&=\quad u_1=\cdots=u_p=0\\
u_{p+i}&=\quad\frac i{n-p+1}\quad\mathrm{for~}i=1,2,\ldots,n-p\\
u_{m-p}&=\quad u_{m-p+1}=\cdots=u_m=1
\end{aligned}
u 0 u p + i u m − p = u 1 = ⋯ = u p = 0 = n − p + 1 i f o r i = 1 , 2 , … , n − p = u m − p + 1 = ⋯ = u m = 1
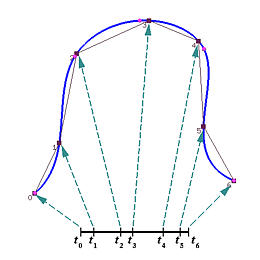
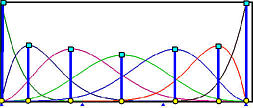
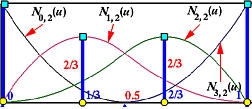
这样我们就有了 n + 1 n+1 n + 1 B样条基函数 。然后,选择对应基函数达到最大值时的参数作为数据点的参数。如下图所示,其中n = 6 n = 6 n = 6 p = 4 p = 4 p = 4 m = 11 m = 11 m = 1 1 n + 1 n+1 n + 1
看一个例子。假设我们有4个数据点(n = 3 n=3 n = 3 p = 2 p=2 p = 2 m = n + p + 1 = 6 m = n + p + 1 = 6 m = n + p + 1 = 6
u 0 = u 1 = u 2 = 0 , u 3 = 0.5 , u 4 = u 5 = u 6 = 1 u_0 = u_1 = u_2 = 0, \quad u_3 = 0.5, \quad u_4 = u_5 = u_6 = 1
u 0 = u 1 = u 2 = 0 , u 3 = 0 . 5 , u 4 = u 5 = u 6 = 1
然后,我们可以计算B样条基函数。从第0阶开始:
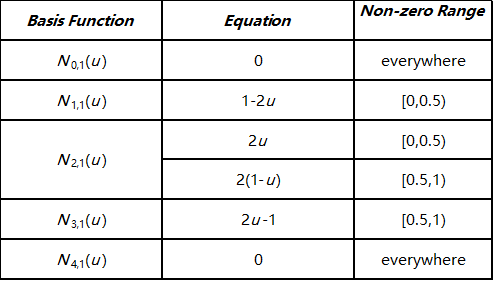
接下来,我们计算次数为1的基函数。由于N 0 , 0 ( u ) N_{0,0}(u) N 0 , 0 ( u ) N 1 , 0 ( u ) N_{1,0}(u) N 1 , 0 ( u ) N 0 , 1 ( u ) N_{0,1}(u) N 0 , 1 ( u ) N 4 , 1 ( u ) N_{4,1}(u) N 4 , 1 ( u ) N 1 , 1 ( u ) N_{1,1}(u) N 1 , 1 ( u ) N 2 , 1 ( u ) N_{2,1}(u) N 2 , 1 ( u ) N 3 , 1 ( u ) N_{3,1}(u) N 3 , 1 ( u )
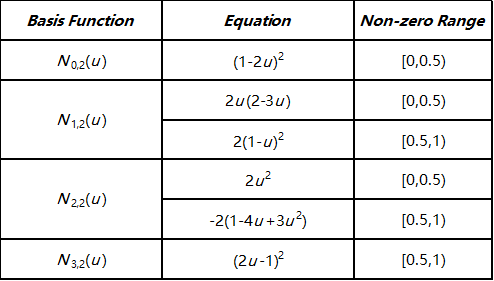
次数为2的基函数如下:
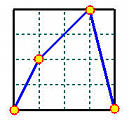
下面的图显示了所有四个次数为2的B样条基函数。
不难算出,N 0 , 2 ( u ) N_{0,2}(u) N 0 , 2 ( u ) N 1 , 2 ( u ) N_{1,2}(u) N 1 , 2 ( u ) N 2 , 2 ( u ) N_{2,2}(u) N 2 , 2 ( u ) N 3 , 2 ( u ) N_{3,2}(u) N 3 , 2 ( u ) u = 0 u = 0 u = 0 u = 1 / 3 u = 1/3 u = 1 / 3 u = 2 / 3 u = 2/3 u = 2 / 3 u = 1 u = 1 u = 1
因此,使用通用方法,得到的节点向量是0 , 0 , 0 , 0.5 , 1 , 1 , 1 {0, 0, 0, 0.5, 1, 1, 1} 0 , 0 , 0 , 0 . 5 , 1 , 1 , 1 0 , 1 / 3 , 2 / 3 , 1 {0, 1/3, 2/3, 1} 0 , 1 / 3 , 2 / 3 , 1
使用通用参数化方法插值得到的曲线有一个非常有用的性质。它是仿射不变的 。这意味着,可以通过变换数据点来获得变换后的插值B样条曲线。这与B样条曲线的仿射不变性质类似。
如果在原始插值曲线和变换后的插值B样条曲线中使用相同的节点和参数集,那么通过变换数据点来实现曲线的变换。根据这一点,我们知道均匀参数化也是仿射不变的 ,因为节点向量是从一组均匀分布的参数计算出来的,这些参数在变换前后没有改变。然而,弦长参数化和向心参数化不是仿射不变的 ,因为变换后的曲线中,弦长分布可能与原始的不一样,我们会得到一组新的弦长,必须重新计算新的参数。
由e + 1 e+1 e + 1 f + 1 f+1 f + 1 ( p , q ) (p, q) ( p , q )
S ( u , v ) = ∑ i = 0 e ∑ j = 0 f N i , p ( u ) N j , q ( v ) P i j \mathbf{S}(u,v) = \sum_{i=0}^{e} \sum_{j=0}^{f} N_{i,p}(u)N_{j,q}(v)\mathbf{P}_{ij}
S ( u , v ) = i = 0 ∑ e j = 0 ∑ f N i , p ( u ) N j , q ( v ) P i j
它需要两组参数(参数点)来进行曲面插值和逼近。
假设我们有m + 1 m+1 m + 1 n + 1 n+1 n + 1 D i j \mathbf{D}_{ij} D i j 0 ≤ i ≤ m , 0 ≤ j ≤ n 0 \leq i \leq m,0 \leq j \leq n 0 ≤ i ≤ m , 0 ≤ j ≤ n u u u m + 1 m+1 m + 1 s 0 , . . . , s m s_0, ..., s_m s 0 , . . . , s m v v v n + 1 n+1 n + 1 t 0 , . . . , t n t_0, ..., t_n t 0 , . . . , t n ( s c , t d ) (s_c, t_d) ( s c , t d ) S ( s c , t d ) \mathbf{S}(s_c, t_d) S ( s c , t d )
S ( s c , t d ) = ∑ i = 0 e ∑ j = 0 f N i , p ( s c ) N j , q ( t d ) P i j \mathbf{S}(s_c, t_d) = \sum_{i=0}^{e} \sum_{j=0}^{f} N_{i,p}(s_c)N_{j,q}(t_d)\mathbf{P}_{ij}
S ( s c , t d ) = i = 0 ∑ e j = 0 ∑ f N i , p ( s c ) N j , q ( t d ) P i j
而S ( s c , t d ) \mathbf{S}(s_c, t_d) S ( s c , t d ) D c d \mathbf{D}_{cd} D c d s c s_c s c t d t_d t d u u u v v v
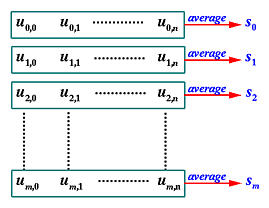
在B样条曲面方程中,u u u N i , p ( u ) N_{i,p}(u) N i , p ( u ) P i j \mathbf{P}_{ij} P i j i i i i i i m m m N 0 , p ( u ) , N 1 , p ( u ) , . . . , N m , p ( u ) N_{0,p}(u), N_{1,p}(u), ..., N_{m,p}(u) N 0 , p ( u ) , N 1 , p ( u ) , . . . , N m , p ( u ) u u u m + 1 m+1 m + 1 p p p j j j m + 1 m+1 m + 1 u 0 , j , u 1 , j , . . . , u m , j u_{0,j}, u_{1,j}, ..., u_{m,j} u 0 , j , u 1 , j , . . . , u m , j s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m s i s_i s i i i i s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 ) s_i = (u_{i,0} + u_{i,1} + ... + u_{i,n})/(n+1) s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 ) u u u N i , p ( u ) N_{i,p}(u) N i , p ( u ) P i j \mathbf{P}_{ij} P i j i i i i i i m m m N 0 , p ( u ) , N 1 , p ( u ) , . . . , N m , p ( u ) N_{0,p}(u), N_{1,p}(u), ..., N_{m,p}(u) N 0 , p ( u ) , N 1 , p ( u ) , . . . , N m , p ( u ) u u u m + 1 m+1 m + 1 p p p j j j m + 1 m+1 m + 1 u 0 , j , u 1 , j , . . . , u m , j u_{0,j}, u_{1,j}, ..., u_{m,j} u 0 , j , u 1 , j , . . . , u m , j s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m s i s_i s i i i i s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 ) s_i = (u_{i,0} + u_{i,1} + ... + u_{i,n})/(n+1) s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 )
v v v n + 1 n+1 n + 1 n + 1 n+1 n + 1 i i i n + 1 n+1 n + 1 v i , 0 , v i , 1 , . . . , v i , n v_{i,0}, v_{i,1}, ..., v_{i,n} v i , 0 , v i , 1 , . . . , v i , n m + 1 m+1 m + 1 ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) t j t_j t j j j j t j = ( v 0 , j + v 1 , j + . . . + v m , j ) / ( m + 1 ) t_j = (v_{0,j} + v_{1,j} + ... + v_{m,j})/(m+1) t j = ( v 0 , j + v 1 , j + . . . + v m , j ) / ( m + 1 ) n + 1 n+1 n + 1 v v v
算法总结如下:
Input: ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) D i j \mathbf{D}_{ij} D i j Output: u u u s 0 , . . . , s m s_0, ..., s_m s 0 , . . . , s m v v v t 0 , . . . , t n t_0, ..., t_n t 0 , . . . , t n
算法:
// 计算 s 0 , . . . , s m s_0, ..., s_m s 0 , . . . , s m for j j j 0 0 0 to n n n do m + 1 m+1 m + 1 u 0 , j , u 1 , j , . . . , u m , j u_{0,j}, u_{1,j}, ..., u_{m,j} u 0 , j , u 1 , j , . . . , u m , j for i i i 0 0 0 to m m m do s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 ) s_i = (u_{i,0} + u_{i,1} + ... + u_{i,n})/(n+1) s i = ( u i , 0 + u i , 1 + . . . + u i , n ) / ( n + 1 ) u u u
// 计算 t 0 , . . . , t n t_0, ..., t_n t 0 , . . . , t n for i i i 0 0 0 to m m m do n + 1 n+1 n + 1 v i , 0 , v i , 1 , . . . , v i , n v_{i,0}, v_{i,1}, ..., v_{i,n} v i , 0 , v i , 1 , . . . , v i , n for j j j 0 0 0 to n n n do t j = ( v 0 , j + v 1 , j + . . . + v m , j ) / ( m + 1 ) t_j = (v_{0,j} + v_{1,j} + ... + v_{m,j})/(m+1) t j = ( v 0 , j + v 1 , j + . . . + v m , j ) / ( m + 1 ) v v v
根据参数 s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m p p p u u u U U U t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n q q q v v v V V V
注意,上述只是一个概念性算法,效率不高。这个算法只适用于均匀参数化、弦长参数化和向心参数化 。对于通用参数化方法,因为不涉及数据点,我们可以对每一行和每一列的数据点应用均匀分布的节点来计算参数。
插值和逼近的计算过程中都会涉及到求解线性方程组,下面我们讨论一个常用的求解方法。
假设我们有一个 n × n n \times n n × n A \mathbf{A} A n × h n \times h n × h B \mathbf{B} B n × h n \times h n × h X \mathbf{X} X
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] n × n \mathbf{A} = \left[\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{array}\right]_{n\times n}
A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a n 1 a 1 2 a 2 2 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ n × n
B = [ b 11 b 12 ⋯ b 1 h b 21 b 22 ⋯ b 2 h ⋮ ⋮ ⋱ ⋮ b n 1 b n 2 ⋯ b n h ] n × h \mathbf{B} = \left[\begin{array}{cccc}b_{11}&b_{12}&\cdots&b_{1h}\\b_{21}&b_{22}&\cdots&b_{2h}\\\vdots&\vdots&\ddots&\vdots\\b_{n1}&b_{n2}&\cdots&b_{nh}\end{array}\right]_{n\times h}
B = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 1 b 2 1 ⋮ b n 1 b 1 2 b 2 2 ⋮ b n 2 ⋯ ⋯ ⋱ ⋯ b 1 h b 2 h ⋮ b n h ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ n × h
X = [ x 11 x 12 ⋯ x 1 h x 21 x 22 ⋯ x 2 h ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n h ] n × h \mathbf{X} = \left[\begin{array}{cccc}x_{11}&x_{12}&\cdots&x_{1h}\\x_{21}&x_{22}&\cdots&x_{2h}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{nh}\end{array}\right]_{n\times h}
X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 1 x 2 1 ⋮ x n 1 x 1 2 x 2 2 ⋮ x n 2 ⋯ ⋯ ⋱ ⋯ x 1 h x 2 h ⋮ x n h ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ n × h
它们满足以下关系:
B = A ⋅ X \mathbf{B} = \mathbf{A}\cdot\mathbf{X}
B = A ⋅ X
如果 A \mathbf{A} A B \mathbf{B} B X \mathbf{X} X A \mathbf{A} A A − 1 \mathbf{A}^{-1} A − 1 X \mathbf{X} X A − 1 B \mathbf{A}^{-1}\mathbf{B} A − 1 B
一个有效的求解 B \mathbf{B} B A X \mathbf{A}\mathbf{X} A X LU分解是一种加速计算的方法 。
LU分解首先将矩阵 A \mathbf{A} A A = L U \mathbf{A} = \mathbf{L} \mathbf{U} A = L U L \mathbf{L} L U \mathbf{U} U A \mathbf{A} A n × n n \times n n × n L \mathbf{L} L U \mathbf{U} U n × n n \times n n × n
L = [ l 11 0 0 ⋯ 0 l 21 l 22 0 ⋯ 0 ⋮ ⋮ ⋱ ⋱ ⋮ l n 1 l n 2 l n 3 ⋯ l n n ] U = [ u 11 u 12 u 13 ⋯ u 1 n 0 u 22 u 23 ⋯ u 2 n 0 0 u 33 ⋯ u 3 n ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ u n n ] \mathbf{L} = \left[\begin{array}{ccccc}l_{11}&0&0&\cdots&0\\l_{21}&l_{22}&0&\cdots&0\\\vdots&\vdots&\ddots&\ddots&\vdots\\l_{n1}&l_{n2}&l_{n3}&\cdots&l_{nn}\end{array}\right]\quad\mathbf{U} = \left[\begin{array}{ccccc}u_{11}&u_{12}&u_{13}&\cdots&u_{1n}\\0&u_{22}&u_{23}&\cdots&u_{2n}\\0&0&u_{33}&\cdots&u_{3n}\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&u_{nn}\end{array}\right]
L = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ l 1 1 l 2 1 ⋮ l n 1 0 l 2 2 ⋮ l n 2 0 0 ⋱ l n 3 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ l n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ U = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 1 0 0 ⋮ 0 u 1 2 u 2 2 0 ⋮ 0 u 1 3 u 2 3 u 3 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ u 1 n u 2 n u 3 n ⋮ u n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
下三角矩阵 L \mathbf{L} L U \mathbf{U} U
如果找到了满足 A = L U \mathbf{A} = \mathbf{L} \mathbf{U} A = L U L U \mathbf{L} \mathbf{U} L U B = ( L U ) X \mathbf{B} = (\mathbf{L} \mathbf{U}) \mathbf{X} B = ( L U ) X B = L ( U X ) \mathbf{B} = \mathbf{L} (\mathbf{U} \mathbf{X}) B = L ( U X )
由于 L \mathbf{L} L B \mathbf{B} B B = L Y \mathbf{B} = \mathbf{L} \mathbf{Y} B = L Y Y = U X \mathbf{Y} = \mathbf{U} \mathbf{X} Y = U X U \mathbf{U} U Y \mathbf{Y} Y X \mathbf{X} X
这样,求解方程B = A X \mathbf{B} = \mathbf{A}\mathbf{X} B = A X
从 B = L Y \mathbf{B} = \mathbf{L} \mathbf{Y} B = L Y Y \mathbf{Y} Y
从 Y = U X \mathbf{Y} = \mathbf{U} \mathbf{X} Y = U X X \mathbf{X} X
第一步,展开 B = L Y \mathbf{B} = \mathbf{L} \mathbf{Y} B = L Y
[ b 11 b 12 ⋯ b 1 h b 21 b 22 ⋯ b 2 h ⋮ ⋮ ⋱ ⋮ b n 1 b n 2 ⋯ b n h ] = [ l 11 0 ⋯ 0 l 21 l 22 ⋯ 0 ⋮ ⋮ ⋱ ⋮ l n 1 l n 2 ⋯ l n n ] [ y 11 y 12 ⋯ y 1 h y 21 y 22 ⋯ y 2 h ⋮ ⋮ ⋱ ⋮ y n 1 y n 2 ⋯ y n h ] \begin{bmatrix}
b_{11} & b_{12} & \cdots & b_{1h} \\
b_{21} & b_{22} & \cdots & b_{2h} \\
\vdots & \vdots & \ddots & \vdots \\
b_{n1} & b_{n2} & \cdots & b_{nh}
\end{bmatrix}
=
\begin{bmatrix}
l_{11} & 0 & \cdots & 0 \\
l_{21} & l_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
l_{n1} & l_{n2} & \cdots & l_{nn}
\end{bmatrix}
\begin{bmatrix}
y_{11} & y_{12} & \cdots & y_{1h} \\
y_{21} & y_{22} & \cdots & y_{2h} \\
\vdots & \vdots & \ddots & \vdots \\
y_{n1} & y_{n2} & \cdots & y_{nh}
\end{bmatrix}
⎣ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 1 b 2 1 ⋮ b n 1 b 1 2 b 2 2 ⋮ b n 2 ⋯ ⋯ ⋱ ⋯ b 1 h b 2 h ⋮ b n h ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ l 1 1 l 2 1 ⋮ l n 1 0 l 2 2 ⋮ l n 2 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ l n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 1 y 2 1 ⋮ y n 1 y 1 2 y 2 2 ⋮ y n 2 ⋯ ⋯ ⋱ ⋯ y 1 h y 2 h ⋮ y n h ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
不难看出矩阵 B \mathbf{B} B j j j L \mathbf{L} L Y \mathbf{Y} Y j j j Y \mathbf{Y} Y
[ b 1 b 2 ⋮ b n ] = [ l 11 0 0 ⋯ 0 l 21 l 22 0 ⋯ 0 ⋮ ⋮ ⋱ ⋱ ⋮ l n 1 l n 2 l n 3 ⋯ l n n ] ⋅ [ y 1 y 2 ⋮ y n ] \left[\begin{array}{c}b_1\\b_2\\\vdots\\b_n\end{array}\right] = \left[\begin{array}{ccccc}l_{11}&0&0&\cdots&0\\l_{21}&l_{22}&0&\cdots&0\\\vdots&\vdots&\ddots&\ddots&\vdots\\l_{n1}&l_{n2}&l_{n3}&\cdots&l_{nn}\end{array}\right]\cdot\left[\begin{array}{c}y_1\\y_2\\\vdots\\y_n\end{array}\right]
⎣ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 b 2 ⋮ b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ l 1 1 l 2 1 ⋮ l n 1 0 l 2 2 ⋮ l n 2 0 0 ⋱ l n 3 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ l n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⋅ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
上式相当于方程:
b 1 = l 11 y 1 b 2 = l 21 y 1 + l 22 y 2 ⋮ ⋮ b n = l n 1 y 1 + l n 2 y 2 + l n 3 y 3 + ⋯ + l n n y n \begin{array}{rcl}
b_1&=&l_{11}y_1\\
b_2&=&l_{21}y_1&+&l_{22}y_2\\
&\vdots&\vdots\\
b_n&=&l_{n1}y_1&+&l_{n2}y_2&+&l_{n3}y_3&+&\cdots&+&l_{nn}y_n
\end{array}
b 1 b 2 b n = = ⋮ = l 1 1 y 1 l 2 1 y 1 ⋮ l n 1 y 1 + + l 2 2 y 2 l n 2 y 2 + l n 3 y 3 + ⋯ + l n n y n
从上面的等式中,我们可以算出 y 1 = b 1 l 11 y_1 = \frac{b_1}{l_{11}} y 1 = l 1 1 b 1 y 1 y_1 y 1 y 2 = b 2 − l 21 y 1 l 22 y_2 = \frac{b_2 - l_{21}y_1}{l_{22}} y 2 = l 2 2 b 2 − l 2 1 y 1 y 1 y_1 y 1 y 2 y_2 y 2 y 3 = b 3 − ( l 31 y 1 + l 32 y 2 ) l 33 y_3 = \frac{b_3 - (l_{31}y_1 + l_{32}y_2)}{l_{33}} y 3 = l 3 3 b 3 − ( l 3 1 y 1 + l 3 2 y 2 )
因此,我们从第一个方程计算 y 1 y_1 y 1 y 2 y_2 y 2 y 1 y_1 y 1 y 2 y_2 y 2 y 3 y_3 y 3 i i i y 1 , y 2 , … , y i − 1 y_1, y_2, \ldots, y_{i-1} y 1 , y 2 , … , y i − 1 i − 1 i-1 i − 1 i i i y i y_i y i
y i = 1 l i i [ b i − ∑ k = 1 i − 1 l i , k y k ] y_i = \frac{1}{l_{ii}}\left[b_i-\sum_{k=1}^{i-1}l_{i,k}y_k\right]
y i = l i i 1 [ b i − k = 1 ∑ i − 1 l i , k y k ]
由于 y i y_i y i y i + 1 y_{i+1} y i + 1 前向代换 。重复以上过程,可以求解出向量 Y \mathbf{Y} Y
下面是算法的流程:
Input: 矩阵 B n × h \mathbf{B}_{n \times h} B n × h L n × n \mathbf{L}_{n \times n} L n × n Output: 矩阵 Y n × h \mathbf{Y}_{n \times h} Y n × h
算法:
for j j j 1 1 1 to h h h do // 共有 h h h begin // 对每一列执行以下操作y 1 , j = b 1 , j / l 1 , 1 y_{1,j} = b_{1,j} / l_{1,1} y 1 , j = b 1 , j / l 1 , 1 y 1 y_1 y 1 for i i i 2 2 2 to n n n do // 处理该列的元素begin s u m = 0 sum = 0 s u m = 0 y i y_i y i for k k k 1 1 1 to i − 1 i-1 i − 1 do s u m = s u m + l i , k × y k , j sum = sum + l_{i,k} \times y_{k,j} s u m = s u m + l i , k × y k , j y i , j = ( b i , j − s u m ) / l i , i y_{i,j} = (b_{i,j} - sum) / l_{i,i} y i , j = ( b i , j − s u m ) / l i , i end end
求解出Y \mathbf{Y} Y Y = U X \mathbf{Y} = \mathbf{U} \mathbf{X} Y = U X X \mathbf{X} X Y \mathbf{Y} Y X \mathbf{X} X
[ y 1 y 2 ⋮ y n ] = [ u 11 u 12 u 13 ⋯ u 1 n 0 u 22 u 23 ⋯ u 2 n 0 0 u 33 ⋯ u 3 n ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ u n n ] ⋅ [ x 1 x 2 ⋮ x n ] \left[\begin{array}{c}y_1\\y_2\\\vdots\\y_n\end{array}\right]=\left[\begin{array}{ccccc}u_{11}&u_{12}&u_{13}&\cdots&u_{1n}\\0&u_{22}&u_{23}&\cdots&u_{2n}\\0&0&u_{33}&\cdots&u_{3n}\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&u_{nn}\end{array}\right]\cdot\left[\begin{array}{c}x_1\\x_2\\\vdots\\x_n\end{array}\right]
⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 1 0 0 ⋮ 0 u 1 2 u 2 2 0 ⋮ 0 u 1 3 u 2 3 u 3 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ u 1 n u 2 n u 3 n ⋮ u n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⋅ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 ⋮ x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
等价于方程:
y 1 = u 11 x 1 + u 12 x 2 + u 13 x 3 + ⋯ + u 1 n x n y 2 = u 22 x 2 + u 23 x 3 + + u 2 n x n ⋮ ⋱ y n = u n n x n \begin{array}{cccccccccc}y_1&=&u_{11}x_1&+&u_{12}x_2&+&u_{13}x_3&+&\cdots&+&u_{1n}x_n\\y_2&=&&&u_{22}x_2&+&u_{23}x_3&+&&+&u_{2n}x_n\\&\vdots&&&&&\ddots&&&&\\y_n&=&&&&&&&&u_{nn}x_n\end{array}
y 1 y 2 y n = = ⋮ = u 1 1 x 1 + u 1 2 x 2 u 2 2 x 2 + + u 1 3 x 3 u 2 3 x 3 ⋱ + + ⋯ + + u n n x n u 1 n x n u 2 n x n
现在,可以从第 n n n x n x_n x n x n = y n u n n x_n = \frac{y_n}{u_{nn}} x n = u n n y n
一旦 x n x_n x n n − 1 n-1 n − 1 y n − 1 = u n − 1 , n − 1 x n − 1 + u n − 1 , n x n y_{n-1} = u_{n-1,n-1}x_{n-1} + u_{n-1,n}x_n y n − 1 = u n − 1 , n − 1 x n − 1 + u n − 1 , n x n x n − 1 x_{n-1} x n − 1
x n − 1 = y n − 1 − u n − 1 , n x n u n − 1 , n − 1 x_{n-1} = \frac{y_{n-1} - u_{n-1,n}x_n}{u_{n-1,n-1}}
x n − 1 = u n − 1 , n − 1 y n − 1 − u n − 1 , n x n
现在,我们有 x n x_n x n x n − 1 x_{n-1} x n − 1 n − 2 n-2 n − 2 y n − 2 = u n − 2 , n − 2 x n − 2 + u n − 2 , n − 1 x n − 1 + u n − 2 , n x n y_{n-2} = u_{n-2,n-2}x_{n-2} + u_{n-2,n-1}x_{n-1} + u_{n-2,n}x_n y n − 2 = u n − 2 , n − 2 x n − 2 + u n − 2 , n − 1 x n − 1 + u n − 2 , n x n x n − 2 x_{n-2} x n − 2
x n − 2 = y n − 2 − ( u n − 2 , n − 1 x n − 1 + u n − 2 , n x n ) u n − 2 , n − 2 x_{n-2} = \frac{y_{n-2} - (u_{n-2,n-1}x_{n-1} + u_{n-2,n}x_n)}{u_{n-2,n-2}}
x n − 2 = u n − 2 , n − 2 y n − 2 − ( u n − 2 , n − 1 x n − 1 + u n − 2 , n x n )
从 x n , x n − 1 x_n, x_{n-1} x n , x n − 1 x n − 2 x_{n-2} x n − 2 n − 3 n-3 n − 3 x n − 3 x_{n-3} x n − 3 x n , x n − 1 , … , x i + 1 x_n, x_{n-1}, \ldots, x_{i+1} x n , x n − 1 , … , x i + 1 i i i x i x_i x i
x i = 1 u i i [ y i − ∑ k = i + 1 n u i , k x k ] x_{i} = \frac{1}{u_{ii}}\left[y_{i}-\sum_{k=i+1}^{n}u_{i,k}x_{k}\right]
x i = u i i 1 [ y i − k = i + 1 ∑ n u i , k x k ]
重复这个过程直到计算出 x 1 x_1 x 1 x x x
以下算法总结了这个过程:
Input: 矩阵 Y n × h \mathbf{Y}_{n \times h} Y n × h U n × n \mathbf{U}_{n \times n} U n × n Output: 矩阵 X n × h \mathbf{X}_{n \times h} X n × h
算法:
for j j j 1 1 1 to h h h do // 共有 h h h begin // 对每一列执行以下操作x n , j = y n , j / u n , n x_{n,j} = y_{n,j} / u_{n,n} x n , j = y n , j / u n , n x n x_n x n for i i i n − 1 n-1 n − 1 downto 1 1 1 do // 处理该列的元素begin s u m = 0 sum = 0 s u m = 0 x i x_i x i for k k k i + 1 i+1 i + 1 to n n n do s u m = s u m + u i , k × x k , j sum = sum + u_{i,k} \times x_{k,j} s u m = s u m + u i , k × x k , j x i , j = ( y i , j − s u m ) / u i , i x_{i,j} = (y_{i,j} - sum) / u_{i,i} x i , j = ( y i , j − s u m ) / u i , i end end
这次我们首先计算 x n x_n x n x n − 1 x_{n-1} x n − 1 x 1 x_1 x 1 后向代换 。
要用一组点拟合出B样条曲线,最简单的方法是使用全局插值 方法。
假设我们有n + 1 n+1 n + 1 D 0 \mathbf{D}_0 D 0 D 1 \mathbf{D}_1 D 1 D n \mathbf{D}_n D n p p p p ≤ n p \leq n p ≤ n t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n t k t_k t k D k \mathbf{D}_k D k m + 1 m+1 m + 1 m = n + p + 1 m = n + p + 1 m = n + p + 1 p p p n + 1 n+1 n + 1 全局插值法 就是用来找到这些控制点的一种方法。
全局曲线插值 :给定一组n + 1 n+1 n + 1 D 0 , D 2 , . . . , D n D_0, D_2, ..., D_n D 0 , D 2 , . . . , D n p p p n + 1 n+1 n + 1 p p p
假设次数为p p p
C ( u ) = ∑ i = 0 n N i , p ( u ) P i C(u) = \sum_{i=0}^{n} N_{i,p}(u)P_i
C ( u ) = i = 0 ∑ n N i , p ( u ) P i
这个B样条曲线有n + 1 n+1 n + 1 t k t_k t k D k \mathbf{D}_k D k t k t_k t k
D k = C ( t k ) = ∑ i = 0 n N i , p ( t k ) P i 0 ≤ k ≤ n \mathbf{D}_k = C(t_k) = \sum_{i=0}^{n} N_{i,p}(t_k)P_i \quad 0 \leq k \leq n
D k = C ( t k ) = i = 0 ∑ n N i , p ( t k ) P i 0 ≤ k ≤ n
上述方程中有n + 1 n+1 n + 1 N 0 , p ( u ) N_{0,p}(u) N 0 , p ( u ) N 1 , p ( u ) N_{1,p}(u) N 1 , p ( u ) N 2 , p ( u ) N_{2,p}(u) N 2 , p ( u ) N n , p ( u ) N_{n,p}(u) N n , p ( u ) n + 1 n+1 n + 1 t 0 , t 1 , t 2 , . . , 和 t n t_0, t_1, t_2, .., 和 t_n t 0 , t 1 , t 2 , . . , 和 t n t k t_k t k N i , p ( u ) N_{i,p}(u) N i , p ( u ) ( n + 1 ) 2 (n +1)^2 ( n + 1 ) 2 ( n + 1 ) × ( n + 1 ) (n +1) \times (n +1) ( n + 1 ) × ( n + 1 ) N \mathbf{N} N k k k t k t_k t k N 0 , p ( u ) N_{0,p}(u) N 0 , p ( u ) N 1 , p ( u ) N_{1,p}(u) N 1 , p ( u ) N 2 , p ( u ) N_{2,p}(u) N 2 , p ( u ) N i , p ( u ) N_{i,p}(u) N i , p ( u )
N = [ N 0 , p ( t 0 ) N 1 , p ( t 0 ) ⋯ N n , p ( t 0 ) N 0 , p ( t 1 ) N 1 , p ( t 1 ) ⋯ N n , p ( t 1 ) ⋮ ⋮ ⋱ ⋮ N 0 , p ( t n ) N 1 , p ( t n ) ⋯ N n , p ( t n ) ] N = \begin{bmatrix}
N_{0,p}(t_0) & N_{1,p}(t_0) & \cdots & N_{n,p}(t_0) \\
N_{0,p}(t_1) & N_{1,p}(t_1) & \cdots & N_{n,p}(t_1) \\
\vdots & \vdots & \ddots & \vdots \\
N_{0,p}(t_n) & N_{1,p}(t_n) & \cdots & N_{n,p}(t_n)
\end{bmatrix}
N = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ N 0 , p ( t 0 ) N 0 , p ( t 1 ) ⋮ N 0 , p ( t n ) N 1 , p ( t 0 ) N 1 , p ( t 1 ) ⋮ N 1 , p ( t n ) ⋯ ⋯ ⋱ ⋯ N n , p ( t 0 ) N n , p ( t 1 ) ⋮ N n , p ( t n ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
我们将向量D k \mathbf{D}_k D k P i \mathbf{P}_i P i D \mathbf{D} D P \mathbf{P} P
D = [ d 01 d 02 d 03 ⋯ d 0 s d 11 d 12 d 13 ⋯ d 1 s ⋮ ⋱ ⋮ d n 1 d n 2 d n 3 ⋯ d n s ] P = [ p 01 p 02 p 03 ⋯ p 0 s p 11 p 12 p 13 ⋯ p 1 s ⋮ ⋱ ⋮ p n 1 p n 2 p n 3 ⋯ p n s ] \left.\mathbf{D}=\left[\begin{array}{ccccc}{d_{01}}&{d_{02}}&{d_{03}}&{\cdots}&{d_{0s}}\\{d_{11}}&{d_{12}}&{d_{13}}&{\cdots}&{d_{1s}}\\{\vdots}&&&{\ddots}&{\vdots}\\{d_{n1}}&{d_{n2}}&{d_{n3}}&{\cdots}&{d_{ns}}\end{array}\right.\right]\quad\mathbf{P}=\left[\begin{array}{ccccc}{p_{01}}&{p_{02}}&{p_{03}}&{\cdots}&{p_{0s}}\\{p_{11}}&{p_{12}}&{p_{13}}&{\cdots}&{p_{1s}}\\{\vdots}&&&{\ddots}&{\vdots}\\{p_{n1}}&{p_{n2}}&{p_{n3}}&{\cdots}&{p_{ns}}\end{array}\right]
D = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ d 0 1 d 1 1 ⋮ d n 1 d 0 2 d 1 2 d n 2 d 0 3 d 1 3 d n 3 ⋯ ⋯ ⋱ ⋯ d 0 s d 1 s ⋮ d n s ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ P = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ p 0 1 p 1 1 ⋮ p n 1 p 0 2 p 1 2 p n 2 p 0 3 p 1 3 p n 3 ⋯ ⋯ ⋱ ⋯ p 0 s p 1 s ⋮ p n s ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
D k \mathbf{D}_k D k s s s D k = [ d k 1 , … , d k s ] \mathbf{D}_k=[d_{k1}, \ldots, d_{ks}] D k = [ d k 1 , … , d k s ] D \mathbf{D} D k k k P i \mathbf{P}_i P i s s s P i = [ p i 1 , … , p i s ] \mathbf{P}_i = [p_{i1}, \ldots, p_{is}] P i = [ p i 1 , … , p i s ] s = 3 s=3 s = 3 s = 2 s=2 s = 2 D \mathbf{D} D P \mathbf{P} P ( n + 1 ) × s (n +1) \times s ( n + 1 ) × s D k \mathbf{D}_k D k t i t_i t i
D = N ⋅ P \mathbf{D} = \mathbf{N} \cdot \mathbf{P}
D = N ⋅ P
矩阵D \mathbf{D} D N \mathbf{N} N D \mathbf{D} D N \mathbf{N} N P \mathbf{P} P P \mathbf{P} P P \mathbf{P} P
D \mathbf{D} D i i i P \mathbf{P} P i i i D i \mathbf{D}_i D i P i \mathbf{P}_i P i
d i = N ⋅ p i \mathbf{d}^i = \mathbf{N} \cdot \mathbf{p}^i
d i = N ⋅ p i
根据N \mathbf{N} N d i \mathbf{d}^i d i p i \mathbf{p}^i p i 0 ≤ i ≤ h 0\leq i \leq h 0 ≤ i ≤ h i i i P \mathbf{P} P
但是,这是非常低效的。不过,许多数值计算库为我们提供了现成的线性系统求解器,能够有效地求解方程组D = N P \mathbf{D} = \mathbf{N}\mathbf{P} D = N P
下面是相关算法的步骤:
Input: n + 1 n+1 n + 1 D 0 \mathbf{D}_0 D 0 D n \mathbf{D}_n D n p p p Output: 次数为p p p
算法:
选择一种方式计算n + 1 n+1 n + 1 t 0 , . . . , t n t_0, ..., t_n t 0 , . . . , t n U U U for i i i 0 0 0 to n n n do for j j j 0 0 0 to n n n do N \mathbf{N} N i i i j j j N j , p ( t i ) N_{j,p}(t_i) N j , p ( t i )
for i i i 0 0 0 to n n n do D i \mathbf{D}_i D i D \mathbf{D} D i i i
使用线性方程求解器求解D = N P \mathbf{D} = \mathbf{N}\mathbf{P} D = N P P \mathbf{P} P P \mathbf{P} P i i i P i \mathbf{P}_i P i P 0 \mathbf{P}_0 P 0 P n \mathbf{P}_n P n U U U p p p
下面左图是一个例子。有9个给定数据点(黑色表示),蓝色点为计算出的控制点。插值曲线上的蓝点小圆点是使用弦长法计算出的节点。可以看出,这些“节点”非常接近数据点,控制多边形也紧贴着数据点连成的多边形。但并不是所有的时候都会如此,下图右图中,数据点连成的多边形和控制多边则形非常不同。
如果通过对连续p p p N \mathbf{N} N p p p ∣ i − k ∣ ≥ p |i - k| \geq p ∣ i − k ∣ ≥ p N i , p ( t k ) = 0 N_{i,p}(t_k) = 0 N i , p ( t k ) = 0 这意味着通过这样的参数化算法得到的线性方程组可以使用高斯消元法求解。
一般来说,所选参数和节点对结果曲线的影响是无法预测的,**但是,如果弦长分布大致相同,那么四种参数化方法生成的曲线应该相似。**此外,通用参数化方法应该与均匀参数化方法表现相似,因为当节点均匀分布时,B样条基函数的最大值分布是均匀的。但是,当弦长分布剧烈变化时,四种参数选择方式产生的曲线则会大不相同。
下图中的四条曲线是使用四种参数化方法获得的,插值B样条曲线的次数为3。均匀参数化产生了一个尖点,弦长参数化生成的曲线在数据点之间会有较大的波动,向心参数化类似于弦长参数化但表现更好,通用参数化方法紧贴着数据点连成的多边形(比均匀参数化更好),但产生了一个小的环。
参数和节点之间的关系如何?下图显示了所有四种方法的参数和节点分布。通用参数化方法获得的参数和节点比弦长参数化和向心参数化的分布更均匀。弦长参数化获得的较长曲线段在向心参数化中会变短,曲线也不会在数据点之间剧烈摆动。
次数对插值B样条曲线形状的影响也很难预测。可以从下图中观察到,均匀参数化和通用参数化法通常很好地跟踪长弦,但是,它们在短弦上会出现问题。由于参数间距几乎相等,因此对于较短的弦,插值曲线会拉伸得更长一些。因此,我们会看到峰值和自交环。当次数增加时,这种情况会变得更加明显,因为高阶曲线提供了更多的摆动自由度。
均匀法
弦长法
向心法
通用方法
2阶
3阶
4阶
5阶
对于弦长参数化,上图显示它对长弦的效果不是很好,特别是后面或前面有一些较短的弦,可能会发生大的凸起。次数对上图中显示的插值曲线形状没有显著影响。由于向心参数化是弦长参数化的扩展,因此两者具有相同的特点。然而,向心参数化会降低两个相邻参数之间距离之差的影响,它也具有均匀参数化和通用参数化方法相似的特点。例如,生成的插值曲线会紧贴着较长的弦,当次数增加时,短弦处可能会出现自交环。
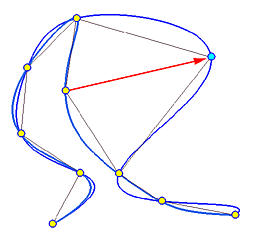
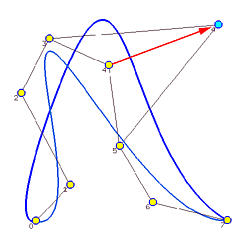
即使使用满足局部修改特性的B样条曲线,这种插值方法也是全局的 ,因为改变单个数据点的位置会完全改变插值曲线的形状。下图中,黄色点是数据点,其中一个被移动到新位置,以浅蓝色标记,并用红色箭头指示。这九个数据点使用4次B样条曲线采用向心参数化插值得到。
可以看到,移动数据点后的插值曲线(蓝色)和原始曲线有八个数据点是相同的,但八个曲线段都不完全相同,因此,改变单个数据点的位置会全局地改变插值曲线的形状!
在插值中,插值曲线会按照顺序通过所有给定的数据点,曲线可能会在数据点之间疯狂摆动,而不是紧贴着数据点连成的多边形。曲线逼近则是放宽了要求,不严格要求曲线必须经过所有点。在全局逼近中,除了第一个和最后一个数据点之外,曲线不必经过每一个点。
为了衡量一条曲线“逼近”给定数据点连成的多边形的程度,提出了 误差距离的概念。
误差距离是数据点与其在曲线上的对应点之间的距离 。因此,如果这些误差距离的总和最小,曲线就会紧贴数据点连成的多边形。插值曲线就是一种特殊结果,因为每个数据点的误差距离为零,以这种方式获得的曲线称为逼近曲线 。
假设我们有n + 1 n+1 n + 1 D 0 , D 1 , . . . , D n \mathbf{D}_0, \mathbf{D}_1, ..., \mathbf{D}_n D 0 , D 1 , . . . , D n h + 1 h+1 h + 1 p p p n > h ≥ p ≥ 1 n > h \geq p \geq 1 n > h ≥ p ≥ 1
全局曲线逼近 :给定一组n + 1 n+1 n + 1 D 0 , D 1 , . . . , D n \mathbf{D}_0, \mathbf{D}_1, ..., \mathbf{D}_n D 0 , D 1 , . . . , D n n > h ≥ p ≥ 1 n > h \geq p \geq 1 n > h ≥ p ≥ 1
这条曲线经过第一个点和最后一个点(即D 0 \mathbf{D}_0 D 0 D n \mathbf{D}_n D n 这条曲线上各个点的误差距离之和最小。
有了 h h h p p p t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n
C ( u ) = ∑ i = 0 h N i , p ( u ) P i C(u) = \sum_{i=0}^{h} N_{i,p}(u)P_i
C ( u ) = i = 0 ∑ h N i , p ( u ) P i
其中 P 0 , P 1 , . . . , P h \mathbf{P}_0, \mathbf{P}_1, ..., \mathbf{P}_h P 0 , P 1 , . . . , P h h + 1 h+1 h + 1 D 0 = C ( 0 ) = P 0 \mathbf{D}_0 = \mathbf{C}(0) = \mathbf{P}_0 D 0 = C ( 0 ) = P 0 D n = C ( 1 ) = P h \mathbf{D}_n = \mathbf{C}(1) = \mathbf{P}_h D n = C ( 1 ) = P h h − 1 h-1 h − 1 P 1 , P 2 , . . . , P h − 1 \mathbf{P}_1, \mathbf{P}_2, ..., \mathbf{P}_{h-1} P 1 , P 2 , . . . , P h − 1
C ( u ) = N 0 , p ( u ) D 0 + ( ∑ i = 1 h − 1 N i , p ( u ) P i ) + N h , p ( u ) D n \mathbf{C}(u)=N_{0,p}(u)\mathbf{D}_{0}+\left(\sum_{i=1}^{h-1}N_{i,p}(u)\mathbf{P}_{i}\right)+N_{h,p}(u)\mathbf{D}_{n}
C ( u ) = N 0 , p ( u ) D 0 + ( i = 1 ∑ h − 1 N i , p ( u ) P i ) + N h , p ( u ) D n
如何测量误差距离?
参数 t k t_k t k D k \mathbf{D}_k D k D k \mathbf{D}_k D k t k t_k t k ∣ D k − C ( t k ) ∣ |\mathbf{D}_k - \mathbf{C}(t_k) | ∣ D k − C ( t k ) ∣ ∣ D k − C ( t k ) ∣ 2 |\mathbf{D}_k - \mathbf{C}(t_k) |^2 ∣ D k − C ( t k ) ∣ 2
因此,所有平方误差距离之和是:
f ( P 1 , … , P h − 1 ) = ∑ k = 1 n − 1 ∣ D k − C ( t k ) ∣ 2 f(P_1, \ldots, P_{h-1}) = \sum_{k=1}^{n-1} | \mathbf{D}_k - C(t_k) |^2
f ( P 1 , … , P h − 1 ) = k = 1 ∑ n − 1 ∣ D k − C ( t k ) ∣ 2
我们的目标是找到一些控制点 P 1 , . . . , P h − 1 \mathbf{P}_1, ..., \mathbf{P}_{h-1} P 1 , . . . , P h − 1 f ( ) f() f ( )
我们将D k − C ( t k ) \mathbf{D}_k - \mathbf{C}(t_k) D k − C ( t k )
D k − C ( t k ) = D k − [ N 0 , p ( t k ) D 0 + ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) + N h , p ( t k ) D n ] = ( D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D n ) − ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) \begin{aligned}\mathbf{D}_{k}-\mathbf{C}(t_{k})&=\quad\mathbf{D}_k-\left[N_{0,p}(t_k)\mathbf{D}_0+\left(\sum_{i=1}^{h-1}N_{i,p}(t_k)\mathbf{P}_i\right)+N_{h,p}(t_k)\mathbf{D}_n\right]\\&=\quad(\mathbf{D}_k-N_{0,p}(t_k)\mathbf{D}_0-N_{h,p}(t_k)\mathbf{D}_n)-\left(\sum_{i=1}^{h-1}N_{i,p}(t_k)\mathbf{P}_i\right)\end{aligned}
D k − C ( t k ) = D k − [ N 0 , p ( t k ) D 0 + ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) + N h , p ( t k ) D n ] = ( D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D n ) − ( i = 1 ∑ h − 1 N i , p ( t k ) P i )
在上面的公式中,D 0 \mathbf{D}_0 D 0 D k \mathbf{D}_k D k D n \mathbf{D}_n D n N 0 , p ( t k ) N_{0,p}(t_k) N 0 , p ( t k ) N h , p ( t k ) N_{h,p}(t_k) N h , p ( t k ) N 0 , p ( u ) N_{0,p}(u) N 0 , p ( u ) N h , p ( u ) N_{h,p}(u) N h , p ( u ) t k t_k t k Q k \mathbf{Q}_k Q k
Q k = D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D h \mathbf{Q}_k = \mathbf{D}_k - N_{0,p}(t_k)\mathbf{D}_0 - N_{h,p}(t_k)\mathbf{D}_h
Q k = D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D h
然后,误差距离平方和函数 f ( ) f() f ( )
f ( P 1 , … , P h − 1 ) = ∑ k = 1 n − 1 ∣ Q k − ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ∣ 2 f(\mathbf{P}_1,\ldots,\mathbf{P}_{h-1})=\sum_{k=1}^{n-1}\left|\mathbf{Q}_k-\left(\sum_{i=1}^{h-1}N_{i,p}(t_k)\mathbf{P}_i\right)\right|^2
f ( P 1 , … , P h − 1 ) = k = 1 ∑ n − 1 ∣ ∣ ∣ ∣ ∣ ∣ Q k − ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ∣ ∣ ∣ ∣ ∣ ∣ 2
回想一下恒等式 x ⋅ x = ∣ x ∣ 2 \mathbf{x} · \mathbf{x} = | \mathbf{x} |^2 x ⋅ x = ∣ x ∣ 2 x \mathbf{x} x x \mathbf{x} x
∣ Q k − ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ∣ 2 = ( Q k − ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ) ⋅ ( Q k − ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ) = Q k ⋅ Q k − 2 ( ∑ i = 1 h − 1 N i , p ( t k ) P i ⋅ Q k ) + ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) \begin{aligned}
&\left|\mathbf{Q}_{k}-\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\right|^{2} \\
&=\left(\mathbf{Q}_{k}-\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\right)\cdot\left(\mathbf{Q}_{k}-\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\right) \\
&=\mathbf{Q}_{k}\cdot\mathbf{Q}_{k}-2\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\cdot\mathbf{Q}_{k}\right)+\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)
\end{aligned}
∣ ∣ ∣ ∣ ∣ ∣ Q k − ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ∣ ∣ ∣ ∣ ∣ ∣ 2 = ( Q k − ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ) ⋅ ( Q k − ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ) = Q k ⋅ Q k − 2 ( i = 1 ∑ h − 1 N i , p ( t k ) P i ⋅ Q k ) + ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) P i )
因此,函数f f f
f ( P 1 , … , P h − 1 ) = ∑ k = 1 n − 1 [ Q k ⋅ Q k − 2 ( ∑ i = 1 h − 1 N i , p ( t k ) P i ⋅ Q k ) + ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ] \begin{aligned}
f(\mathbf{P}_{1},\ldots,\mathbf{P}_{h-1})&=\sum_{k=1}^{n-1}\left[\mathbf{Q}_{k}\cdot\mathbf{Q}_{k}-2\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\cdot\mathbf{Q}_{k}\right)\right.\\
&\quad\left.+\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\right]
\end{aligned}
f ( P 1 , … , P h − 1 ) = k = 1 ∑ n − 1 [ Q k ⋅ Q k − 2 ( i = 1 ∑ h − 1 N i , p ( t k ) P i ⋅ Q k ) + ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ]
让函数f f f P g \mathbf{P}_{g} P g f f f
在计算函数f f f P g \mathbf{P}_{g} P g Q k \mathbf{Q}_k Q k N i , p ( t k ) N_{i,p}(t_k) N i , p ( t k ) P g \mathbf{P}_{g} P g
∂ ∂ P g ( Q k ⋅ Q k ) = 0 \frac{\partial}{\partial\mathbf{P}_{g}}\left(\mathbf{Q}_{k}\cdot\mathbf{Q}_{k}\right)=0
∂ P g ∂ ( Q k ⋅ Q k ) = 0
考虑求和中的第二项,即 N i , p ( t k ) P i Q k N_{i,p}(t_k) \mathbf{P}_i \mathbf{Q}_k N i , p ( t k ) P i Q k
∂ ∂ P g ( N i , p ( t k ) P i ⋅ Q k ) = N i , p ( t k ) ∂ P i ∂ P g ⋅ Q k \frac{\partial}{\partial\mathbf{P}_{g}}\left(N_{i,p}(t_{k})\mathbf{P}_{i}\cdot\mathbf{Q}_{k}\right)=N_{i,p}(t_{k})\frac{\partial\mathbf{P}_{i}}{\partial\mathbf{P}_{g}}\cdot\mathbf{Q}_{k}
∂ P g ∂ ( N i , p ( t k ) P i ⋅ Q k ) = N i , p ( t k ) ∂ P g ∂ P i ⋅ Q k
P i \mathbf{P}_i P i P g \mathbf{P}_{g} P g i = g i = g i = g
∂ ∂ P g ( ∑ i = 1 h − 1 N i , p ( t k ) P i ⋅ Q k ) = N g , p ( t k ) Q k \frac{\partial}{\partial\mathbf{P}_{g}}\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\cdot\mathbf{Q}_{k}\right)=N_{g,p}(t_{k})\mathbf{Q}_{k}
∂ P g ∂ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ⋅ Q k ) = N g , p ( t k ) Q k
第三项的偏导数比较复杂,需要用到求导规则 ( f . g ) ′ = f ′ . g + f . g ′ (f.g)' = f'.g + f.g' ( f . g ) ′ = f ′ . g + f . g ′
∂ ∂ P g ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) = ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) ∂ P i ∂ P g ) + ( ∑ i = 1 h − 1 N i , p ( t k ) ∂ P i ∂ P g ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) = 2 ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) ∂ P i ∂ P g ) \begin{gathered}
{\frac{\partial}{\partial\mathbf{P}_{g}}}\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right) \\
=\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\frac{\partial\mathbf{P}_{i}}{\partial\mathbf{P}_{g}}\right)+\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\frac{\partial\mathbf{P}_{i}}{\partial\mathbf{P}_{g}}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right) \\
=2\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\frac{\partial\mathbf{P}_{i}}{\partial\mathbf{P}_{g}}\right)
\end{gathered}
∂ P g ∂ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) = ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) ∂ P g ∂ P i ) + ( i = 1 ∑ h − 1 N i , p ( t k ) ∂ P g ∂ P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) = 2 ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) ∂ P g ∂ P i )
由于P i \mathbf{P}_i P i P g \mathbf{P}_{g} P g i i i g g g P g \mathbf{P}_{g} P g
∂ ∂ P g ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) ⋅ ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) = 2 N g , p ( t k ) ( ∑ i = 1 h − 1 N i , p ( t k ) P i ) \frac{\partial}{\partial\mathbf{P}_{g}}\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)\cdot\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)=2N_{g,p}(t_{k})\left(\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}\right)
∂ P g ∂ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) ⋅ ( i = 1 ∑ h − 1 N i , p ( t k ) P i ) = 2 N g , p ( t k ) ( i = 1 ∑ h − 1 N i , p ( t k ) P i )
综上,函数 f ( ) f() f ( ) P g \mathbf{P}_{g} P g
∂ f ∂ P g = − 2 N g , p ( t k ) Q k + 2 N g , p ( t k ) ∑ i = 1 h − 1 N i , p ( t k ) P i \frac{\partial f}{\partial\mathbf{P}_{g}}=-2N_{g,p}(t_{k})\mathbf{Q}_{k}+2N_{g,p}(t_{k})\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}
∂ P g ∂ f = − 2 N g , p ( t k ) Q k + 2 N g , p ( t k ) i = 1 ∑ h − 1 N i , p ( t k ) P i
令其等于零,我们得到:
∑ k = 1 n − 1 N g , p ( t k ) ∑ i = 1 h − 1 N i , p ( t k ) P i = ∑ k = 1 n − 1 N g , p ( t k ) Q k \sum_{k=1}^{n-1}N_{g,p}(t_k)\sum_{i=1}^{h-1}N_{i,p}(t_k)\mathbf{P}_i=\sum_{k=1}^{n-1}N_{g,p}(t_k)\mathbf{Q}_k
k = 1 ∑ n − 1 N g , p ( t k ) i = 1 ∑ h − 1 N i , p ( t k ) P i = k = 1 ∑ n − 1 N g , p ( t k ) Q k
由于我们有 h − 1 h-1 h − 1 g g g h − 1 h-1 h − 1 h − 1 h-1 h − 1
我们定义以下三个矩阵:
P = [ P 1 P 2 ⋮ P h − 1 ] Q = [ ∑ k = 1 n − 1 N 1 , p ( t k ) Q k ∑ k = 1 n − 1 N 2 , p ( t k ) Q k ⋮ ∑ k = 1 n − 1 N h − 1 , p ( t k ) Q k ] \left.\mathbf{P}=\left[\begin{array}{c}\mathbf{P}_1\\\mathbf{P}_2\\\vdots\\\mathbf{P}_{h-1}\end{array}\right.\right]\quad\mathbf{Q}=\left[\begin{array}{c}\sum_{k=1}^{n-1}N_{1,p}(t_k)\mathbf{Q}_k\\\sum_{k=1}^{n-1}N_{2,p}(t_k)\mathbf{Q}_k\\\vdots\\\sum_{k=1}^{n-1}N_{h-1,p}(t_k)\mathbf{Q}_k\end{array}\right]
P = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ P 1 P 2 ⋮ P h − 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ Q = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ∑ k = 1 n − 1 N 1 , p ( t k ) Q k ∑ k = 1 n − 1 N 2 , p ( t k ) Q k ⋮ ∑ k = 1 n − 1 N h − 1 , p ( t k ) Q k ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
N = [ N 1 , p ( t 1 ) N 2 , p ( t 1 ) ⋯ N h − 1 , p ( t 1 ) N 1 , p ( t 2 ) N 2 , p ( t 2 ) ⋯ N h − 1 , p ( t 2 ) ⋮ ⋱ ⋮ N 1 , p ( t n − 1 ) N 2 , p ( t n − 1 ) ⋯ N h − 1 , p ( t n − 1 ) ] \mathbf{N}=\left[\begin{array}{cccc}N_{1,p}(t_1)&N_{2,p}(t_1)&\cdots&N_{h-1,p}(t_1)\\N_{1,p}(t_2)&N_{2,p}(t_2)&\cdots&N_{h-1,p}(t_2)\\\vdots&&\ddots&\vdots\\N_{1,p}(t_{n-1})&N_{2,p}(t_{n-1})&\cdots&N_{h-1,p}(t_{n-1})\end{array}\right]
N = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ N 1 , p ( t 1 ) N 1 , p ( t 2 ) ⋮ N 1 , p ( t n − 1 ) N 2 , p ( t 1 ) N 2 , p ( t 2 ) N 2 , p ( t n − 1 ) ⋯ ⋯ ⋱ ⋯ N h − 1 , p ( t 1 ) N h − 1 , p ( t 2 ) ⋮ N h − 1 , p ( t n − 1 ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
在这里,P \mathbf{P} P k k k P k \mathbf{P}_k P k Q \mathbf{Q} Q k k k k k k N \mathbf{N} N k k k N 1 , p ( u ) , N 2 , p ( u ) , . . . , N h − 1 , p ( u ) N_{1,p}(u), N_{2,p}(u), ..., N_{h-1,p}(u) N 1 , p ( u ) , N 2 , p ( u ) , . . . , N h − 1 , p ( u ) t k t_k t k s s s P \mathbf{P} P N \mathbf{N} N Q \mathbf{Q} Q ( h − 1 ) × s (h-1)×s ( h − 1 ) × s
现在,让我们重写第 g g g
∑ k = 1 n − 1 N g , p ( t k ) ∑ i = 1 h − 1 N i , p ( t k ) P i = ∑ k = 1 n − 1 N g , p ( t k ) Q k \sum_{k=1}^{n-1}N_{g,p}(t_{k})\sum_{i=1}^{h-1}N_{i,p}(t_{k})\mathbf{P}_{i}=\sum_{k=1}^{n-1}N_{g,p}(t_{k})\mathbf{Q}_{k}
k = 1 ∑ n − 1 N g , p ( t k ) i = 1 ∑ h − 1 N i , p ( t k ) P i = k = 1 ∑ n − 1 N g , p ( t k ) Q k
换一种形式,以便可以看出 P i \mathbf{P}_i P i
∑ i = 1 h − 1 ( ∑ k = 1 n − 1 N g , p ( t k ) N i , p ( t k ) ) P i = ∑ k = 1 n − 1 N g , p ( t k ) Q k \sum_{i=1}^{h-1}\left(\sum_{k=1}^{n-1}N_{g,p}(t_k)N_{i,p}(t_k)\right)\mathbf{P}_i=\sum_{k=1}^{n-1}N_{g,p}(t_k)\mathbf{Q}_k
i = 1 ∑ h − 1 ( k = 1 ∑ n − 1 N g , p ( t k ) N i , p ( t k ) ) P i = k = 1 ∑ n − 1 N g , p ( t k ) Q k
最后,P i \mathbf{P}_i P i
∑ k = 1 n − 1 N g , p ( t k ) N i , p ( t k ) \begin{aligned}\sum_{k=1}^{n-1}N_{g,p}(t_k)N_{i,p}(t_k)\end{aligned}
k = 1 ∑ n − 1 N g , p ( t k ) N i , p ( t k )
如果观察矩阵 N \mathbf{N} N N g , p ( t 1 ) , N g , p ( t 2 ) , . . . , N g , p ( t n − 1 ) N_{g,p}(t_1), N_{g,p}(t_2), ..., N_{g,p}(t_{n-1}) N g , p ( t 1 ) , N g , p ( t 2 ) , . . . , N g , p ( t n − 1 ) N \mathbf{N} N g g g N i , p ( t 1 ) , N i , p ( t 2 ) , . . . , N i , p ( t n − 1 ) N_{i,p}(t_1), N_{i,p}(t_2), ..., N_{i,p}(t_{n-1}) N i , p ( t 1 ) , N i , p ( t 2 ) , . . . , N i , p ( t n − 1 ) N \mathbf{N} N i i i N \mathbf{N} N g g g N \mathbf{N} N N T \mathbf{N}^T N T g g g P i \mathbf{P}_i P i N \mathbf{N} N g g g N \mathbf{N} N i i i
( N T N ) P = Q \begin{pmatrix}\mathrm{N}^T\mathrm{N}\end{pmatrix}\mathrm{P}=\mathrm{Q}
( N T N ) P = Q
由于 N \mathbf{N} N Q \mathbf{Q} Q P \mathbf{P} P
Input: n + 1 n+1 n + 1 D 0 \mathbf{D}_0 D 0 D 1 \mathbf{D}_1 D 1 D n \mathbf{D}_n D n p p p h + 1 h+1 h + 1 Output: 一条由h + 1 h+1 h + 1 p p p
算法:
计算一组参数t 0 , . . . , t n t_0, ..., t_n t 0 , . . . , t n U U U P 0 = D 0 \mathbf{P}_0=\mathbf{D}_0 P 0 = D 0 P h = D n \mathbf{P}_h=\mathbf{D}_n P h = D n for k k k 1 1 1 to n − 1 n-1 n − 1 do Q k \mathbf{Q}_k Q k Q k = D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D n \mathbf{Q}_{k}=\mathbf{D}_{k}-N_{0,p}(t_{k})\mathbf{D}_{0}-N_{h,p}(t_{k})\mathbf{D}_{n} Q k = D k − N 0 , p ( t k ) D 0 − N h , p ( t k ) D n for i i i 1 1 1 to h − 1 h-1 h − 1 do Q \mathbf{Q} Q i i i ∑ k = 1 n − 1 N i , p ( t k ) Q k \sum_{k=1}^{n-1}N_{i,p}(t_k)\mathbf{Q}_k ∑ k = 1 n − 1 N i , p ( t k ) Q k Q \mathbf{Q} Q
for k k k 1 1 1 to n − 1 n-1 n − 1 do for i i i 1 1 1 to h − 1 h-1 h − 1 do N i , p ( t k ) N_{i,p}(t_k) N i , p ( t k ) N \mathbf{N} N k k k i i i N \mathbf{N} N M = N T N \mathbf{M} = \mathbf{N}^T \mathbf{N} M = N T N M ⋅ P = Q \mathbf{M} \cdot \mathbf{P} = \mathbf{Q} M ⋅ P = Q P \mathbf{P} P P \mathbf{P} P i i i P i \mathbf{P}_i P i P 0 \mathbf{P}_0 P 0 P h \mathbf{P}_h P h U U U p p p
显然,数据点数量会影响逼近曲线的形状。那么次数 p p p
控制点数量=4 控制点数量=5 控制点数量=6 控制点数量=7
次数=2
次数=3
次数=4
次数=5
可以看出,通常次数较低的曲线无法很好地逼近数据点连成的多边形,而较高次数的曲线结果更好(更接近数据多边形)。类似地,控制点越多,逼近曲线的灵活性就越高。因此,在每一行中,随着控制点数量的增加,曲线更接近数据点连成的多边形。
那是否应该使用高阶曲线和更多的控制点?答案是不,因为全局逼近只需要比全局插值更少的控制点 。如果控制点的数量等于数据点的数量,全局逼近就变成了全局插值 ,我们可以直接使用全局插值!至于次数,只要生成的曲线能够接近数据多边形的形状,我们希望次数尽可能的小。
这种逼近方法是全局的,因为改变一个数据点的位置会导致整个曲线发生变化。下图中的黄点是给定的数据点,用一条由5个控制点定义的3次B样条曲线(n = 7 , p = 3 n = 7, p=3 n = 7 , p = 3 h = 4 h = 4 h = 4
如图所示,除了经过第一个和最后一个数据点外,原始曲线和新曲线的形状截然不同,因此,修改数据点引起的变化是全局的!
得到一组参数后,我们就可以计算节点向量,参数点相当于控制点。假设我们有n + 1 n+1 n + 1 t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n p p p p p p m + 1 m+1 m + 1 m m m m = n + p + 1 m = n + p + 1 m = n + p + 1
u 0 = u 1 = . . . = u p = 0 , u p + 1 , . . . , u m − p − 1 , u m − p = u m − p + 1 = . . . = u m = 1. u_0 = u_1 = ... = u_p = 0, u_{p+1}, ..., u_{m-p-1}, u_{m-p} = u_{m-p+1} = ... = u_m = 1. u 0 = u 1 = . . . = u p = 0 , u p + 1 , . . . , u m − p − 1 , u m − p = u m − p + 1 = . . . = u m = 1 .
前 p + 1 p+1 p + 1 p + 1 p+1 p + 1 n − p n-p n − p n − p n-p n − p u p = 0 , u p + 1 , . . . , u m − p − 1 , u m − p = 1 u_p = 0, u_{p+1}, ..., u_{m-p-1}, u_{m-p} = 1 u p = 0 , u p + 1 , . . . , u m − p − 1 , u m − p = 1 [ 0 , 1 ] [0,1] [ 0 , 1 ] n − p + 1 n-p+1 n − p + 1
u 0 = u 1 = ⋯ = u p = 0 u j + p = j n − p + 1 f o r j = 1 , 2 , … , n − p u m − p = u m − p + 1 = ⋯ = u m = 1 \begin{aligned}u_{0}&=\quad u_1=\cdots=u_p=0\\u_{j+p}&=\quad\frac j{n-p+1}\quad\mathrm{for~}j=1,2,\ldots,n-p\\u_{m-p}&=\quad u_{m-p+1}=\cdots=u_m=1\end{aligned}
u 0 u j + p u m − p = u 1 = ⋯ = u p = 0 = n − p + 1 j f o r j = 1 , 2 , … , n − p = u m − p + 1 = ⋯ = u m = 1
例如,如果我们有6个(n = 5 n = 5 n = 5 p = 3 p = 3 p = 3 ( n + p + 1 ) + 1 = ( 5 + 3 + 1 ) + 1 = 10 (n + p + 1) + 1 = (5 + 3 + 1) + 1 = 10 ( n + p + 1 ) + 1 = ( 5 + 3 + 1 ) + 1 = 1 0 m = 9 m = 9 m = 9 p + 1 p + 1 p + 1 u 4 u_4 u 4 u 5 u_5 u 5 u 4 , u 5 u_4,u_5 u 4 , u 5 [ 0 , 1 ] [0,1] [ 0 , 1 ]
{ 0 , 0 , 0 , 0 , 1 3 , 2 3 , 1 , 1 , 1 , 1 } . \{0, 0, 0, 0, \frac{1}{3}, \frac{2}{3}, 1, 1, 1, 1\}.
{ 0 , 0 , 0 , 0 , 3 1 , 3 2 , 1 , 1 , 1 , 1 } .
均匀分布的节点向量计算起来非常简单,不过,不推荐使用这种方法,因为如果采用弦长参数化得到参数,并使用均匀分布法计算节点,那么最后得到的线性方程组是奇异的。
另一种计算节点向量的方法是由de Boor提出,即平均参数法 ,计算公式如下:
u 0 = u 1 = ⋯ = u p = 0 u j + p = 1 p ∑ i = j j + p − 1 t i for j = 1 , 2 , … , n − p u m − p = u m − p + 1 = ⋯ = u m = 1 \begin{aligned}u_{0}&=\quad u_1=\cdots=u_p=0\\u_{j+p}&=\quad\frac1p\sum_{i=j}^{j+p-1}t_i\quad\text{for }j=1,2,\ldots,n-p\\u_{m-p}&=\quad u_{m-p+1}=\cdots=u_m=1\end{aligned}
u 0 u j + p u m − p = u 1 = ⋯ = u p = 0 = p 1 i = j ∑ j + p − 1 t i for j = 1 , 2 , … , n − p = u m − p + 1 = ⋯ = u m = 1
因此,第一个内部节点是 p p p t 1 , t 2 , . . . , t p t_1, t_2, ..., t_p t 1 , t 2 , . . . , t p p p p t 2 , t 3 , . . . , t p + 1 t_2, t_3, ..., t_{p+1} t 2 , t 3 , . . . , t p + 1 n = 5 n = 5 n = 5
t 0 t 1 t 2 t 3 t 4 t 5 0 1 4 1 3 2 3 3 4 1 \begin{array}{|c|c|c|c|c|c|c|}
\hline
t_0 & t_1 & t_2 & t_3 & t_4 & t_5 \\
\hline
0 & \frac{1}{4} & \frac{1}{3} & \frac{2}{3} & \frac{3}{4} & 1 \\
\hline
\end{array}
t 0 0 t 1 4 1 t 2 3 1 t 3 3 2 t 4 4 3 t 5 1
假设我们要计算一个次数为3 3 3 m = 9 m = 9 m = 9 1 4 , 1 3 , 2 3 \frac{1}{4}, \frac{1}{3}, \frac{2}{3} 4 1 , 3 1 , 3 2 1 3 , 2 3 , 3 4 \frac{1}{3}, \frac{2}{3}, \frac{3}{4} 3 1 , 3 2 , 4 3
u 0 = u 1 = . . . = u 2 = u 3 u 4 u 5 u 6 = u 7 = . . . = u 8 = u 9 0 1 4 + 1 3 + 2 3 / 3 = 5 12 1 3 + 2 3 + 3 4 / 3 = 7 12 1 \begin{array}{|c|c|c|c|c|}
\hline
u_0 = u_1 = ... = u_2 = u_3 & u_4 & u_5 & u_6 = u_7 = ... = u_8 = u_9 \\
\hline
0 & \frac{1}{4} + \frac{1}{3} + \frac{2}{3} / 3 = \frac{5}{12} & \frac{1}{3} + \frac{2}{3} + \frac{3}{4} / 3 = \frac{7}{12} & 1 \\
\hline
\end{array}
u 0 = u 1 = . . . = u 2 = u 3 0 u 4 4 1 + 3 1 + 3 2 / 3 = 1 2 5 u 5 3 1 + 3 2 + 4 3 / 3 = 1 2 7 u 6 = u 7 = . . . = u 8 = u 9 1
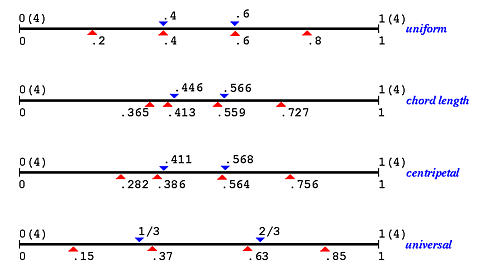
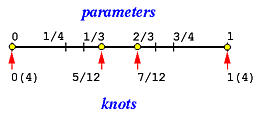
下图说明了参数的位置和得到的节点位置。注意0 ( 4 ) 0(4) 0 ( 4 ) 1 ( 4 ) 1(4) 1 ( 4 ) 0 0 0 1 1 1 [ 0 , 5 12 ) [0, \frac{5}{12}) [ 0 , 1 2 5 ) [ 5 12 , 7 12 ) [\frac{5}{12}, \frac{7}{12}) [ 1 2 5 , 1 2 7 ) [ 7 12 , 1 ) [\frac{7}{12}, 1) [ 1 2 7 , 1 )
假设我们有m + 1 m+1 m + 1 n + 1 n+1 n + 1 D i j \mathbf{D}_{ij} D i j 0 ≤ i ≤ m 0 \leq i \leq m 0 ≤ i ≤ m 0 ≤ j ≤ n 0 \leq j \leq n 0 ≤ j ≤ n ( p , q ) (p, q) ( p , q ) p p p q q q U \mathbf{U} U V \mathbf{V} V ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 )
之前在 曲面参数化和节点向量计算 中讨论过,我们可以计算出 u u u v v v s c s_c s c 0 ≤ c ≤ m 0 \leq c \leq m 0 ≤ c ≤ m t d t_d t d 0 ≤ d ≤ n 0 \leq d \leq n 0 ≤ d ≤ n u u u v v v U \mathbf{U} U V \mathbf{V} V
全局曲面插值:给定一个由( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) D i j \mathbf{D}_{ij} D i j (0 ≤ i ≤ m 0 \leq i \leq m 0 ≤ i ≤ m 0 ≤ j ≤ n 0 \leq j \leq n 0 ≤ j ≤ n ( p , q ) (p, q) ( p , q ) ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) ( p , q ) (p, q) ( p , q )
设B样条曲面定义如下:
S ( u , v ) = ∑ i = 0 m ∑ j = 0 n N i , p ( u ) N j , q ( v ) P i j S(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,p}(u)N_{j,q}(v)P_{ij}
S ( u , v ) = i = 0 ∑ m j = 0 ∑ n N i , p ( u ) N j , q ( v ) P i j
由于它经过所有数据点,并且参数 s c s_c s c t d t_d t d D c d \mathbf{D}_{cd} D c d u = s c u = s_c u = s c v = t d v = t_d v = t d
D c d = S ( s c , t d ) = ∑ i = 0 m ∑ j = 0 n N i , p ( s c ) N j , q ( t d ) P i j D_{cd} = S(s_c, t_d) = \sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,p}(s_c)N_{j,q}(t_d)P_{ij}
D c d = S ( s c , t d ) = i = 0 ∑ m j = 0 ∑ n N i , p ( s c ) N j , q ( t d ) P i j
由于N i , p ( s c ) N_{i,p}(s_c) N i , p ( s c ) j j j j j j
D c d = S ( s c , t d ) = ∑ i = 0 m ∑ j = 0 n N i , p ( s c ) N j , q ( t d ) P i j = ∑ i = 0 m N i , p ( s c ) ( ∑ j = 0 n N j , q ( t d ) P i j ) \begin{aligned}\mathbf{D}_{cd}&=\mathbf{S}(s_{c},t_{d})=\sum_{i=0}^{m}\sum_{j=0}^{n}N_{i,p}(s_{c})N_{j,q}(t_{d})\mathbf{P}_{ij}\\&=\sum_{i=0}^{m}N_{i,p}(s_{c})\left(\sum_{j=0}^{n}N_{j,q}(t_{d})\mathbf{P}_{ij}\right)\end{aligned}
D c d = S ( s c , t d ) = i = 0 ∑ m j = 0 ∑ n N i , p ( s c ) N j , q ( t d ) P i j = i = 0 ∑ m N i , p ( s c ) ( j = 0 ∑ n N j , q ( t d ) P i j )
我们发现索引 i i i P i j \mathbf{P}_{ij} P i j
Q i d = ∑ j = 0 n N j , q ( t d ) P i j \mathbf{Q}_{id}=\sum_{j=0}^nN_{j,q}(t_d)\mathbf{P}_{ij}
Q i d = j = 0 ∑ n N j , q ( t d ) P i j
准确地说,如果 i i i Q i d \mathbf{Q}_{id} Q i d q q q q q q t d t_d t d P \mathbf{P} P i i i n + 1 n+1 n + 1 未知控制点 (即,P i 0 \mathbf{P}_{i0} P i 0 P i 1 \mathbf{P}_{i1} P i 1 P i n \mathbf{P}_{in} P i n Q i d \mathbf{Q}_{id} Q i d D c d \mathbf{D}_{cd} D c d
D c d = ∑ i = 0 m N i , p ( s c ) Q i d D_{cd} = \sum_{i=0}^{m} N_{i,p}(s_c) Q_{id}
D c d = i = 0 ∑ m N i , p ( s c ) Q i d
因此,数据点D c d \mathbf{D}_{cd} D c d p p p p p p s c s_c s c Q \mathbf{Q} Q d d d m + 1 m+1 m + 1 未知控制点 (即,Q 0 d \mathbf{Q}_{0d} Q 0 d Q 1 d \mathbf{Q}_{1d} Q 1 d Q m d \mathbf{Q}_{md} Q m d
对每个c c c 0 ≤ c ≤ m 0 \leq c \leq m 0 ≤ c ≤ m d d d D 0 d \mathbf{D}_{0d} D 0 d D 1 d \mathbf{D}_{1d} D 1 d D m d \mathbf{D}_{md} D m d Q \mathbf{Q} Q d d d Q 0 d \mathbf{Q}_{0d} Q 0 d Q 1 d \mathbf{Q}_{1d} Q 1 d Q m d \mathbf{Q}_{md} Q m d s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m D 0 d \mathbf{D}_{0d} D 0 d D 1 d \mathbf{D}_{1d} D 1 d D m d \mathbf{D}_{md} D m d p p p s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m
给定次数p p p s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m d d d D 0 d \mathbf{D}_{0d} D 0 d D 1 d \mathbf{D}_{1d} D 1 d D m d \mathbf{D}_{md} D m d d d d Q 0 d \mathbf{Q}_{0d} Q 0 d Q 1 d \mathbf{Q}_{1d} Q 1 d Q m d \mathbf{Q}_{md} Q m d
因此,这其实就是一个曲线插值问题!全局曲线插值方法可以应用到数据点的每一列,从而求得每一列控制点Q c d \mathbf{Q}_{cd} Q c d n + 1 n+1 n + 1 n + 1 n+1 n + 1 Q \mathbf{Q} Q
现在,我们使用相同的思路,应用到Q i d \mathbf{Q}_{id} Q i d
Q i d = ∑ j = 0 n N j , q ( t d ) P i j \mathbf{Q}_{id}=\sum_{j=0}^{n}N_{j,q}(t_{d})\mathbf{P}_{ij}
Q i d = j = 0 ∑ n N j , q ( t d ) P i j
在这个等式中,Q \mathbf{Q} Q i i i Q i 0 \mathbf{Q}_{i0} Q i 0 Q i 1 \mathbf{Q}_{i1} Q i 1 Q i n \mathbf{Q}_{in} Q i n n + 1 n+1 n + 1 P i 0 \mathbf{P}_{i0} P i 0 P i 1 \mathbf{P}_{i1} P i 1 P i n \mathbf{P}_{in} P i n q q q t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n q q q t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n Q \mathbf{Q} Q i i i i i i
一旦找到所有行的控制点,这些控制点连同两个节点向量和次数p p p q q q m + 1 m+1 m + 1 n + 1 n+1 n + 1
Input: ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) D i j \mathbf{D}_{ij} D i j p , q p, q p , q Output: 一个经过所有数据点的次数为 (p , q p, q p , q
计算u u u s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m U U U v v v t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n V V V for d d d 0 0 0 to n n n do // 第d d d begin // 计算第d d d Q d \mathbf{Q}_d Q d p p p s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m U \mathbf{U} U D \mathbf{D} D d d d D 0 d , D 1 d , . . . , D m d \mathbf{D}_{0d}, \mathbf{D}_{1d}, ..., \mathbf{D}_{md} D 0 d , D 1 d , . . . , D m d d d d Q 0 d , Q 1 d , . . . , Q m d \mathbf{Q}_{0d}, \mathbf{Q}_{1d}, ..., \mathbf{Q}_{md} Q 0 d , Q 1 d , . . . , Q m d end
for c c c 0 0 0 to m m m do // 第c c c begin // 计算第c c c P c \mathbf{P}_c P c q q q t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n V \mathbf{V} V Q \mathbf{Q} Q c c c Q c 0 , Q c 1 , . . . , Q c n \mathbf{Q}_{c0}, \mathbf{Q}_{c1}, ..., \mathbf{Q}_{cn} Q c 0 , Q c 1 , . . . , Q c n c c c P c 0 , P c 1 , . . . , P c n \mathbf{P}_{c0}, \mathbf{P}_{c1}, ..., \mathbf{P}_{cn} P c 0 , P c 1 , . . . , P c n end
得到 ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) P i j \mathbf{P}_{ij} P i j ( p , q ) (p, q) ( p , q ) U \mathbf{U} U V \mathbf{V} V
第一个 for 循环中使用的矩阵 N \mathbf{N} N D = N Q \mathbf{D}=\mathbf{N}\mathbf{Q} D = N Q n + 1 n+1 n + 1 for 循环开始之前,应该先计算 N \mathbf{N} N LU分解 ,这样每次迭代中的插值都是简单的前向代换和后向代换。类似地,第二个 for 循环中的矩阵 N \mathbf{N} N LU分解 也应该在第二个 for 开始之前计算。如果不这样做,我们将执行 ( m + 1 + n + 1 = m + n + 2 ) (m+1 + n+1 = m + n + 2) ( m + 1 + n + 1 = m + n + 2 ) LU分解 ,而只需要2次就足够了。
因为插值曲面是通过 m + n + 2 m + n + 2 m + n + 2 。( m = 5 , n = 4 ) (m=5,n=4) ( m = 5 , n = 4 )
显然,改变数据点的位置会影响到整个曲面,这是一种全局的方法。
我们希望找到一个B样条曲面来逼近( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) u u u v v v p p p q q q e + 1 e+1 e + 1 f + 1 f+1 f + 1 m > e ≥ p ≥ 1 m > e \geq p \geq 1 m > e ≥ p ≥ 1 n > f ≥ q ≥ 1 n > f \geq q \geq 1 n > f ≥ q ≥ 1
全局曲面逼近:给定( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) D i j ( 0 ≤ i ≤ m , 0 ≤ j ≤ n ) \mathbf{D}_{ij} (0 \leq i \leq m ,0 \leq j \leq n) D i j ( 0 ≤ i ≤ m , 0 ≤ j ≤ n ) ( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) P i j ( 0 ≤ i ≤ e , 0 ≤ j ≤ f ) \mathbf{P}_{ij} (0 \leq i \leq e , 0 \leq j \leq f) P i j ( 0 ≤ i ≤ e , 0 ≤ j ≤ f ) ( p , q ) (p,q) ( p , q )
设由( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) P i j \mathbf{P}_{ij} P i j ( p , q ) (p,q) ( p , q )
S ( u , v ) = ∑ i = 0 e ∑ j = 0 f N i , p ( u ) N j , q ( v ) P i j S(u,v) = \sum_{i=0}^{e} \sum_{j=0}^{f} N_{i,p}(u)N_{j,q}(v)P_{ij}
S ( u , v ) = i = 0 ∑ e j = 0 ∑ f N i , p ( u ) N j , q ( v ) P i j
由于有m + 1 m+1 m + 1 n + 1 n+1 n + 1 m + 1 m+1 m + 1 u u u s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m n + 1 n+1 n + 1 v v v t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n 曲面的参数和节点向量 的讨论中给出了计算方法。
有了这些参数,曲面上与数据点 D c d \mathbf{D}_{cd} D c d
S ( s c , t d ) = ∑ i = 0 e ∑ j = 0 f N i , p ( s c ) N j , q ( t d ) P i j S(s_c, t_d) = \sum_{i=0}^{e} \sum_{j=0}^{f} N_{i,p}(s_c)N_{j,q}(t_d)\mathbf{P}_{ij}
S ( s c , t d ) = i = 0 ∑ e j = 0 ∑ f N i , p ( s c ) N j , q ( t d ) P i j
D c d \mathbf{D}_{cd} D c d
∣ D c d − S ( s c , t d ) ∣ 2 \left|\mathrm{D}_{cd}-\mathrm{S}(s_{c},t_{d})\right|^{2}
∣ D c d − S ( s c , t d ) ∣ 2
因此,所有误差距离平方的总和为:
f ( P 00 , P 01 , . . . , P e f ) = ∑ c = 0 m ∑ d = 0 n ∣ D c d − S ( s c , t d ) ∣ 2 f(P_{00}, P_{01}, ..., P_{ef}) = \sum_{c=0}^{m} \sum_{d=0}^{n} |\mathbf{D}_{cd} - S(s_c, t_d)|^2
f ( P 0 0 , P 0 1 , . . . , P e f ) = c = 0 ∑ m d = 0 ∑ n ∣ D c d − S ( s c , t d ) ∣ 2
这是关于( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) P i j \mathbf{P}_{ij} P i j f ( ) f() f ( ) f ( ) f() f ( )
∂ f ∂ P i j = 0 \frac{\partial f}{\partial\mathbf{P}_{ij}}=0
∂ P i j ∂ f = 0
然后,我们可以得到( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) 然而这些方程不是线性的,解决非线性方程组非常耗时,与其追求最优解,不如寻找一个合理的、但不是函数 f() 最小值的解。
为了找到一个非最优解,我们采用与全局曲面插值 中类似的方法。对每个数据点列应用曲线逼近以计算一些中间数据点 。
这样,每列 m + 1 m+1 m + 1 e + 1 e+1 e + 1 n + 1 n+1 n + 1 ( e + 1 ) × ( n + 1 ) (e+1) \times (n+1) ( e + 1 ) × ( n + 1 ) n + 1 n+1 n + 1 e + 1 e+1 e + 1 f + 1 f+1 f + 1 ( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 )
Input: ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) ( m + 1 ) × ( n + 1 ) D i j \mathbf{D}_{ij} D i j ( p , q ) (p,q) ( p , q ) ( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) Output: 逼近的( p , q ) (p, q) ( p , q )
计算u u u s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m U \mathbf{U} U v v v t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n V \mathbf{V} V for d d d 0 0 0 to n n n do // D \mathbf{D} D d d d begin // 计算"中间数据点"Q \mathbf{Q} Q p p p s 0 , s 1 , . . . , s m s_0, s_1, ..., s_m s 0 , s 1 , . . . , s m U \mathbf{U} U d d d D 0 d \mathbf{D}_{0d} D 0 d D 1 d \mathbf{D}_{1d} D 1 d D m d \mathbf{D}_{md} D m d d d d Q 0 d , Q 1 d , . . . , Q e d \mathbf{Q}_{0d}, \mathbf{Q}_{1d}, ..., \mathbf{Q}_{ed} Q 0 d , Q 1 d , . . . , Q e d Q \mathbf{Q} Q ( e + 1 ) × ( n + 1 ) (e+1) \times (n+1) ( e + 1 ) × ( n + 1 ) end
for c c c 0 0 0 to e e e do // Q \mathbf{Q} Q c c c begin // 计算所需的控制点P \mathbf{P} P q q q t 0 , t 1 , . . . , t n t_0, t_1, ..., t_n t 0 , t 1 , . . . , t n V \mathbf{V} V Q \mathbf{Q} Q c c c Q c 0 \mathbf{Q}_{c0} Q c 0 Q c 1 \mathbf{Q}_{c1} Q c 1 Q c n \mathbf{Q}_{cn} Q c n c c c P c 0 , P c 1 , . . . , P c f \mathbf{P}_{c0},\mathbf{P}_{c1}, ..., \mathbf{P}_{cf} P c 0 , P c 1 , . . . , P c f P \mathbf{P} P ( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) end
计算得到( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) P i j \mathbf{P}_{ij} P i j ( p , q ) (p, q) ( p , q ) U \mathbf{U} U V \mathbf{V} V
在这个算法中,先对D \mathbf{D} D n + 1 n+1 n + 1 e + 1 e+1 e + 1 n + e + 2 n + e + 2 n + e + 2 m + 1 m+1 m + 1 ( m + 1 ) × ( f + 1 ) (m+1) \times (f+1) ( m + 1 ) × ( f + 1 ) f + 1 f+1 f + 1 ( e + 1 ) × ( f + 1 ) (e+1) \times (f+1) ( e + 1 ) × ( f + 1 ) m + f + 2 m + f + 2 m + f + 2
由于这种算法并没有使得误差度量函数 f ( ) f() f ( )
注意,上面的算法中,第一个for 循环中使用的矩阵 N T ⋅ N \mathbf{N}^T·\mathbf{N} N T ⋅ N Q = ( N T ⋅ N ) P \mathbf{Q} =(\mathbf{N}^T·\mathbf{N})\mathbf{P} Q = ( N T ⋅ N ) P n + 1 n+1 n + 1 for 循环开始之前,应该对N T ⋅ N \mathbf{N}^T·\mathbf{N} N T ⋅ N L U \mathbf{L}\mathbf{U} L U for 循环会使用一个新的矩阵N T ⋅ N \mathbf{N}^T·\mathbf{N} N T ⋅ N for 开始之前对它进行L U \mathbf{L}\mathbf{U} L U ( e + 1 + ( n + 1 ) ) = e + n + 2 (e+1 + (n+1)) = e + n + 2 ( e + 1 + ( n + 1 ) ) = e + n + 2 L U \mathbf{L}\mathbf{U} L U
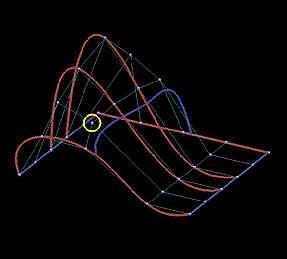
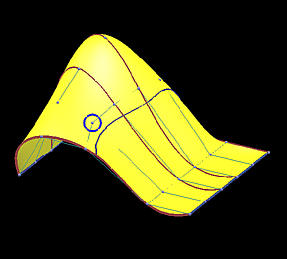
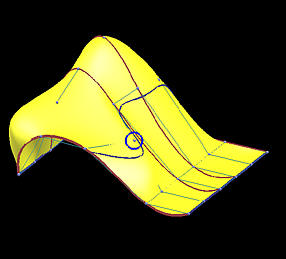
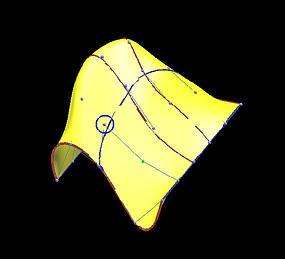
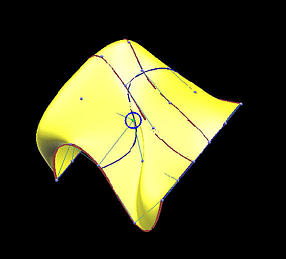
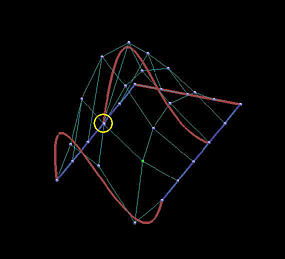
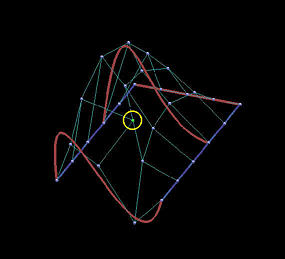
下面是一个6行5列数据点定义的网格。我们用它来说明插值方法和逼近方法之间的区别 。第一列的图像是移动黄色数据点之前的结果,第二列是移动了黄色数据点之后的结果。
第一行和第二行显示了使用弦长参数化确定参数的全局插值结果。插值曲面的次数为(3,3)。红色和蓝色曲线是节点处的等参数曲线。
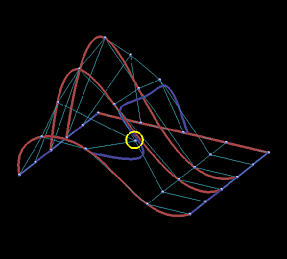
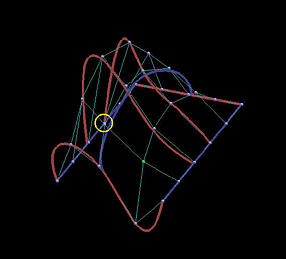
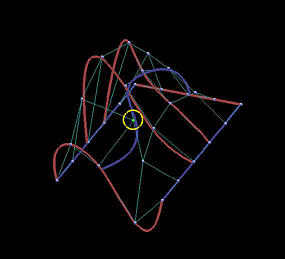
最后两行显示了全局逼近的结果。u u u v v v
结果表明,逼近曲面对数据点位置的改变不那么敏感,并且逼近曲面比插值曲面更好地贴近数据点网格的形状。
移动前
移动后
插值曲线
插值曲面
逼近曲线
逼近曲面




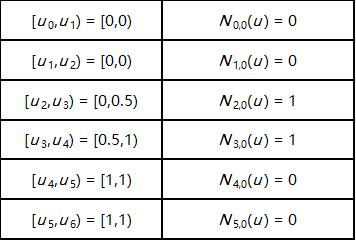
 (均匀法)
(均匀法) (弦长法)
(弦长法) (向心法)
(向心法) (通用方法)
(通用方法)