齐次坐标

使用齐次坐标的目的之一是表示无穷点。

在欧几里得坐标系中，无穷点是不存在的。但是如果使用无穷的概念，许多几何概念和计算可以大大简化。当我们进行曲线和表面设计时，这一点更加明显。

假设有两个实数，$a$ 和 $w$，计算 $\frac{a}{w}$ 的值。

我们保持 $a$ 的值不变，改变 $w$ 的值。随着 $w$ 变得越来越小，$\frac{a}{w}$ 的值变得越来越大。如果 $w$ 接近零，$\frac{a}{w}$ 就会接近无穷大！

因此，为了表示无穷大的概念，我们使用两个数 $a$ 和 $w$ 来表示一个值 $v$，$v=\frac{a}{w}$。如果 $w$ 不为零，那么该值就是 $\frac{a}{w}$。否则，我们用 $(a,0)$ 来表示无穷大的值。因此，无穷大的概念可以用 $(a, w)$ 或者 $\frac{a}{w}$ 来表示。

让我们把这个方法应用到$xy$坐标系上。如果我们使用$\frac{x}{w}$和$\frac{y}{w}$替换$x$和$y$，那么函数$f(x,y)=0$就变成了$f(\frac{x}{w},\frac{y}{w})=0$，将它与系数$w^n$的数相乘就可以消除掉所有分母，其中$n$是多项式的次数。

例如，假设我们有一条线 $Ax + By + C = 0$。将 $x$ 和 $y$ 替换为 $\frac{x}{w}$ 和 $\frac{y}{w}$ 得到 $A(\frac{x}{w}) + B(\frac{y}{w}) + C$ = 0。乘以 $w$ 会变为

$$Ax + By + Cw = 0$$

给定方程为二次多项式 $Ax^2 + 2Bxy + Cy^2 + 2Dx + 2Ey + F$ = 0。在将 $x$ 和 $y$ 替换为 $\frac{x}{w}$ 和 $\frac{y}{w}$ 并乘以 $w^2$ 后，我们得到

$$Ax^2+2Bxy+Cy^2+2Dxw+2Eyw+Fw^2=0$$

如果你仔细观察这两个多项式，你会发现所有项的次数是相等的。在直线的情况下，项$x$、$y$ 和 $w$ 的次数都是一次，而在二次多项式中，所有项(即$x^2$，$xy$，$y^2$，$xw$，$yw$ 和 $w^2$)的次数都是二次。

给定一个$n$次多项式，在引入$w$后，所有的项都是$n$次的。因此，这些多项式被称为齐次多项式，而坐标$(x,y,w)$则被称为齐次坐标。

给定一个在齐次坐标系统中的$n$次多项式，将该多项式除以$w^n$，然后将$\frac{x}{w}$和$\frac{y}{w}$分别替换为$x$和$y$，将会将该多项式转换回常规形式。例如，如果给定的3次齐次多项式如下所示：

$$x^3 + 3xy^2 - 5y^2w + 10w^3 = 0$$

经过转换后，结果是

$$x^3 + 3xy^2 - 5y^2 + 10 = 0$$

这个规则也适用于三维。可以将点$(x, y, z)$替换为$(\frac{x}{w}, \frac{y}{w},\frac{z}{w})$，并将结果乘以$w$的某个幂。所得的多项式是齐次的。

一个重要的说明

给定一个齐次坐标系中的点$(x,y,w)$，它在$xy$平面上对应的点是什么？根据前面的讨论，很容易得到，是$(\frac{x}{w},\frac{y}{w})$。
因此，一个在齐次坐标系中的点$(3,4,5)$ 转换为$xy$平面上的点为$(3/5,4/5)=(0.6,0.8)$。
同样，一个在齐次坐标系中的点$(x,y,z,w)$转换为空间中的点为$(x/w,y/w,z/w)$。
相反，$xy$ 平面上一点 $(x,y)$的齐次坐标是什么？简单地说就是 $(x,y,1)$ 。即 $w$ 分量为 1。
$xy$ 平面上一点 $(x,y)$ 的齐次坐标是 $(xw, yw, w)$，其中 $w$ 是任意非零数。

我们有结论：
将齐次坐标转换为常规坐标是唯一的；但是，将常规坐标转换为齐次坐标则不是。

例如，空间中的点 $(4,2,3)$ 转换成齐次坐标为 $(4w, 2w, 3w, w)$, 其中$w$为非零值，可以有无数种可能。

无穷远点

设一个点坐标为$(x,y)$，通过乘以$\frac{1}{w}$转换为齐次坐标，即$(\frac{x}{w},\frac{y}{w},\frac{1}{w})$。

当$w$的值接近于零时，点$(\frac{x}{w},\frac{y}{w})$就会朝着$(x,y)$的方向越来越远。当$w$变为零时，点$(\frac{x}{w},\frac{y}{w})$就移动到了无穷远处。

因此，我们可以说，齐次坐标$(x,y,0)$是指向$(x,y)$方向的无穷远点。

(3,5)是$xy$平面上的一个点。考虑点$(\frac{3}{w},\frac{5}{w})$，该点是直线 $O + \frac{d}{w}$上的一个点，其中$O$是坐标原点，$d$是方向向量$<3,5>$。因此，当$w$趋近于零时，该点在直线上无限远处。

对于空间中的点也是一样的，$(x, y, z, 0)$是指向$(x, y, z)$方向的无穷远点。

齐次坐标的几何解释

假设在$xy$平面上给定一个点的齐次坐标为$(x,y,w)$，$(x,y,w)$视为空间中的一个点，其坐标值分别为$x$、$y$和$w$，对应于$x$轴、$y$轴和$w$轴。连接这一点和坐标原点的直线与平面$w$ = 1相交于点$(\frac{x}{w}, \frac{y}{w}, 1)$。如下图所示

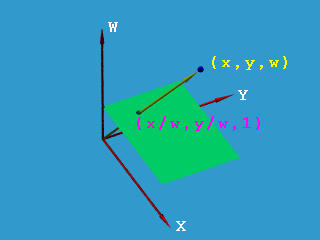
这个转换将二维齐次坐标点视为三维空间中的点，并将这个三维点（从坐标原点）投影到平面$w=1$上。因此，当一个由齐次多项式$f(x,y,w)=0$定义的齐次点沿着曲线移动时，它对应的点在三维空间中移动，当这个点被投影到平面$w=1$上。这个点$(\frac{x}{w},\frac{y}{w})$在平面$w=1$上也沿着类似的曲线移动。

以上图形清楚地显示，从传统的欧几里德坐标转换为齐次坐标是唯一的，但反向转换不是，因为沿着原点和$(x,y,w)$连线上的所有点都可以映射成齐次坐标点$(\frac{x}{w}, \frac{y}{w}, 1)$。