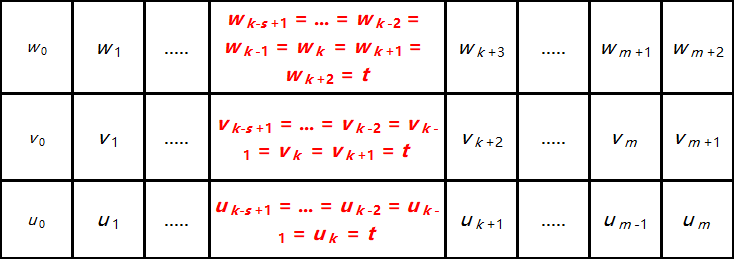B 样条曲线

B样条曲线的由来

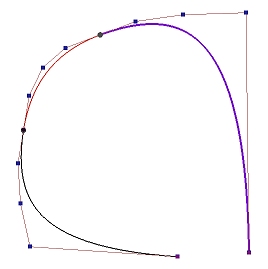
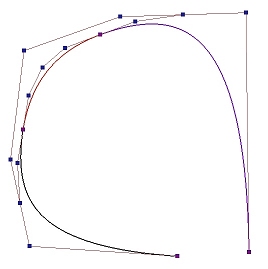
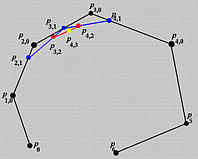
假设我们要设计一个花瓶的剖面，下图是一个$11$阶的$Bézier$曲线，如果想要让花瓶的"颈部"向着线段$P_4-P_5$的位置弯曲是比较困难的。

一种解决方法是，我们可以在这段颈部附近添加更多控制点以增加该区域的权重。但是，这将增加曲线的阶数。在许多情况下，使用这样高阶多项式是不值得的。

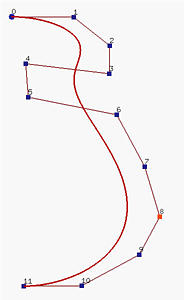
另一种方式是，我们可以将两个 $Bézier$ 曲线连接在一起。 只要第一条曲线的最后一段和第二条曲线的第一段方向相同，我们可以保证 $G^1$ 连续性，即切点处朝两边的切向量具有相同的方向但可能长度不同（如果长度相同，则为 $C^1$ 连续）。 下图展示了这种方式， 它由三个三阶$Bézier$曲线连接而成，连接点用黄色矩形标记。 这说明，通过连接多个低阶 $Bézier$曲线段，并满足$G^1$连续，我们仍然可以设计复杂的形状。 但是，要保持这种$G^1$连续条件可能很繁琐且不理想。

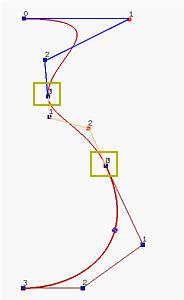
有没有可能我们仍然使用低阶曲线段而无需担心$G^1$连续条件？

B样条曲线是 Bézier 曲线的泛化，即更通用的版本，可以解决上面这个问题。

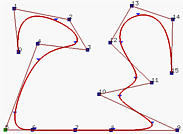
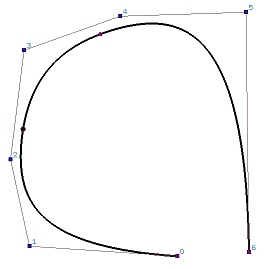
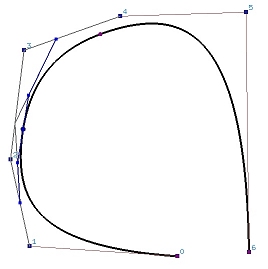
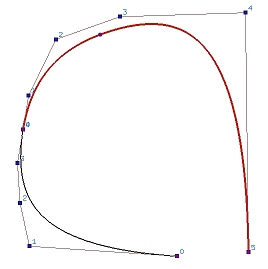
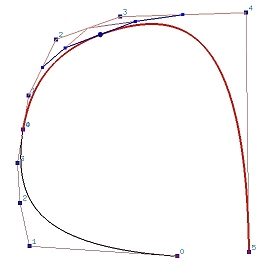
下图是由 $8$个控制点定义的三次B样条曲线。 实际上，也可以看作是由5个三次的 Bézier 曲线段连接在一起（曲线上每两个点之间的曲线段就可以看是一段Bézier 曲线），形成由控制点定义的B样条曲线。 可以移动控制点以修改曲线的形状， 我们还可以在曲线上增加新的点，分成更多的Bézier 曲线段。 因此，B样条曲线在曲线设计中具有更高的自由度。

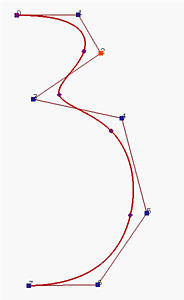
如果曲线的定义域是$[0,1]$，位于曲线上的点，我们称为节点，节点将曲线分成不同的曲线段，这些节点满足 $0\leq u_0\leq u_1\leq... \leq u_m\leq1$。 $C(u_i)$ 表示曲线上的一点，因此改变节点的值，即修改$u_i$的位置，会改变曲线的形状。

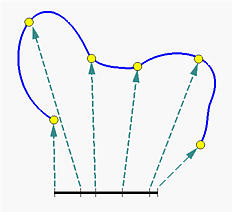
总之，要设计一个B样条曲线，我们需要一组控制点（像贝塞尔曲线一样需要具有控制点）、一组节点（用来将B样条分成多个贝塞尔曲线段）以及一组系数（用来保证每个贝塞尔曲线段连接处具有一定的连续性），每个控制点对应一个系数，以便所有的曲线段连接在一起满足某种连续性条件。

B样条基函数的定义

还记得贝塞尔曲线的公式吗？

$$\mathbf{C}(u)=\sum_{i=0}^nB_{n,i}(u)\mathbf{P}_i$$

其中每个控制点都有一个权重函数$B_{n,i}(u)$，B样条曲线中也采用类似的基函数；但B样条曲线中的基函数要复杂得多。

它具有两个特殊的性质：
（1）基函数的定义域并非整个曲线（$[0,1]$），而是通过节点被划分成一个小的区域，如$[u_{i},u_{i+1}]$。
（2）基函数并非在整个定义域上都是非零的。而是在其所在的区间上非零，因此，B样条基函数具有很强的"局部性"。

后面会详细介绍这两条性质

设$U$是一组$m+1$个非递减数，$u_0 \leq u_2 \leq u_3 \leq ... \leq u_m$。这些$u_i$被称为节点，集合$U$被称为节点向量，半开区间$[u_i, u_{i+1})$是第$i$个节点区间。

需要注意的是，由于一些$u_i$可能相等，某些节点区间可能不存在（即区间长度为0）。

• 如果一个节点$u_i$出现$k$次（即，$u_i = u_{i+1} = ... = u_{i+k-1}$，其中$k > 1$），那么$u_i$就是一个重复度（multiplicity）为$k$的多重节点，记作$u_i(k)$。
• 如果$u_i$只出现一次，它就是一个简单节点。
• 如果节点等间隔分布（即，对于$0 \leq i \leq m - 1$，$u_{i+1} - u_i$是一个常数），则该节点向量或节点序列被称为均匀的；否则，它是非均匀的。

节点可以被看作是将区间$[u_0, u_m]$细分为更小节点区间的分割点。所有B样条基函数的定义域都被假定为$[u_0, u_m]$。通常我们使用$u_0 = 0$和$u_m = 1$，使得定义域是闭区间$[0,1]$。

要定义B样条基函数，我们还需要知道基函数的次数$p$。第$i$个次数为$p$的B样条基函数，记作$N_{i,p}(u)$，其定义如下：

$$N_{i,0}(u)=\left\{\begin{array}{lll}1&\quad\text{if}u_i\le u<u_{i+1}\\\\0&\quad\text{otherwise}\end{array}\right.$$

$$N_{i,p}(u)=\frac{u-u_{i}}{u_{i+p}-u_{i}}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)$$

上述通常被称为$Cox-deBoor$递归公式。这个定义看起来复杂；但实际上并不难理解。如果次数为零（即$p = 0$），这些基函数都是阶梯函数，这也是上面第一个公式表达的内容。即，如果$u$位于第$i$个节点区间$[u_i, u_{i+1})$内，则基函数$N_{i,0}(u)$为1。

例如，如果我们有四个节点$u_0 = 0, u_1 = 1, u_2 = 2$和$u_3 = 3$，节点区间分别是$[0,1)、[1,2)、[2,3)$，次数为0的基函数$N_{0,0}(u)$在$[0,1)$区间上为1，在其他区间上为0，$N_{1,0}(u)$在$[1,2)$区间上为1，在其他区间为0，$N_{2,0}(u)$在$[2,3)$区间上为1，在其他区间为0。如下图所示：

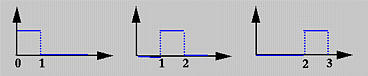
为了理解当$p > 0$时计算$N_{i,p}(u)$的方式，我们使用了三角形计算方案。所有节点区间列在左侧（第一）列，所有零次基函数在第二列。如下图：

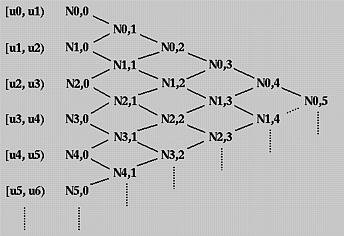
要计算$N_{i,1}(u)$，则需要知道$N_{i,0}(u)$和$N_{i+1,0}(u)$。

因此，我们可以先计算$N_{0,1}(u)$、$N_{1,1}(u)$、$N_{2,1}(u)$、$N_{3,1}(u)$等等。所有这些$N_{i,1}(u)$都写在第三列。一旦所有$N_{i,1}(u)$都计算完毕，我们就可以计算$N_{i,2}(u)$，并将它们放在第四列。如此计算，直到所有需要的$N_{i,p}(u)$都被计算出来。

在上述过程中，我们已经得到了节点向量$U = \{0, 1, 2, 3\}$对应的$N_{0,0}(u)$、$N_{1,0}(u)$和$N_{2,0}(u)$值。现在让我们计算$N_{0,1}(u)$和$N_{1,1}(u)$。

计算$N_{0,1}(u)$，已知$i = 0$且$p = 1$，根据定义我们有：

$$N_{0,1}(u)=\frac{u-u_0}{u_1-u_0}N_{0,0}(u)+\frac{u_2-u}{u_2-u_1}N_{1,0}(u)$$

由于 $u_0 = 0$，$u_1 = 1$ 和 $u_2 = 2$，则上式变成：

$$N_{0,1}(u)=uN_{0,0}(u)+(2-u)N_{1,0}(u)$$

由于$N_{0,0}(u)$在$[0,1)$区间非零，且$N_{1,0}(u)$在$[1,2)$区间非零。如果$u$在$[0,1)$区间内，只有$N_{0,0}(u)$对$N_{0,1}(u)$有贡献。因此：

如果$u$在$[0,1)$区间内，$N_{0,1}(u) = uN_{0,0}(u) = u$；
如果$u$在$[1,2)$区间内，$N_{0,1}(u) = (2 - u)N_{1,0}(u) = (2 - u)$。

类似的计算可以得出，如果$u$在$[1,2)$区间内，$N_{1,1}(u) = u - 1$；如果$u$在$[2,3)$区间内，$N_{1,1}(u) = 3 - u$。在下图中，黑线和红线分别代表$N_{0,1}(u)$和$N_{1,1}(u)$。注意，$N_{0,1}(u)$在$[0,1)$和$[1,2)$区间内非零，$N_{1,1}(u)$在$[1,2)$和$[2,3)$区间内非零

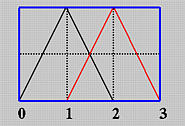
有了$N_{0,1}(u)$和$N_{1,1}(u)$的值，我们就可以计算$N_{0,2}(u)$。根据定义，我们有：

$$N_{0,2}(u)=\frac{u-u_0}{u_2-u_0}N_{0,1}(u)+\frac{u_3-u}{u_3-u_1}N_{1,1}(u)$$

将节点的值代入

$$N_{0,2}(u)=0.5uN_{0,1}(u)+0.5(3-u)N_{1,1}(u)$$

其中，$N_{0,1}(u)$在$[0,1)$和$[1,2)$区间非零，$N_{1,1}(u)$在$[1,2)$和$[2,3)$区间非零。因此，我们需要考虑三种情况：

• **$u$在$[0,1)$区间内：**在这种情况下，只有$N_{0,1}(u)$对$N_{0,2}(u)$的值有贡献。由于$N_{0,1}(u)$等于$u$，因此，在$[0,1)$区间上，我们有$N_{0,2}(u)=0.5u^{2}$
• **$u$在$[1,2)$区间内：**在这种情况下，$N_{0,1}(u)$和$N_{1,1}(u)$都对$N_{0,2}(u)$有贡献。由于$N_{0,1}(u) = 2 - u$且$N_{1,1}(u) = u - 1$，因此，在$[1,2)$区间上，我们有

  $$N_{0,2}(u)=(0.5u)(2-u)+0.5(3-u)(3-u)=0.5(-3+6u-2u^2)$$

• $u$在$[2,3)$区间内：在这种情况下，只有$N_{1,1}(u)$对$N_{0,2}(u)$有贡献。由于$N_{1,1}(u) = 3 - u$，因此，在$[2,3)$区间上，我们有

  $$N_{0,2}(u)=0.5(3-u)(3-u)=0.5(3-u)^{2}$$

如果我们绘制上述每种情况的曲线段，我们将看到两个相邻的曲线段在节点处连接起来，形成一条曲线。更准确地说，第一种和第二种情况的曲线段在$u = 1$处连接，而第二种和第三种情况的曲线段在$u = 2$处连接。注意，这里合成的曲线是平滑的。但是，通常情况下，如果节点向量中包含多重节点，就并非如此。

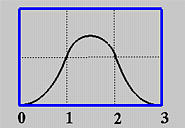
两个重要的观察

由于$N_{i,1}(u)$是基于$N_{i,0}(u)$和$N_{i+1,0}(u)$计算得来的，而$N_{i,0}(u)$和$N_{i+1,0}(u)$分别在区间$[u_i, u_{i+1})$和$[u_{i+1}, u_{i+2})$上非零，因此$N_{i,1}(u)$在这两个区间上非零。换句话说，$N_{i,1}(u)$在区间$[u_i, u_{i+2})$上非零。

同理，由于$N_{i,2}(u)$依赖于$N_{i,1}(u)$和$N_{i+1,1}(u)$，而这两个基函数分别在$[u_i, u_{i+2})$和$[u_{i+1}, u_{i+3})$上非零，$N_{i,2}(u)$在$[u_i, u_{i+3})$上非零。

一般来说，要确定一个基函数$N_{i,p}(u)$的非零定义域，可以通过使用三角计算方案向回追溯直到达到第一列。被覆盖的区间就是这个基函数的非零定义域。

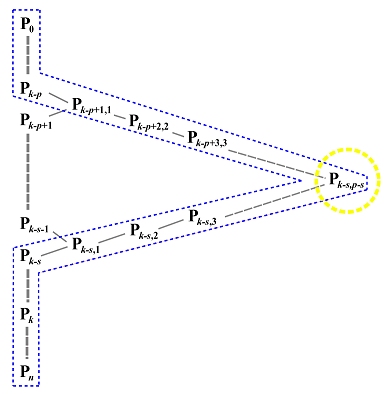
例如，假设我们想找出$N_{1,3}(u)$的非零定义域，我们可以沿着西北和西南方向追溯，直到达到第一列，如下图中的蓝色虚线所示。因此，$N_{1,3}(u)$在$[u_1, u_2)$、$[u_2, u_3)$、$[u_3, u_4)$和$[u_4, u_5)$上非零。或者说它在$[u_1, u_5)$上非零。

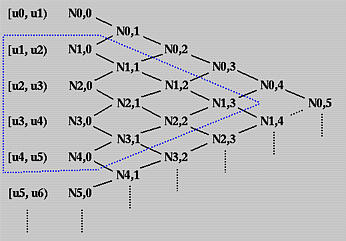
因此我们有以下结论：

基函数$N_{i,p}(u)$在$[u_i, u_{i+p+1})$区间非零。或者说，$N_{i,p}(u)$在连续的$p+1$个节点区间$[u_i, u_{i+1})$、$[u_{i+1}, u_{i+2})$、…、$[u_{i+p}, u_{i+p+1})$上非零。

接着，我们看相反的方向。给定一个节点区间$[u_i, u_{i+1})$，我们想知道哪些基函数在其计算中会使用这个区间。我们可以从这个节点区间开始，向东北和东南方向各画一条箭头。所有在这个楔形范围内的基函数都会使用$N_{i,0}(u)$。因此，所有在$[u_i, u_{i+1})$上非零的$p$次基函数都是这个楔形与包含所有$N_{i,p}(u)$的那一列的交集。

实际上，这一列和两条箭头形成了一个等边三角形，这一列是垂直边。
从$N_{i,0}(u)$数到$N_{i,p}(u)$，总共有$p+1$列。因此，等边三角形的垂直边最多有$p+1$个条目，即$N_{i,p}(u)$、$N_{i-1,p}(u)$、$N_{i-2,p}(u)$、…、$N_{i-p+2,p}(u)$、$N_{i-p+1,p}(u)$和$N_{i-p,p}(u)$。如下图所示：

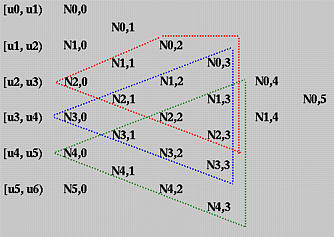
例如：要找到所有在$[u_4, u_5)$区间非零的3次基函数，画两条箭头，所有在垂直边上的函数就是我们要找的。在上图中，它们是$N_{1,3}(u)$、$N_{2,3}(u)$、$N_{3,3}(u)$和$N_{4,3}(u)$。这用橙色三角形表示。蓝色三角形显示了在$[u_3, u_4)$区间非零的3次基函数，红色三角形显示了在$[u_2, u_3)$区间非零的3次基函数。

因此我们有以下结论：

在任何节点区间$[u_i, u_{i+1})$上，最多有$p+1$个$p$度基函数是非零的，分别是：$N_{i-p,p}(u)$、$N_{i-p+1,p}(u)$、$N_{i-p+2,p}(u)$、…、$N_{i-1,p}(u)$和$N_{i,p}(u)$

基函数中系数的含义是什么？

最后，让我们探究基函数$N_{i,p}(u)$定义中系数的含义。在计算$N_{i,p}(u)$时，它使用了$N_{i,p-1}(u)$和$N_{i+1,p-1}(u)$，前者在$[u_i, u_{i+p})$区间非零。如果$u$在这个半开区间内，则$u - u_i$是$u$与该区间左端的距离，区间长度是$u_{i+p} - u_i$，而$\frac{u - u_i}{u_{i+p} - u_i}$是上述距离的比例，总是在0和1的范围内。如下图所示。

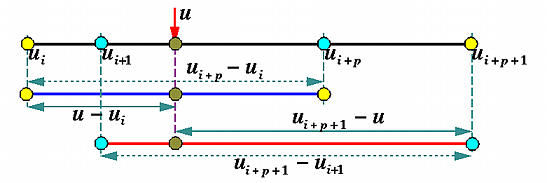
第二项$N_{i,p-1}(u)$，在$[u_{i+1}, u_{i+p+1})$区间非零。如果$u$在这个区间内，则$u_{i+p+1} - u$是$u$到该区间右端的距离，$u_{i+p+1} - u_{i+1}$是区间长度，$\frac{u_{i+p+1} - u}{u_{i+p+1} - u_{i+1}}$是这两个距离的比例，其值在0和1之间

因此，$N_{i,p}(u)$是$N_{i,p-1}(u)$和$N_{i+1,p-1}(u)$的线性组合，带有两个系数，这两个系数都是$u$的线性函数，其值都在0和1之间。

B样条基函数的性质

B样条曲线基函数的定义：

$$N_{i,0}(u)=\left\{\begin{array}{lll}1&\quad\text{if}u_i\le u<u_{i+1}\\\\0&\quad\text{otherwise}\end{array}\right.$$

$$N_{i,p}(u)=\frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)$$

这组基函数具有以下性质，其中许多性质与贝塞尔曲线的基函数相似

1. $N_{i,p}(u)$是关于$u$的$p$阶多项式
2. 非负性：
   对于所有$i$、$p$和$u$,$N_{i,p}(u)$是非负的
3. 局部性：
   $N_{i,p}(u)$在区间$[u_i,u_{i+p+1})$上是非零多项式，在其他区间上是0。
4. 在任何区间$[u_i,u_{i+1})$上，最多有$p+1$个$p$阶基函数不为零
   即:$N_{i-p,p}(u)、N_{i-p+1,p}(u)、N_{i-p+2,p}(u)、...、和 N_{i,p}(u)$
5. 单位分解 ：在区间$[u_i,u_{i+1})$上所有非零的$p$阶基函数之和为1
   上一条的性质表明，$N_{i-p,p}(u)、N_{i-p+1,p}(u)、N_{i-p+2,p}(u)、...、和N_{i,p}(u)$在$[u_i,u_{i+1})$上都不为零。这条性质表明这$p+1$个基函数之和为1。
6. 如果节点数为$m+1$，基函数的阶数为$p$，$p$阶基函数的数量为$n+1$，则满足条件$m=n+p+1$。
   设$N_{n,p}(u)$为最后一个$p$阶基函数，它在$[u_n,u_{n+p+1})$上不为零。由于它是最后一个基函数，$u_{n+p+1}$必须是最后一个节点$u_m$。因此,我们有$u_{n+p+1}=u_m$和$n+p+1=m$。总之，给定$m$和$p$,令$n=m-p-1$,则$p$阶基函数为$N_{0,p}(u)、N_{1,p}(u)、N_{2,p}(u)、...、和N_{n,p}(u)$。
7. 基函数$N_{i,p}(u)$是一条由$p$阶多项式组成的复合曲线，其连接点位于区间$[u_i,u_{i+p+1})$的节点处。
   例如,$N_{0,2}(u)$在$[0,3)$上不为零，由定义在$[0,1)、[1,2)$和$[2,3)$上的三条抛物线构成，它们在节点2和3处连接在一起。
8. 在重复度为$k$的节点处,基函数$N_{i,p}(u)$是$C^{p-k}$连续的。
   因此，重复度越高，连续性级别越低，而阶数越高，连续性越好。上面提到的二阶基函数$N_{0,2}(u)$在节点2和3处是$C^1$连续的，因为它们是简单节点($k=1$)。

多重节点的影响

多重节点对基函数的计算和一些"计算"性质有很重要的影响 。我们看两个例子：

（1）每个重复度为k的节点最多会减少k-1个基函数的非零定义域。

以$N_{i,p}(u)$和$N_{i+1,p}(u)$为例。前者在$[u_i,u_{i+p+1})$上不为零，而后者在$[u_{i+1},u_{i+p+2})$上不为零。如果我们将$u_{i+p+2}$移动到$u_{i+p+1}$，使它们成为一个双重节点。那么,$N_{i,p}(u)$仍然有$p+1$个节点区间不为零；但是,$N_{i+1,p}(u)$不为零的节点区间数量减少了一个，因为区间$[u_{i+p+1},u_{i+p+2})$消失了。

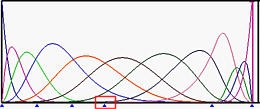
下图显示了5阶B样条基函数，其中左端和右端节点的重复度为6，而中间所有节点都是简单节点(图(a))。图(b)是将$u5$移动到$u6$的结果。那些在$u6$处结束的基函数对应的非零节点区间减少了。然后移动$u4$到$u6$，再将$u3$移动到$u6$，使$u6$成为一个重复度为4的节点(图©和(d))。图(e)显示了将$u2$移动到$u6$之后的结果，创建了一个重复度为5的节点。

(a):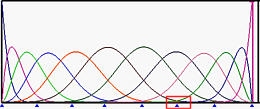

(b):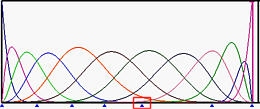

©:

(d):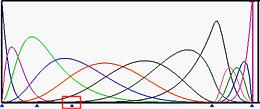

(e):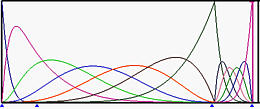

（2）在每个内部重复度为k的节点处,非零基函数的数量最多为p-k+1,其中p是基函数的阶数。

由于将$u_{i-1}$移动到$u_i$会将一个在$u_{i-1}$处结束的非零基函数拉到$u_i$处结束，因此会减少在$u_i$处非零基函数的数量。更确切地说，将$u_i$的重复度增加1会使非零基函数的数量减少1。由于在$u_i$处最多可以有$p+1$个非零基函数,所以在一个重复度为$k$的节点处,非零基函数的数量最多为$(p+1)-k=p-k+1$。

在上面的图中,由于节点$u_6$的重复度分别为$1、2、3、4$和$5$,所以在$u_6$处的非零基函数数量分别为$5、4、3、2$和$1$。

B样条基函数的计算示例

本章节介绍两个B样条基函数计算的例子，一个使用简单节点，另一个使用多重节点。

简单节点

假设节点向量为 $U = \{0, 0.25, 0.5, 0.75, 1\}$。可以到得到$m = 4$,$u_0 = 0$,$u_1 = 0.25$,$u_2 = 0.5$,$u_3 = 0.75$和$u_4 = 1$。

0次基函数的计算很容易，即是$N_{0,0}(u)$、$N_{1,0}(u)$、$N_{2,0}(u)$和$N_{3,0}(u)$，分别定义在节点范围$[0,0.25)$、$[0.25,0.5)$、$[0.5,0.75)$和$[0.75,1)$上，并在各自的定义区间上值为1，在其他区间上值为0，基函数如下所示：

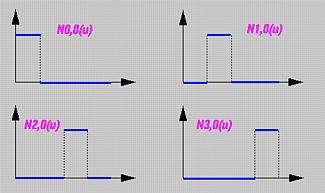
下表给出了所有的$N_{i,1}(u)$:

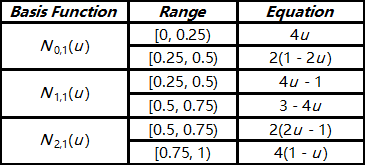
下图展示了这些基函数的图形：

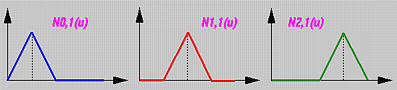
节点$0.25$, $0.5$和$0.75$都是简单的(即，$k = 1$) 且$p = 1$，有$p - k + 1 = 1$个非零基函数和三个节点。并且，$N_{0,1}(u)$, $N_{1,1}(u)$ 和 $N_{2,1}(u)$在节点$0.25$, $0.5$ 和 $0.75$分别是$C^0$ 连续的。

从$N_{i,1}(u)$可计算2次基函数。根据$m = 4$, $p = 2$, 和 $m = n + p + 1$，我们可以得到$n = 1$所以只有两个2次基函数：$N_{0,2}(u)$和 $N_{1,2}(u)$。结果见下表：

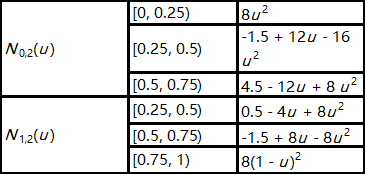
下图展示了这两个基函数：

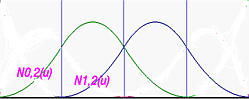
三条垂直的蓝线表示节点的位置。需要注意的是，每个基函数都是由三个二次曲线段组成的复合曲线。例如，$N_{0,2}(u)$ 是绿色曲线，它是在区间$[0,0.25)$，$[0.25, 0.5)$ 和 $[0.5,0.75)$ 上定义的三个抛物线的并集。这三个曲线段连接在一起形成一个平滑的钟形。在这些节点上，这个复合曲线具有 $C^1$ 连续性。

带有正重复度的节点

如果$u_i$是一个重复度为$k$的节点（即$u_i = u_{i+1} = \dots = u_{i+k-1}$），那么节点区间$[u_i,u_{i+1})，[u_{i+1},u_{i+2})，\dots，[u_{i+k-2},u_{i+k-1})$不存在，因此$N_{i,0}(u)$，$N_{i+1,0}(u)，\dots，N_{i+k-1,0}(u)$都是零函数。

考虑一个节点向量$U = \{ 0, 0, 0, 0.3, 0.5, 0.5, 0.6, 1, 1, 1 \}$。因此，0和1的重复度为3（即$0{(3)}$和$1{(3)}$），0.5的重复度为2（即$0.5{(2)}$）。$m = 9$，节点分配如下:

现在计算 $N_{i,0}(u)$。 注意因为 $m = 9$ 且 $p = 0$ ( 0 次基函数), 我们有$n = m - p - 1 = 8$。如下表所示，只有四个0次非零基函数： $N_{2,0}(u)$, $N_{3,0}(u)$, $N_{5,0}(u)$ 和 $N_{6,0}(u)$.

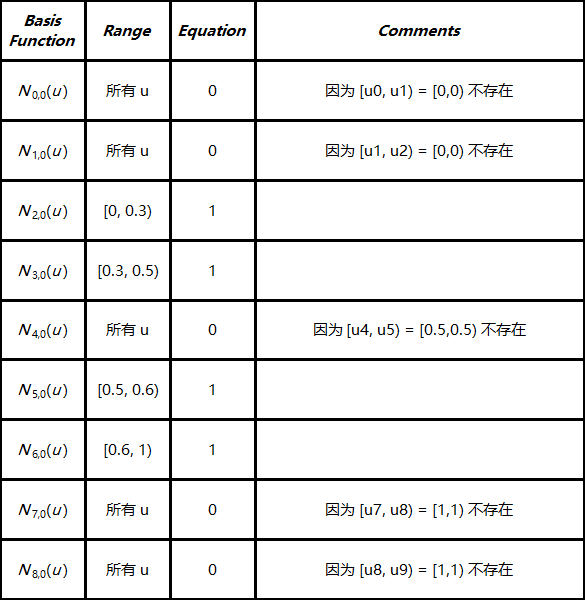
然后，我们继续计算1次基函数。因为 $p$ 为 1, $n = m - p - 1 = 7$。下表显示了结果：

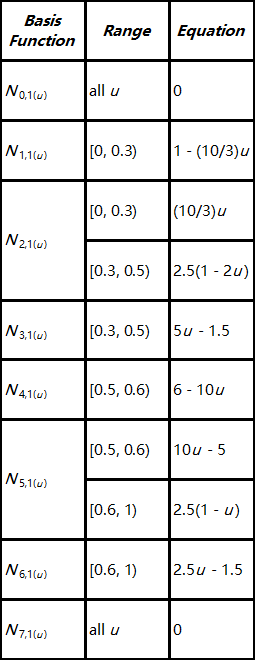
下图显示了这些基函数的图形：

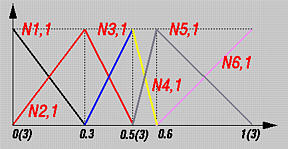
我们详细说明其中一项的具体计算过程，比如$N_{1,1}(u)$。它使用下式计算：

$$N_{1,1}(u)=\frac{u-u_1}{u_2-u_1}N_{1,0}(u)+\frac{u_3-u}{u_3-u_2}N_{2,0}(u)$$

将$u_1 = u_2 = 0$和$u_3 = 0.3$代入上式得到：

$$N_{1,1}(u) = \frac{u - 0}{0.3 - 0}N_{1,0}(u) + \frac{0.3 - u}{0.3 - 0}N_{2,0}(u)$$

由于$N_{1,0}(u)$在任何地方都是零，第一项变成了$0/0$，我们定义0/0为0。因此，只有第二项对结果产生影响，而$N_{2,0}(u)$在$[0,0.3)$上为1，所以，$N_{1,1}(u)$在$[0,0.3)$上为$(1 - \frac{10}{3}u)$。

接下来，让我们计算所有$N_{i,2}(u)$。由于$p = 2$，我们有$n = m - p - 1 = 6$。下面的表格包含了所有$N_{i,2}(u)$：

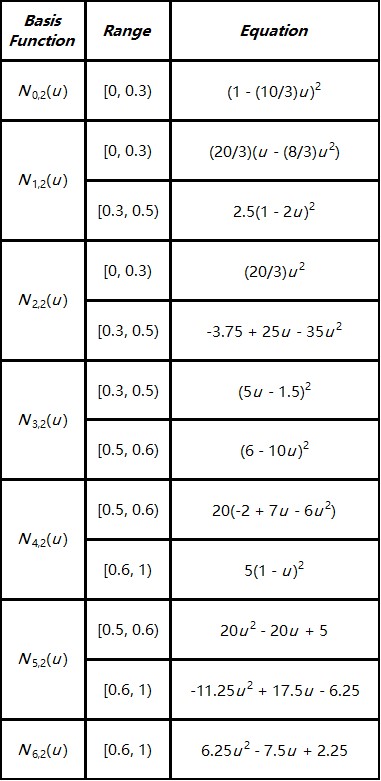
下图显示了所有2次基函数：

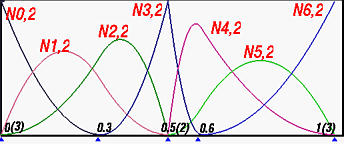
我们详细说明其中一项的具体计算过程，如$N_{3,2}(u)$。计算式为：

$$N_{3,2}(u) = \frac{u - 0.3}{0.5 - 0.3}N_{3,1}(u) + \frac{0.6 - u}{0.6 - 0.5}N_{4,1}(u)$$

代入$u_3 = 0.3$，$u_4 = u_5 = 0.5$和$u_6 = 0.6$得到

$$N_{3,2}(u) = \frac{u - 0.3}{0.2}N_{3,1}(u) + \frac{0.6 - u}{0.1}N_{4,1}(u)$$

由于$N_{3,1}(u)$在区间$[0.3, 0.5)$上不为零，且等于$(5u - 1.5)$，因此可以得到$N_{3,2}(u)$在区间$[0.3, 0.5)$上为$(5u - 1.5)^2$。

由于$N_{4,1}(u)$在区间$[0.5, 0.6)$上不为零，且等于$(6 - 10u)$，因此可以得到$N_{3,2}(u)$在区间[0.5, 0.6)上是$(6 - 10u)^2$。

在节点$0.5{(2)}$，由于其重复度为2，且这些基函数的次数为2，基函数$N_{3,2}(u)$在$0.5{(2)}$处是$C^0$连续的。这就是为什么$N_{3,2}(u)$在$0.5{(2)}$处有一个锐角。对于不在两端的节点，比如0.3，由于它们都是简单节点，因此保持了$C^1$连续性。

B样条曲线的定义

给定$n+1$个控制点$\mathbf{P}_0, \mathbf{P}_1, ..., \mathbf{P}_n$和一个节点向量$U = {u_0, u_1, ..., u_m}$，由这些控制点和节点向量$U$定义的$p$次B-样条曲线为:

$$\mathbf{C}(u) = \sum_{i=0}^{n}N_{i,p}(u)\mathbf{P}_i$$

其中$N_{i,p}(u)$是$p$次B样条基函数。B样条曲线的形式与贝塞尔曲线非常相似。与贝塞尔曲线不同的是，B样条曲线涉及更多信息：一组$n+1$个控制点、$m+1$个节点的节点向量和次数p，其中$n、m$和$p$必须满足$m = n + p + 1$。

如果我们想定义一条具有$n+1$个控制点的p次B-样条曲线，我们必须提供$n+p+2$个节点$u_0, u_1, ..., u_{n+p+1}$。或者说，如果给定$m+1$个节点的节点向量和$n+1$个控制点,则B样条曲线的次数为$p = m - n - 1$。

与节点$u_i$对应的曲线上的点$\mathbf{C}(u_i)$被称为节点点。因此,节点点将B样条曲线分成多个曲线段，每个曲线段都定义在一个节点区间内，并且每个曲线段都是p次贝塞尔曲线。

虽然$N_{i,p}(u)$看起来像$B_{n,i}(u)$，但B样条基函数的次数需要人为指定，而贝塞尔基函数的次数取决于控制点的数量。

要改变B样条曲线的形状，可以修改以下 一个或多个控制参数：控制点的位置、节点的位置和曲线的次数。

三种B样条曲线

如果节点向量没有任何特殊结构，生成的曲线将不会接触控制折线的第一条和最后一条边，如下图左侧所示。这种类型的B样条曲线被称为开放(Open)B样条曲线。

Clamped B样条曲线

我们可能想强制曲线使得它分别与第一个控制点和最后一个控制点的第一边和最后一边相切，像贝塞尔曲线那样。为此，第一个节点和最后一个节点必须具有$p+1$重重复度。这就产生了所谓的**$clamped-B$样条曲线**。见下面中间图。

通过重复一些节点和控制点，生成的曲线可以是闭合(Closed)的。在这种情况下,生成曲线的起点和终点连接在一起形成一个闭合环，如右图所示。

在本文中，我们主要讨论$clamped-B$样条曲线

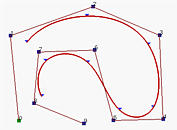
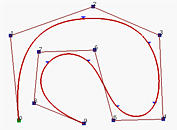
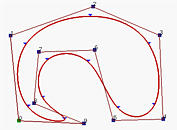
上述图形有$n+1$个控制点且$n=9$及$p=3$。那么，$m$必须是13，所以节点向量有14个节点。为了获得$clamped$效果，前$p+1=4$个和最后4个节点必须是相同的。其余的$14-(4+4)=6$个节点可以在定义域内的任何位置。

上图中该曲线是由节点向量$U=\{0,0,0,0,0.14,0.28,0.42,0.57,0.71,0.85,1,1,1,1\}$生成的。除了前四个和最后四个节点外，中间的节点几乎是均匀分布的。上图中还显示了每个节点区间上相应的曲线段，其中小三角形就是节点点。

Tips:

我们使用开（$open$）， $clamped$ 和闭（$closed$）来描述三种类型的B样条曲线。但是，不是每一个作者都会使用相同的术语，并没有一个标准用法的共识。例如，有些作者会使用 $floating, open 和 periodic$ 来称呼 开（$open$）, $clamped$ 和 闭（$closed$）曲线。其他有些作者会使用 “$periodic$” 来称呼一个有均匀节点序列的开（$open$）B样条曲线。

开（Open）B样条曲线

前面提到，如果节点向量中第一个和最后一个节点的重复度不是$p+1$(其中$p$是B样条曲线的次数)，那么曲线将不会在第一个和最后一个控制点处分别与第一条边和最后一条边相切。该曲线是一条开放（$Open$）B样条曲线。

在前面我们展示了一个基函数的计算示例，使用的节点向量为$U = \{0, 0.25, 0.5, 0.75, 1\}$(其中$m=4$)，如果基函数的次数为1(即$p=1$)，那么有三个基函数$N_{0,1}(u)、N_{1,1}(u)$和$N_{2,1}(u)$，如下图所示：

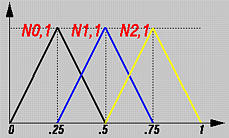
由于这个节点向量没有$clamped$，所以第一个和最后一个节点区间(即$[0,0.25)$和$[0.75,1)$)只有一个非零基函数，而第二个和第三个节点区间(即$[0.25,0.5)$和$[0.5,0.75)$)有两个非零基函数。

回顾B样条基函数的重要性质，在节点区间$[u_i,u_{i+1})$上,最多有$p+1$个p次非零基函数。因此，在这个例子中,节点区间$[0,0.25)$和$[0.75,1)$没有"完全支持"的基函数，即没有基函数定义。因此，对于次数为$p$的曲线，区间$[u_0,u_p)$和$[u_{m-p},u_m]$将不会有"完全支持"的基函数，当B样条曲线为(Open)开曲线时，该区间会被忽略。

因此，我们有结论：对于开放的B样条曲线,其定义域为$[u_p,u_{m-p}]$。

考虑一条由14个控制点($n=13$)定义的6次B样条曲线($p=6$)。节点的数量是21(即$m=n+p+1=20$)。如果节点向量是均匀的,节点为$0、0.05、0.10、0.15、...、0.90、0.95$和$1.0$。开放曲线的定义域为$[u_p,u_{n-p}]=[u_6,u_{14}]=[0.3,0.7]$，并且不与第一条边和最后一条边相切。下图左侧显示了曲线,右侧给出了B样条基函数。

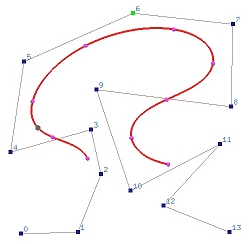
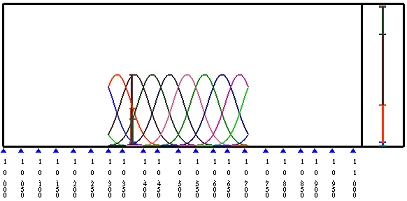
虽然两端的一些节点区间未被使用，但B样条曲线仍然由所有控制点定义。在前面我们有结论：曲线在节点区间$[u_i,u_{i+1})$上,最多有$p+1$个非零基函数$N_{i-p,p}(u)、N_{i-p+1,p}(u)、...、N_{i,p}(u)$。因此,在$[u_p,u_{i+1})$上有$p+1$个非零函数:$N_{0,p}(u)、N_{1,p}(u)、...、N_{p,p}(u)$。

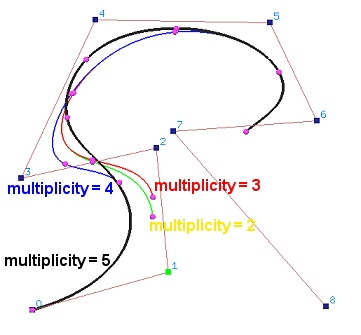
用一个例子来说明($open$)开放曲线和$clamped$曲线之间的变化：

假设我们有一个由9个控制点(即$n=8$)和均匀节点向量$\{0,1/13,2/13,3/13,...,12/13,1\}$定义的4次开放B样条曲线。如果我们将第2个节点$1/13$改为$0$，使$0$成为重复节点，则曲线为图中的黄色曲线。

变化后的曲线和原来的曲线几乎相同。现在，我们将第3个节点$2/13$改为$0$(重复度为3)，结果就是红色曲线。将第四个节点$3/13$改为$0$(重复度为4)，得到的曲线就是蓝色的。

如图所示，这三条(Open)开放曲线彼此并无太大差异。现在，将第5个节点$4/13$改为$0$。由于$0$现在是5重节点(即$p+1$)，曲线不仅通过第一个控制点，而且与控制折线的第一条边相切(即$clamped$效果)。从图中可以看到，将曲线的第一个端点移到第一个控制点，曲线的形状会剧烈地变化，如果我们把最后5个节点值修改为1也会发生同样变化。

闭合（Closed）B样条曲线

有许多方法可以生成闭合曲线，常用的方法是(包裹)wrapping控制点或(包裹)wrapping节点矢量。

wrapping控制点

假设我们要构造一条由 $n + 1$ 个控制点 $P_0, P_1, ..., P_n$ 定义的 $p$ 次闭合B样条曲线 $C(u)$。节点的数量是 $m + 1$，其中 $m = n + p + 1$。下面是构造过程：

1. 设计一个均匀节点序列，包含 $m + 1$ 个节点: $u_0 = 0, u_1 = \frac{1}{m}, u_2 = \frac{2}{m}, ..., u_m = 1$。注意，($Open$)开曲线的定义域是 $[u_p, u_{n-p}]$
2. wrapping前 $p$ 个和最后 $p$ 个控制点：令 $P_0 = P_{n-p+1}, P_1 = P_{n-p+2}, ..., P_{p-2} = P_{n-1}$ 和 $P_{p-1} = P_n$。如下图所示：

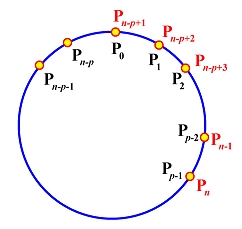
在连接点 $C(u_p) = C(u_{n-p})$ 处，构造的曲线是 $C^{p-1}$ 连续的。

下面的例子中，图 (a) 显示了一条由 10 个($n = 9$)控制点和均匀节点矢量定义的 3 次开放 B 样条曲线。在该图中，控制点对 0 和 7、1 和 8、2 和 9 彼此靠近，以说明构造过程。

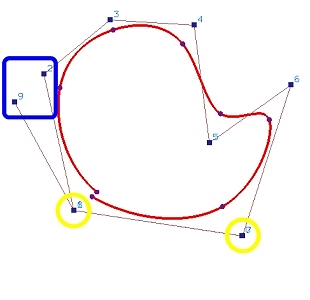
图 (b) 显示将控制点 0 和 7 设为相同时的结果。曲线的形状没有发生太大变化。图 © 显示将控制点 1 和 8 设为相同。很明显，曲线的第一个点和最后一个点之间的间隙变小了。最后，当控制点 2 和 9 设为相同时，如图 (d) 所示，曲线变成了闭合曲线。

(a)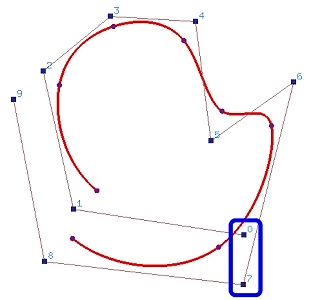
(b)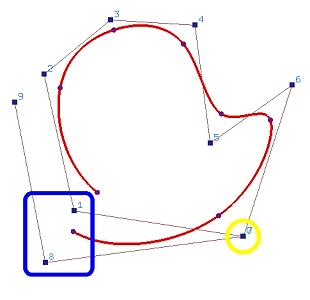
©
(d)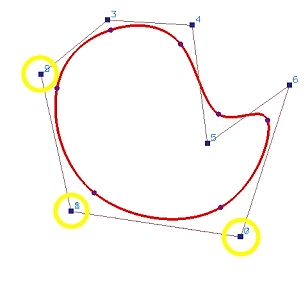

wrapping节点

构造闭合 B 样条曲线的另一种方法是$wrapping$节点。假设我们要构造由 $n + 1$ 个控制点 $P_0, P_1, ..., P_n$ 定义的 $p$ 次闭合 B 样条曲线 $C(u)$。下面是构造过程:

1. 添加一个新的控制点 $P_{n+1} = P_0$。因此，控制点的数量是 $n + 2$。

2. 找到一个合适的 $n + 1$ 个节点的节点序列 $u_0, u_1, ..., u_n$。这些节点不一定是均匀的，

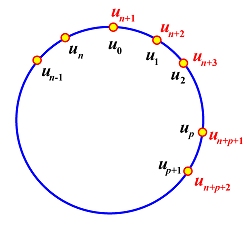
3. 添加 $p + 2$ 个节点，并$wrapping$前 $p + 2$ 个节点: $u_{n+1} = u_0, u_{n+2} = u_1, ..., u_{n+p} = u_{p-1}, u_{n+p+1} = u_p, u_{n+p+2} = u_{p+1}$，如下图所示。这样，我们就有 $n + p + 2 = (n + 1) + p + 1$ 个节点。

   

4. 使用上述 $n + 1$ 个控制点和 $n + p + 2$ 个节点上定义的 $p$ 次开放 B 样条曲线 $C(u)$ 是一条在连接点 $C(u_0) = C(u_{n+1})$ 处具有 $C^{p-1}$ 连续性的闭合曲线。注意，这条闭合曲线的定义域是 $[u_0, u_{n+1}]$。

B样条曲线重要属性

B样条曲线与Bézier曲线有很多相同的性质，因为前者是后者更泛化的形式。下面的列表显示了B样条曲线的一些最重要的性质。

我们假设B样条曲线$C(u)$的次数为$p$，由$n + 1$个控制点和一个节点向量$U = {u_0, u_1, ...., u_m}$定义，其中前$p+1$个和后$p+1$个节点是$clamped$的(即$u_0 = u_1 = ... = u_p$和$u_{m-p} = u_{m-p+1}= ... =u_m$)

B样条曲线$C(u)$是一个分段曲线，每个组成部分都是$p$次的曲线。

前面提到过，$C(u)$可以看作是在每个节点区间上定义的曲线段的并集。

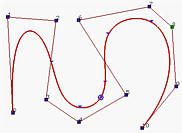
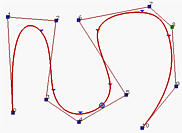
在下图中，其中$n = 10$，$m = 14$和$p = 3$，前四个节点和后四个节点是$clamped$的，中间7个节点均匀分布。有8个节点区间，每个区间都对应一个曲线段。在下面的左图中，这些节点点显示为三角形。这个良好性质使得我们可以以更低次多项式来设计复杂形状。

例如，下面的右图显示了具有相同控制点的Bézier曲线。尽管其次数为10，但它仍然无法很好地跟随控制多边形！

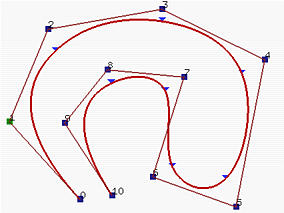
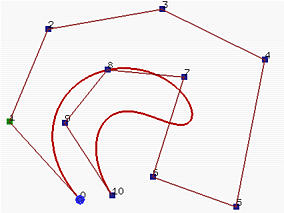
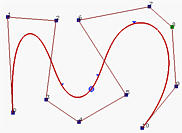
一般来说，次数越低，B样条曲线越接近其控制多边形。以下图形都使用相同的控制多边形，节点是$clamped$的并且均匀分布。第一幅图的次数为7，中间的次数为5，右图的次数为3。因此，随着次数的降低，生成的B样条曲线越接近其控制多边形。

B样条曲线满足等式$m = n + p + 1$

因为每个控制点需要一个基函数，基函数的数量满足$m = n + p + 1$。

clamped B样条曲线$C(u)$通过两个端点控制点$P_0$和$P_n$

基函数$N_{0,p}(u)$是控制点$P_0$的系数，并且在$[u_0,u_{p+1})$上非零。由于对于固定的B样条曲线，$u_0 = u_1 = ... = u_p = 0$，$N_{0,0}(u)$，$N_{1,0}(u)$，…，$N_{p-1,0}(u)$为零，只有$N_{p,0}(u)$非零（回忆三角形计算格式）。因此，如果$u = 0$，那么$N_{0,p}(0)$为1且$C(0) = P_0$。相似地可得到$C(1) = P_n$

强凸包性质：样条曲线包含在控制折线的凸包内

具体地说：如果$u$在节点区间$[u_i,u_{i+1})$中，那么$C(u)$在控制点$P_{i-p}$，$P_{i-p+1}$，…，$P_i$的凸包中。

如果$u$在节点区间$[u_i, u_{i+1})$中，那么只有$p+1$个基函数（即，$N_{i,p}(u)$，… ，$N_{i-p+1,p}(u)$，$N_{i-p,p}(u)$）在这个节点区间上非零。由于$N_{k,p}(u)$是控制点$P_k$的系数，只有$p+1$个控制点$P_i$，$P_{i-1}$，$P_{i-2}$，…，$P_{i-p}$具有非零系数。

由于在这个节点区间上基函数是非零的并且和为1，它们的"加权"平均数$C(u)$，必须位于由控制点$P_i$，$P_{i-1}$，$P_{i-2}$，…，$P_{i-p}$定义的凸包中。"强"的含义是，虽然$C(u)$仍然位于所有控制点定义的凸包中，但曲线的每一段位于一个更小的凸包中。

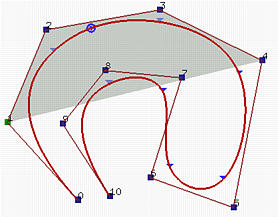
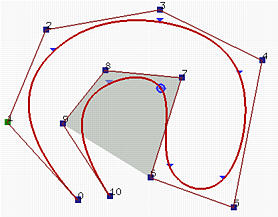
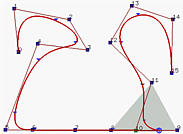
上图两个B样条曲线有11个控制点（即，$n = 10$），次数为3（即，$p=3$）和15个节点（$m = 14$），其中前四个和后四个节点是$clamped$的。因此，节点区间的数量等于曲线段的数量，节点向量是：

左图中当$u$在节点区间$[u_4, u_5) = [0.12,0.25)$上时，对应的点（即$C(u)$）在第二个曲线段中，因此，这个节点区间上有$p+1 = 4$个基函数非零（即，$N_{4,3}(u)$，$N_{3,3}(u)$，$N_{2,3}(u)$和$N_{1,3}(u)$）和对应的控制点是$P_4$，$P_3$，$P_2$和$P_1$，阴影区域是由这四个点定义的凸包，很明显，$C(u)$位于这个凸包中。

右图中的B样条曲线的定义方式相同，$u$在$[u_9, u_10) = [0.75,0.87)$中，非零的基函数是$N_{9,3}(u)$，$N_{8,3}(u)$，$N_{7,3}(u)$和$N_{6,3}(u)$，对应的控制点是$P_9$，$P_8$，$P_7$和$P_6$。

因此，当$u$从0移动到1，每当穿过一个节点区间时，就会有一个基函数变为零，同时一个新的非零基函数变得有效。

结果是，系数变为零的控制点会离开当前凸包的定义，而被一个新的系数变为非零的控制点所代替

局部修改特性：改变控制点$P_i$的位置只影响区间$[u_i, u_{i+p+1})$上的曲线$C(u)$

回想一下，$N_{i,p}(u)$在区间$[u_i, u_{i+p+1})$上非零。如果$u$不在这个区间内，$N_{i,p}(u)Pi$ 项对计算$C(u)$没有贡献，因为$N_{i,p}(u)$是零。另一方面，如果$u$在这个区间内，$N_{i,p}(u)$是非零的。如果$P_i$改变其位置，$N_{i,p}(u)P_i$就会改变，因此$C(u)$就会改变。

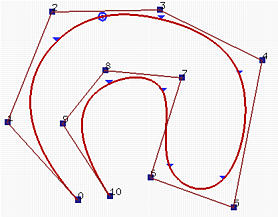
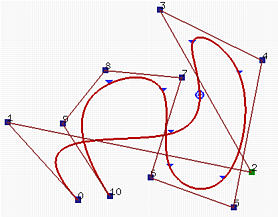
上述B样条曲线与前面的凸包示例中定义的参数相同。

我们移动控制点$P_2$。这个控制点的系数是$N_{2,3}(u)$，这个系数在区间$[u_2, u_{2+3+1}) = [u_2, u_6) = [0,0.37)$上是非零的。由于$u_2 = u_3 = 0$，只对应于$[u_3, u_4)$（，$[u_4, u_5)$和$[u_5, u_6)$的三个曲线段将受到影响。右图显示了将$P_2$移动到右下角的结果。如你所见，只有第一、第二和第三个曲线段改变了它们的形状，其他曲线段则不受影响。

这种局部修改特性对于曲线设计非常重要，因为我们可以在不修改全局形状的情况下，局部修改曲线。如果需要微调曲线形状，可以插入更多的节点（因此会有更多的控制点），以便受影响的区域可以被限制在一个很小的区域。

$C(u)$在重复度为$k$的节点处是$C^{p-k}$连续的

如果$u$不是一个节点，$C(u)$在曲线段的中间位置，则该位置处是无穷可微的。如果$u$是$N_{i,p}(u)$非零域中的一个节点，节点处只是$C^{p-k}$连续的，所以整个曲线$C(u)$也是$C^{p-k}$连续的。

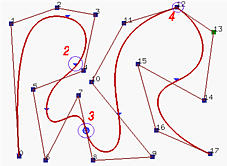
上述B样条曲线有18个控制点（即，$n = 17$），次数为4，clamped节点向量如下：

$u_6$是一个双节点，$u_9$是一个三重节点，$u_{13}$是一个四重节点。因此，$C(u)$在任何不是节点的点上是$C^4$连续的，在所有简单节点上是$C^3$连续的，在$u_6$上是$C^2$连续的，在$u_9$上是$C^1$连续的，在$u_{13}$上是$C^0$连续的。

曲线上节点都用小三角形标记。多重节点用圆圈和它们的重数标记。要直接看出$C^4$，$C^3$甚至$C^2$连续性之间的差异是很难的。对于$C^1$连续的情况，相应的点位于一条控制折线边上，而$C^0$的情况则强制曲线通过一个控制点。

变差减小性质

如果曲线在一个平面（或空间）中，这意味着没有直线（或平面）与B样条曲线相交的次数多于它与曲线的控制多边形相交的次数。

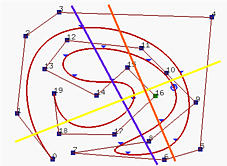
在上图中，蓝线与控制多边形和B样条曲线都相交6次，而黄线也与控制多边形和B样条曲线相交5次。然而，橙线与控制多边形相交6次，与曲线相交4次。

Bézier曲线是B样条曲线的特例。

如果$n = p$（即，B样条曲线的次数等于$n$，控制点的数量减1），并且有$2(p + 1) = 2(n + 1)$个节点，其中前$p + 1$个节点和后$p+1$个节点在端点$clamped$，那么B样条曲线就退化成$Bézier$曲线。

仿射不变性

如果对B样条曲线应用一个仿射变换，结果可以从其控制点的仿射图像构造出来，这是一个非常好的性质。

当我们想要对B样条曲线应用几何甚至仿射变换时，这个性质表明我们可以将变换应用到控制点，这是相当容易的，一旦得到了变换后的控制点，变换后的B样条曲线就是由这些新点定义的，因此，我们不必对曲线进行变换。

使用B样条曲线的优势

B样条曲线需要比Bézier曲线更多的控制信息（即曲线的次数和节点向量）和更复杂的理论。但是，它也有更多的优点。

• B样条曲线可以是Bézier曲线。
• B样条曲线满足Bézier曲线具有的所有重要性质。
• B样条曲线提供比Bézier曲线更多的控制灵活性。
  例如，B样条曲线的次数与控制点的数量是分开的。我们可以使用低次数的曲线并仍然保持大量的控制点。
  我们可以改变控制点的位置而不会全局改变整个曲线的形状（局部修改特性）。
  由于B样条曲线满足强凸包性质，它们具有更精细的形状控制。此外，还有可以通过改变节点来设计和编辑曲线形状。

B样条曲线仍然是多项式曲线，多项式曲线不能表示许多有用的简单曲线，如圆和椭圆。因此，需要一种更加泛化的曲线，NURBS应运而生， 后面会详细介绍NURBS曲线。

B样条曲线系数的计算

我们说明一种简单的方法来计算B样条曲线的系数：

给定一个由$n+1$个控制点$P_0$，$P_1$，…，$P_n$定义的$p$次$clamped$ B样条曲线，有$m+1$个节点$u_0=u_1=...=u_p=0$，$u_{p+1}$，$u_{p+2}$，…，$u_{m-p-1}$，$u_{m-p}=u_{m-p+1}=...= u_m=1$

对于任何给定在$[0,1]$上的 $u$，我们想要计算系数$N_{0,p}(u)$，$N_{1,p}(u)$，…，$N_{n,p}(u)$。一种简单的方法是使用以下递归关系：

$$N_{i,0}(u)=\left\{\begin{array}{ll}1&\mathrm{if~}u_i\leq u<u_{i+1}\\\\0&\mathrm{otherwise}\end{array}\right.$$

$$N_{i,p}(u)=\frac{u-u_{i}}{u_{i+p}-u_{i}}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)$$

然而，这是一个非常耗时的过程
为了计算$N_{i,p}(u)$，我们需要计算$N_{i,p-1}(u)$和$N_{i+1,p-1}(u)$
为了计算$N_{i,p-1}(u)$，我们需要计算$N_{i,p-2}(u)$和$N_{i+1,p-2}(u)$。
为了计算$N_{i+1,p-1}(u)$，我们需要$N_{i+1,p-2}(u)$和$N_{i+2,p-2}(u)$。
$N_{i+1,p-2}(u)$出现了两次，因此，它的递归计算也将被重复。随着递归深入，将会出现更多的重复计算。这和之前讲过的贝塞尔曲线的$de Casteljau$算法的递归版本非常相似。因此，这种方式计算速度非常慢。

有一个简单的方法，假设$u$在节点区间$[u_k,u_{k+1})$中，B样条基函数的一个重要性质表明，最多有$p+1$个$p$次基函数在$[u_k,u_{k+1})$上非零，即：$N_{k-p,p}(u)$，$N_{k-p+1,p}(u)$，$N_{k-p+2,p}(u)$，…，$N_{k-1,p}(u)$，$N_{k,p}(u)$。根据定义，在$[u_k,u_{k+1})$上唯一非零的0次基函数是$N_{k,0}(u)$，因此，从$N_{k,0}(u)$开始计算系数，形成如下所示的"扇形"三角形形式：

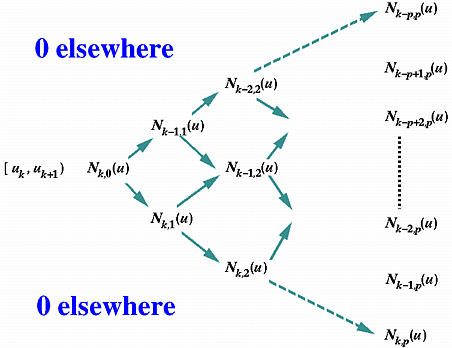
在节点区间$[u_k,u_{k+1})$上，$N_{k,0}(u) = 1$，而其他0次B样条基函数在$[u_k,u_{k+1})$上是零，我们可以从$N_{k,0}(u)$开始，计算1次基函数$N_{k-1,1}(u)$和$N_{k,1}(u)$，得到这两个值后，我们可以计算2次基函数$N_{k-2,2}(u)$，$N_{k-1,2}(u)$和$N_{k,2}(u)$。重复这个过程，直到所有$p+1$个非零系数被计算出来。

在上面的计算过程中，"内部"的值，如$N_{k-1,2}(u)$，有一个西北方向的前驱（即，$N_{k-1,1}(u)$）和一个西南方向的前驱（即，$N_{k,1}(u)$）；
上述三角形的东北方向边界上的值，如$N_{k-1,1}(u)$，只有一个西南方向的前驱（即，$N_{k,0}(u)$）；
而这个三角形的东南方向边界上的值，如$N_{k,2}(u)$，只有一个西北方向的前驱（即，$N_{k,1}(u)$）。
因此，位于东北方向（或东南方向）边界上的值使用定义中的递归关系的第二个（或第一个）项。只有内部的值使用两个项。基于这个观察，我们有以下的算法：

这个算法可能并不是最有效的，但它的目的是以直观易懂的方式阐述思想。

我们有一个数组 $N[ ]$，它用来存储所有的中间结果和最终结果。对于一个给定的次数 $d$，数组中的元素 $N[i]$ 保存了 $N_{i,d}(u)$ 的值。最后，数组中的元素 $N[k-d]$, $N[k-d+1]$, …, $N[k]$ 会包含非零系数。

计算过程从 $d=1$ 开始，因为我们知道唯一的非零基函数是 $N_{k,0}(u)$，这个基函数只在节点区间 $[u_k,u_{k+1})$ 上非零。然后，我们通过一个外循环让次数 $d$ 从 1增加到 $p$。

在 begin 后面的第一次赋值中，我们只使用了一个项（即，三角形的西南项，$N_{k-d+1,d-1}(u)$）来计算 $N_{k-d,d}(u)$。接着，内部的 for 循环用来计算"内部"的项。最后，在外循环的最后一个语句中，我们只使用了一个项（即，三角形的西北项，$N_{k,d-1}(u)$）来计算 $N_{k,d}(u)$。

一个特殊案例: Bézier曲线是B样条曲线的特殊情况

如果我们有$2n+2$个节点，其中$u_0 = u_1 = ... = u_n = 0$，并且$u_{n+1} = u_{n+2} = ... = u_{2n+1} = 1$（即，前$n+1$个节点为0，接下来的$n+1$个节点为1），那么$n$次B样条基函数是什么？

由于每个$u$都在$[0,1] = [u_n, u_{n+1}]$范围中，所以非零的n阶基函数是：$N_{0,n}(u), N_{1,n}(u), ..., N_{n,n}(u)$

回顾一下B样条基函数的定义如下：

$$\begin{array}{rcl}N_{n,0}(u)&=&\left\{\begin{array}{ll}1&\text{if }n\in[u_n,u_{n+1})=[0,1)\\\\0&\text{otherwise}\end{array}\right.\\N_{i,n}(u)&=&\frac{u-u_i}{u_{i+n}-u_i}N_{i,n-1}(u)+\frac{u_{i+n+1}-u}{u_{i+n+1}-u_{i+1}}N_{i+1,n-1}(u)\end{array}$$

由于唯一的非零0阶基函数是$N_{n,0}(u)$，所以索引$i$只能在0和$n$的范围内。因此，$u_i$是零，$u_{i+n}$和$u_{i+n+1}$是1。因此，上述第二个等式可以重写为：

$$N_{0,n}(u)=(1-u)N_{1,n-1}(u)$$

$$N_{n,n}(u)=uN_{n,n-1}(u)$$

$$N_{i,n}(u)=uN_{i,n-1}(u)+(1-u)N_{i+1,n-1}(u)$$

如果我们按照之前讨论的方式，将$N_{0,n}(u), N_{1,n}(u), ..., N_{n,n}(u)$的计算组织成一个三角形，我们会得到以下的图。在这个图中，每个向东北（或者，向东南）的箭头表示将$1-u$（或者，$u$）乘以箭头尾部的项。注意，计算中有$n$次迭代过程，每个迭代仅获取一列。因此，$N_{n,0}(u)$对$N_{0,n}(u)$的贡献是$(1-u)^n$，$N_{n,0}(u)$对$N_{n,n}(u)$的贡献是$u^n$。

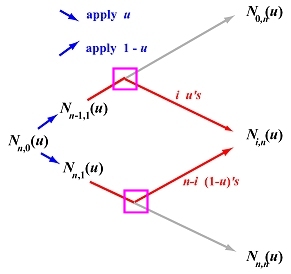
现在，考虑一般项 $N_{i,n}(u)$的计算：

我们可以通过"路径计数（$path-counting$）"的方式，这是一种用于证明$de Casteljau$算法正确性和计算$Bézier$曲线高阶导数的方法，用来确定 $N_{n,0}(u)$ 对 $N_{i,n}(u)$ 的计算贡献。

每条从 $N_{n,0}(u)$ 到 $N_{i,n}(u)$ 的路径都会经过 $n$ 个箭头，其中 $i$ 个箭头指向东南，剩下的 $n-i$ 个箭头指向东北。这些箭头表示将 $1-u$（或者，$u$）乘以箭头尾部的项。因此，$N_{n,0}(u)$ 对单个路径上的 $N_{i,n}(u)$ 的贡献是 $u^i(1-u)^{n-i}$。

从 $N_{n,0}(u)$ 到 $N_{i,n}(u)$ 的路径总数是 $C(n,i)$，也就是说，路径的数量等于在$ n $个位置中放置$i$ 个向东南的箭头时，不同放置方式的数量。剩余的$n-i$个位置则是向东北的箭头。这$ n$个箭头描述了从 $N_{n,0}(u)$ 到 $N_{i,n}(u)$ 的单个路径。

由于每条路径对计算贡献了 $u^i(1-u)^{n-i}$，并且有 $C(n,i)$ 条路径，所以 $N_{n,0}(u)$ 对 $N_{i,n}(u)$ 的总贡献是：

$$C(n,i)u^i(1-u)^{n-i}=\frac{n!}{i!(n-i)!}u^i(1-u)^{n-i}=B_{n,i}(u)$$

这正是$n$阶的第$i$个Bézier基函数。因此，我们得出以下结论：

如果前$n+1$个节点等于0（或者，最后$n+1$个节点等于1），那么$n$阶的第$i$个B样条基函数与所有在0和$n$范围内的第$i$个Bézier基函数相同。

因此，Bézier基函数是B样条基函数的特殊情况，Bézier曲线是B样条曲线的特殊情况。

B样条曲线移动控制点

移动控制点是改变B样条曲线形状的最直接的方式。由于B样条曲线的局部修改特性，改变控制点$P_i$的位置只会影响曲线$C(u)$在区间$[u_i, u_i+p+1)$上部分，其中$p$是B样条曲线的次数。

实际上，曲线形状的改变是在控制点被移动的的方向上进行的平移。更准确地说，如果控制点$P_i$被移动到某个方向的新位置$Q_i$，那么点$C(u)$在$[u_i, u_i+p+1)$的部分，将会在沿着从$P_i$到$Q_i$的同一方向上移动。但是，曲线上不同点移动的距离是不同的。

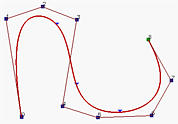
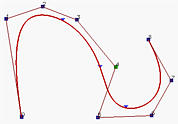
下图中，控制点$P_4$从左图的位置移动到中图的新位置，最后移动到右图的最终位置，对应于节点（用小三角形标记）的那些点在同一方向上移动。

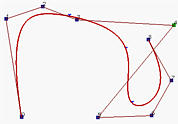
具体分析一下：

假设$C(u)$是一个给定的次数为$p$的B样条曲线，定义如下：

$$\mathbf{C}(u)=\sum_{i=0}^nN_{i,p}(u)\mathbf{P}_i$$

让控制点$P_i$移动到新的位置$P_i + v$。那么，新的$p$次B样条曲线$D(u)$如下：

$$\mathrm{D}(u)=\sum_{k=0}^{i-1}N_{k,p}(u)\mathbf{P}_{k}+N_{i,p}(u)(\mathbf{P}_{i}+\mathbf{v})+\sum_{k=i+1}^{n}N_{k,p}(u)\mathbf{P}_{k}$$

$$=\sum_{k=0}^nN_{k,p}(u)\mathbf{P}_k+N_{i,p}(u)\mathbf{v}$$

$$=\mathbf{C}(u)+N_{i,p}(u)\mathbf{v}$$

因此，新的曲线$D(u)$只是原始曲线$C(u)$加上一个平移向量$N_{i,p}(u)\mathbf{v}$。
由于$N_{i,p}(u)$在区间$[u_i,u_i+p+1)$上是非零的，如果$u$不在这个区间，这个"平移"项就是零。因此，移动一个控制点只会影响给定曲线在$[u_i,u_i+p+1)$区间的部分。

下面左图的曲线是一个由13个控制点（即$n = 12$）和18个节点（即$m = 17$）定义4次B样条曲线（即$p = 4$）。这18个节点都是简单的，并定义了一个$clamped$曲线（即$u_0 = u_1 = u_2 = u_3 = u_4 = 0$和$u_{13} = u_{14} = u_{15} = u_{16} = u_{17} = 1$）。剩下的节点定义了9个节点区间，因此如图所示有9个曲线段。这9个节点区间定义如下：

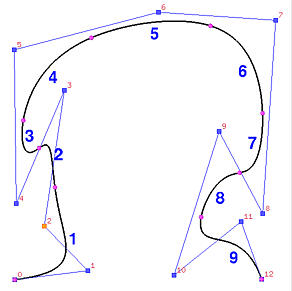
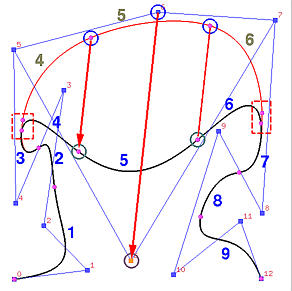
移动$P_6$，结果显示在上面的右图中。如图所示，曲线在同一方向上移动。$P_6$的系数是$N_{6,4}(u)$，它在$[u_6, u_{11})$上是非零的。因此，移动$P_6$会影响曲线段3、4、5、6和7，而曲线段1、2、8和9不受影响。

强凸包性质的应用

回忆强凸包性质：如果$u$位于$[u_i,u_{i+1})$，那么$C(u)$位于由控制点$P_i, P_{i-1}, ..., P_{i-p+1}, P_{i-p}$定义的凸包内。我们可以利用这个性质达到以下效果：

强制曲线段变为线段：让$p+1$个相邻的控制点共线。

如果$u$位于节点区间$[u_i,u_{i+1})$，那么$C(u)$位于由$p+1$个控制点$P_i, P_{i-1}, ..., P_{i-p+1}, P_{i-p}$定义的凸包内。由于这对该区间内的所有$u$都成立，所以这个节点区间上的曲线段完全位于这个凸包内。如果所有这些$p+1$个控制点都共线（即，在一条直线上），那么凸包就会塌陷到一条线段，包含的曲线段也会如此。

**因此，节点区间$[u_i,u_{i+1})$上的曲线段变为一条线段。**在这种情况下，只有这个曲线段变为线段。其他曲线段仍然是非线性的。

(a)	（b)	©
(d)	(e)	(f)

让我们看一个例子

上图中的曲线是由$n = 15$（即，16个控制点），$p = 3$（度数3）和$m = 19$（即，20个节点）定义的。注意，前四个和后四个节点是$clamped$的。

图（a）是给定的B样条曲线，我们让$P_9, P_8, P_7$和$P_6$共线。因此，$[u_9,u_{10})$上的曲线段位于由$P_9, P_8, P_7$和$P_6$定义的凸包内。由于这个凸包是一条线段，曲线段也必须是一条线段。由于前四个节点是$clamped$的，因此前三个节点区间不存在。由于$[u_9,u_{10})$是第7个节点区间，因此第7段塌陷到线段$P_7P_8$。这由图（b）、（c）和（d）所示。

但是，为什么$[u_9,u_{10})$上的曲线段是唯一塌陷的曲线段呢？见图（b），阴影区域是$u$进入$[u_9,u_{10})$之前的凸包。这个凸包由控制点$P_8, P_7, P_6$和$P_5$定义，它还不是线段。一旦$u$进入$[u_9,u_{10})$，曲线段就会塌陷（图（c））。$u$离开$[u_9,u_{10})$后，立即出现一个新的凸包（图（d））。

图（e）有$P_5$与其后继四个控制点共线。曲线包含一个更多的线段。图（f）有$P_{10}$与其前五个控制点共线，然而，由于控制点$P_{10}$被移动到$P_8$和$P_9$之间的位置。这将使相应的曲线段的一部分成为直线

强制B样条曲线通过某个控制点：让$p$个相邻的控制点相同。

考虑控制点$P_i$。由于节点区间$[u_i, u_{i+1})$上的曲线段完全位于由$P_i, ..., P_{i-p+1},P_{i-p}$定义的凸包内，如果我们让前$p$个控制点相同（即，$P_i = P_{i-1} = ... = P_{i-p+1}$），凸包就会塌陷到线段$P_{i-p}P_i$，曲线必须通过$P_i$。

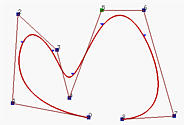
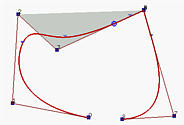
上图左侧的曲线是3次的。如果将$P_5$移动并与$P_6$相同，曲线会更接近$P_6$，但还没有通过它，如中间的图所示。注意，这次移动，曲线段的数量没有改变；然而，靠近$P_5$的小三角形标记被移动更接近$P_6$。如果将$P_4$移动并与$P_6 = P_5$重合，曲线将通过$P_6$，且曲线上对应节点的点因为移动而与控制点$P_4$重合。

强制B样条曲线与控制折线的一条边相切

让$P_{i-p}, P_{i-p+1} = P_{i-p+2} = .... = P_{i-1} = P_i$及$P_{i+1}$共线。

在上面，如果让$p$个相邻的控制点重合，则在重合的控制点上，连续性为$C^0$，因为曲线有一个尖点（参见上面右图）。但是，B样条曲线在简单节点处是$C^{p-1}$连续的，在其他地方无限可微，曲线在边$P_{i-p}P_i$上的控制点$P_i$处连续性为$C^{p-1}$连续，并且在边$P_iP_{i+1}$上的控制点$P_i$处连续性也为$C^{p-1}$连续。

因此，如果我们让控制点$P_{i-p}, P_i$和$P_{i+1}$共线，只要两个相邻的曲线段在节点处没有尖点，它们在$P_i$处就是$C^{p-1}$连续的。

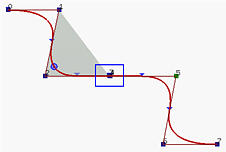
在上面的图形中，曲线的次数是 2。如果我们让控制点2、3、4和5共线，而3和4重合，我们可以得到右图。共线性确保曲线段位于直线上，而重合的控制点保证了$C^{3-1} = C^2$连续

B样条曲线修改节点

由于B样条曲线是由多个曲线段组成的，每个曲线段都在一个节点区间上定义，所以修改一个或多个节点的位置会改变相应的曲线段和节点区间，从而改变曲线的形状。

下图描述了修改单个节点的效果。这是一个6次的B样条曲线，有17个节点，前7个和后7个节点在端点处是$clamped$，而内部节点是0.25、0.5和0.75。初始曲线显示在左边。

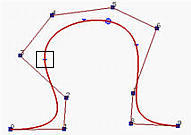
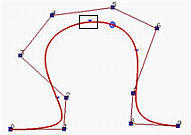
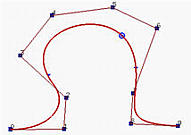
如果节点0.25移动到0.1，曲线的形状会改变，原来的$C(0.25)$会向下移动到一个新的位置。

如果节点0.5移动到0.1，使得节点0.1变成一个双重节点（重数为2），曲线的形状会向左移动，但是$C(0.1)$会向上移动到一个接近原来点的位置（即，原来的$C(0.25)$），结果显示在右图。

此外，尽管我们在0.1处有一个双重节点，另一个节点在0.75处，这两个节点不均匀地将域$[0,1]$划分为三个节点区间，但B样条曲线被它们相应点几乎均匀地划分。

下图显示了三条曲线的形状变化，每条曲线都由10个（$n=9$）控制点定义，并且曲线是6次的。它们的内部节点向量是$(0.25,0.5,0.75)$ - 红色曲线，$(0.25,0.25,0.75)$ - 蓝色曲线，和$(0.25,0.25,0.25)$ - 黑色曲线。

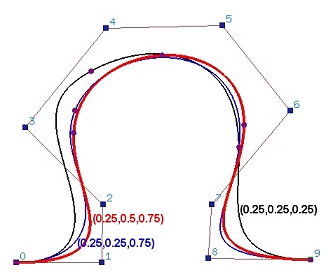
实际经验表明，修改节点位置既不可预测也不令人满意，因为不清楚B样条曲线的形状如何响应节点向量的变化，通过改变节点来修改B样条曲线的形状通常是不令人满意的，很难达到设计目的

关于多重节点的评注

多重节点有助于生成期望的结果。回忆一下我们之前讨论过的多重节点的一个性质，增加内部节点的重数会减少在此节点处的非零基函数的数量。

实际上，如果这个节点的重数是$k$，那么在这个节点处最多有$p - k + 1$个非零函数。此外，这个节点处的基函数是$C^{p-k}$连续的。
假设一个节点的重数是$p-k$，那么在这个节点处将有$k+1$个非零基函数，曲线上对应的点位于由这些非零基函数的控制点定义的凸包内。如果$k = p - 1$，那么有两个非零函数，对应的凸包是一条线段。

如果$k = p$，那么在这个节点处只有一个非零基函数，只有一个控制点的系数是非零的。因此，曲线会通过这个点！

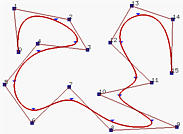
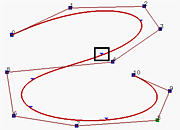
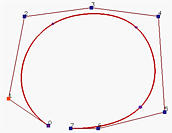
下面的例子说明了这个过程：

（a)	（b)	（c)
（d)	（e)

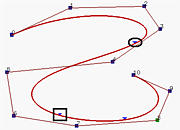
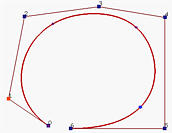
在上图的图（a）中，显示了一个5次B样条曲线，对应于标记的节点被移动到它的前一个节点的位置，创建了一个重数为2的节点，结果在图（b）中，与原始图形没有太大的差别。

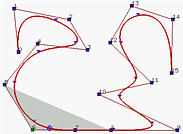
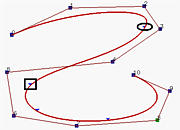
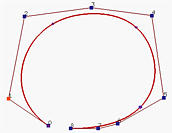
然后，下一个节点（用矩形标记）再次被移动到上一步产生的节点位置（用椭圆标记），创建了一个重数为3的节点。显示在图（c）中，产生的曲线朝控制折线的一条边移动。

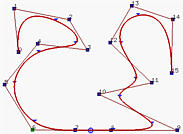
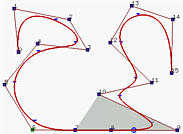
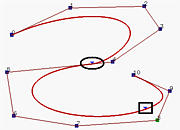
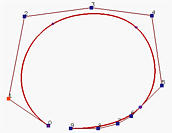
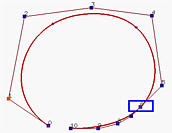
再移动一个节点构建一个重复度4的新节点，这使得相应的点（椭圆标记）位于一条边上。仅剩的一个节点移到与其它节点重叠起来。由于它的重数是5且$p=5$，所以只有一个非零系数，因此使得曲线通过该控制点。如图（e）所示，该控制点是$P_5$。

B样条曲线的导数

尽管B样条曲线比贝塞尔曲线复杂，但它们的导数形式非常相似的。

B样条曲线定义如下：

$$\mathbf{C}(u)=\sum_{i=0}^nN_{i,p}(u)\mathbf{P}_i$$

基函数的导数如下：

$$\frac{\text{d}}{\text{d}u}N_{i,p}(u)=N'_{i,p}(u)=\frac{p}{u_{i+p}-u_i}N_{i,p-1}(u)-\frac{p}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)$$

将这些导数待会原曲线方程，得到如下结果：

$$\frac{\mathrm{d}}{\mathrm{d}u}\mathbf{C}(u)=\mathbf{C}'(u)=\sum_{i=0}^{n-1}N_{i+1,p-1}(u)\mathbf{Q}_i$$

其中$Q_i$定义如下：

$$\mathbf{Q}_i=\frac{p}{u_{i+p+1}-u_{i+1}}(\mathbf{P}_{i+1}-\mathbf{P}_i)$$

因此，B样条曲线的导数是在原始节点向量上的另一个次数为$p - 1$的B样条曲线，并有一组新的$n$个控制点$Q_0, Q_1, ..., Q_{n-1}$

如果原始的$clamped$节点向量是$u_0(p+1), u_{p+1}, ..., u_{m-p-1}, u_m(p+1)$，那么去掉第一个和最后一个节点，使得第一个和最后一个节点的重数变为$p$而不是$p+1$，我们有新的$m - 1$个节点的节点序列$u_0(p), u_{p+1}, ..., u_{m-p-1}, u_m(p)$。

那么，可以证明在原始节点序列计算的$N_{i+1,p-1}(u)$值等于在新的节点序列上的$N_{i,p-1}(u)$值。因此，在新的节点序列上，B样条曲线的导数是以下形式：

$$\frac{\mathrm{d}}{\mathrm{d}u}\mathbf{C}(u)=\mathbf{C}'(u)=\sum_{i=0}^{n-1}N_{i,p-1}(u)\mathbf{Q}_i$$

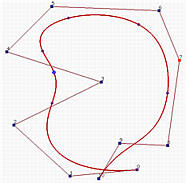
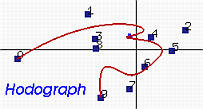
下面左图是一个次数为5的B样条曲线。它的导数曲线，是由新的$n$个控制点定义的次数为$p-1$的B样条曲线，如中间图所示。下面右图中去掉了控制折线。

clamped B样条曲线

我们知道一个$clamped$ B样条曲线通过第一个和最后一个控制点。事实上，它也与其控制折线的第一条和最后一条边相切。上面p次B样条曲线$C(u)$的导数是

$$\frac{\mathrm{d}}{\mathrm{d}u}\mathbf{C}(u)=\mathbf{C}'(u)=\sum_{i=0}^{n-1}N_{i,p-1}(u)\mathbf{Q}_i$$

其节点向量是通过从原始节点序列中删除第一个节点和最后一个节点得到的。因此，第一个（最后一个）节点的重数是$p$，因此，上述$p-1$次B样条曲线是$clamped$的。由于$clamped$ B样条曲线通过其第一个和最后一个控制点，所有，我们有$C'(0) = Q_0$和$C'(1) = Q_{n-1}$。当$i = 0$时，由于$u_0 = .... = u_p = 0$，我们有

$$\mathbf{Q}_0=\frac{p}{u_{p+1}}(\mathbf{P}_1-\mathbf{P}_0)$$

因此，$C'(0)$处的切向量与$P_0P_1$边的方向向量相同，即$C(u)$与第一条边相切。

同理，我们可以得到：

$$\mathbf{Q}_{n-1}=\frac p{1-u_{m-p-1}}\left(\mathbf{P}_n-\mathbf{P}_{n-1}\right)$$

因此，$C(u)$与最后一条边相切。

结论：
clamped B样条曲线通过第一个和最后一个控制点，并且与控制折线的第一条和最后一条边相切。

高阶导数

由于B样条曲线的第一导数是另一个B样条曲线，所以递归计算，可以得到B样条的高阶导数

B样条曲线节点插入

节点插入的含义是在不改变曲线形状的情况下，将一个新的节点添加到现有的节点向量中。这个新的节点可能和一个现有的节点相同，在这种情况下，该节点的重复度增加一。由于基本等式 $m = n + p + 1$，在添加一个新的节点后，$m$ 的值增加一，因此，控制点的数量或曲线的度数也必须增加一。

由于节点增加导致曲线次数的改变会全局改变曲线的形状，因此这种方式不考虑。所以，插入一个新的节点会导致增加一个新的控制点，实际上，会有一些现有的控制点被移除并通过角切割的方式替换为新的控制点。

节点插入是B-样条曲线的最重要的算法之一，因为许多其他算法都基于节点插入。

下面，我们将介绍插入单个节点的方法，然后是多次插入单个节点的方法。

下面的左图显示了一个具有均匀节点的4次$clamped$ B样条曲线，而右图显示了插入新节点 $u = 0.5$ 后的结果。左图还显示了插入前后的控制折线，如图所示，曲线的形状没有改变。但是，控制折线改变了。实际上，四个新的红色控制点替换了原始的控制点 $P_4$，$P_5$ 和 $P_6$，并且三个绿色线段相当于切割了角 $P_4$，$P_5$ 和 $P_6$ 。

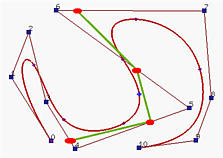
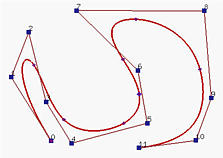
插入单个节点

已知 $n+1$ 个控制点 $P_0, P_1, ..., P_n$，一个包含 $m+1$ 个节点的节点向量 $U = { u_0, u_1, ..., u_m }$ 和次数 p，我们希望在不改变 B-样条 曲线 $C(u)$ 的形状的情况下，将一个新的节点$ t$ 插入到节点向量中。

假设新的节点$ t$ 位于节点区间 $[u_k, u_{k+1})$ 中。根据强凸包性质，$C(t)$ 位于由控制点 $P_k, P_{k-1}, ..., P_{k-p}$ 定义的凸包中，所有其他控制点的基函数都为零。因此，节点插入计算可以限制在控制点 $P_k, P_{k-1}, ..., P_{k-p}$ 上。

插入 $t$ 的方式是在边 $P_{k-1}P_k$ 上找到 $p$ 个新的控制点 $Q_k$，在边 $P_{k-2}P_{k-1}$ 上找到控制点 $Q_{k-1}$，…，在边 $P_{k-p}P_{k-p+1}$ 上找到控制点 $Q_{k-p+1}$。通过在 $P_{k-p+1}, ..., P_{k-1}$ 处切割角，可以使得在 $P_{k-p}$ 和 $P_k$ 之间的旧控制折线（如下图的黑色部分）被 $P_{k-p}Q_{k-p+1}...Q_kP_k$（如下图的黄色部分）替代，所有其他的控制点都没有改变。注意，原始控制折线的 $p-1 $个控制点被移除并被$ p$ 个新的控制点替换。

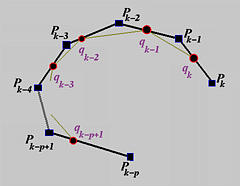
新控制点 $Q_i$ 的位置很容易计算。计算边 $P_{i-1}P_i$ 上的新控制点 $Q_i$ 的公式如下：

$$\mathbf{Q}_i=(1-a_i)\mathbf{P}_{i-1}+a_i\mathbf{P}_i$$

其中，比率 $a_i$ 的计算如下：

$$a_i=\frac{t-u_i}{u_{i+p}-u_i}\quad\text{for}\quad k-p+1\leq i\leq k$$

总的来说，要插入一个新的节点 $t$，我们首先找到包含 $t$ 的节点区间 $[u_k, u_{k+1})$。有了$ k$，我们可以用上面的公式计算出 $p$ 个新的控制点 $Q_{k-p+1}, ..., Q_k$。最后，将 $P_{k-p}$ 和 $P_k$ 之间的原始控制折线替换为由 $P_{k-p}, Q_{k-p+1}, Q_{k-p+2}, ..., Q_{k-1}, Q_k$ 和 $P_k$ 定义的新控制折线。注意，插入新节点后，节点向量变为 $u_0, u_1, ..., u_k, t, u_{k+1}, ..., u_m$。如果新的节点 t 等于 $u_k$，那么 $u_k$ 的重复度增加一。

上述计算过程可以用以下图来说明。首先，受影响的控制点列在左列。然后，计算出的新控制点列在第二列。注意，新控制点的数量比受影响的控制点少一个。新控制点 $Q_i$ 的计算，需要两个原始控制点 $P_{i-1}$ 和 $P_i$，系数分别为 $1-a_i$ 和 $a_i$。计算后，蓝色虚线圈起来的点为新的控制点，所有不受影响的控制点仍然保持不变。即，原始控制点集 $P_{k-p}, P_{k-p+1}, ..., P_{k-1}, P_k$ 被 $P_{k-p}, Q_{k-p+1}, ..., Q_{k-1}, P_k$ 替换。

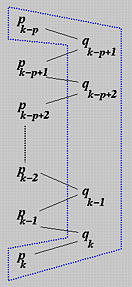
关于 $a_i$ 的几何解释，从其定义来看，$a_i : 1-a_i$ 是将区间 $[u_i, u_{i+p})$ 通过 $t$ 的值划分的比例，如下所示：

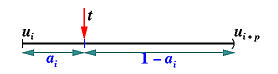
我们有 $k$ 个 $a_i$值，每个都覆盖 $p$ 个节点区间（即 $[u_i, u_{i+p})$）。如果我们将这些区间堆叠在一起，并在 $t$ 的值处对齐：

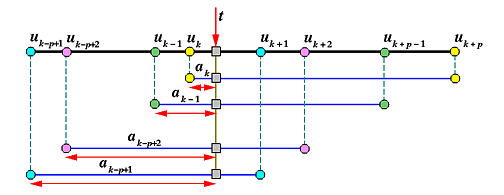
因此，$t$ 的位置将节点区间 $[u_k, u_{k+p})$，$[u_{k-1}, u_{k+p-1})$，…，$[u_{k-p+1}, u_{k+1})$ 划分为比例 $a_k$，$a_{k-1}$，…，$a_{k-p+1}$，同样的，这也是划分边 $P_kP_{k-1}$，$P_{k-1}P_{k-2}$，… $P_{k-p}P_{k-p+1}$ 的比例。

示例1：在节点区间中插入节点

假设我们有一个次数为3的B样条曲线，节点向量如下：

我们想要插入一个新的节点 $t = 0.5$。由于 $t = 0.5$ 位于节点区间 $[u_5,u_6)$ 中，所以受影响的控制点是 $P_5, P_4, P_3$ 和 $P_2$。为了确定三个新的控制点 $Q_5, Q_4$ 和 $Q_3$，我们需要计算 $a_5, a_4$ 和 $a_3$，如下所示：

$$a_{5}=\frac{t-u_{5}}{u_{8}-u_{5}}=\frac{0.5-0.4}{1-0.4}=\frac{1}{6}\\a_{4}=\frac{t-u_{4}}{u_{7}-u_{4}}=\frac{0.5-0.2}{0.8-0.2}=\frac{1}{2}\\a_{3}=\frac{t-u_{3}}{u_{6}-u_{3}}=\frac{0.5-0}{0.6-0}=\frac{5}{6}$$

三个新的控制点是

$$\begin{array}{rcl}\mathbf{Q}_5&=&\left(1-\frac{1}{6}\mathbf{P}_4\right)+\frac{1}{6}\mathbf{P}_5\\\mathbf{Q}_4&=&\left(1-\frac{1}{2}\mathbf{P}_3\right)+\frac{1}{2}\mathbf{P}_4\\\mathbf{Q}_3&=&\left(1-\frac{5}{6}\mathbf{P}_2\right)+\frac{5}{6}\mathbf{P}_3\end{array}$$

新的控制折线变为 $P_0, P_1, P_2, Q_3, Q_4, Q_5, P_5, ....$，新的节点向量是

由于原始的B样条曲线的 $p = 3$ 和 $m = 11$，我们有 $n = m - p - 1 = 11 - 3 - 1 = 7$，因此有8个控制点。下面是满足这个条件的B样条曲线和它的基函数：

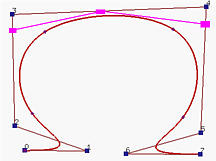
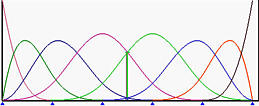
三个粉色的矩形是 $Q_3, Q_4$ 和 $Q_5$。插入 $t = 0.5$ 后，切掉了 $P_3$ 和 $P_4$ 的角，得到了以下的B样条曲线和它的基函数。注意，曲线的形状没有改变：

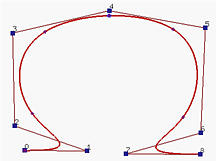
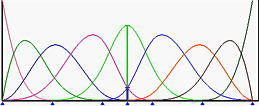
下图显示了旧的和新的控制点之间的关系，新的控制点集为$P_0, P_1, P_2, Q_3, Q_4, Q_5, P_5, P_6$ 和 $P_7$。

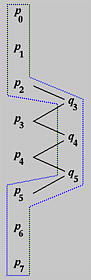
下面显示了 $a_j$，$u_j$ 和 $t$ 之间的关系：

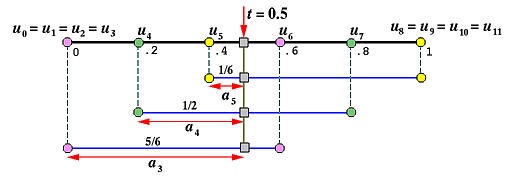
示例2：在现有的简单节点（重数为1）处插入节点，使其变为重复节点

假设我们有一个节点向量如下：

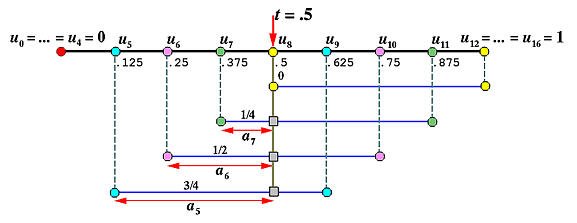
我们想要插入一个新的节点 $t = 0.5$，它等于一个现有的节点（即，$t = u_8 = 0.5$）。以下是在插入新节点之前的4次B样条曲线及其基函数。

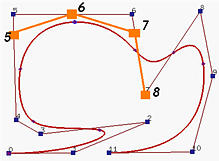
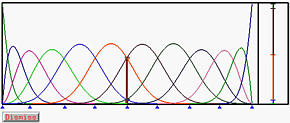
由于$ t$ 在 $[u_8,u_9)$ 中，所受影响的控制点是 $P_8, P_7, P_6, P_5$ 和 $P_4$。系数计算如下：

$$a_{8}=\frac{t-u_{8}}{u_{12}-u_{8}}=\frac{0.5-0.5}{1-0.875}=0$$

$$a_{7}=\frac{t-u_{7}}{u_{11}-u_{7}}=\frac{0.5-0.375}{0.875-0.375}=\frac{1}{4}$$

$$a_{6}=\frac{t-u_{6}}{u_{10}-u_{6}}=\frac{0.5-0.25}{0.75-0.25}=\frac{1}{2}$$

$$a_{5}=\frac{t-u_{5}}{u_{9}-u_{5}}=\frac{0.5-0.125}{0.625-0.125}=\frac{3}{4}$$

新的控制点是：

$$\\\mathbf{Q}_{8}=(1-0\mathbf{P}_{7})+0\mathbf{P}_{8}\\\mathbf{Q}_{7}=\left(1-\frac{1}{4}\mathbf{P}_{6}\right)+\frac{1}{4}\mathbf{P}_{7}\\\mathbf{Q}_{6}=\left(1-\frac{1}{2}\mathbf{P}_{5}\right)+\frac{1}{2}\mathbf{P}_{6}\\\mathbf{Q}_{5}=\left(1-\frac{3}{4}\mathbf{P}_{4}\right)+\frac{3}{4}\mathbf{P}_{5}$$

新的控制点 $Q_8$ 等于原始控制点 $P_7$。实际上，如果$ t$ 为现有的节点，比如 $u_k$，那么

$$a_k=\frac{t-u_k}{u_{k+p}-u_k}=0$$

因此，我们有

$$\mathbf{Q}_k=(1-0)\mathbf{P}_{k-1}+0\mathbf{P}_k=\mathbf{P}_{k-1}$$

也就是说，如果要插入的新节点 $t$ 等于一个现有的简单节点 $u_k$，那么 $Q_k$，最后一个新的控制点，等于 $P_{k-1}$。下图显示了计算过程：

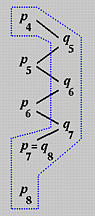
下图显示了新的控制点（橙色矩形）和新控制折线（橙色），注意新的控制点是 $P_0, P_1, P_2, P_3, P_4, Q_5, Q_6, Q_7, Q_8 = P_7, P_8, P_9, P_{10}$ 和 $P_{11}$。

插入新节点 $t = 0.5$ 后的曲线及其基函数如下所示。

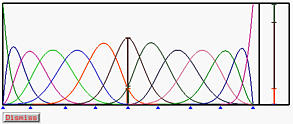
下面显示了 $a_j$，$u_j$ 和 $t$ 之间的关系：

示例3：在现有的多重节点处插入节点

假设 $t$ 插入在重复度为 $s$ 的节点 $u_k$ 处。我们有 $s$ 个连续相等的节点：$u_k = u_{k-1} = u_{k-2} = .... = u_{k-s+1}$ 并且 $u_{k-s+1}$ 不等于 $u_{k-s}$。在计算系数 $a_k, ...., a_{k-p+1}$ 时，我们有以下情况：

$$a_{k}=\frac{t-u_k}{u_{k+p}-u_k}=\frac{u_k-u_k}{u_{k+p}-u_k}=0$$

$$a_{k-1}=\frac{t-u_{k-1}}{u_{k+p-1}-u_{k-1}}=\frac{u_k-u_{k-1}}{u_{k+p-1}-u_{k-1}}=0$$

$$a_{k-s+1}=\frac{t-u_{k-s+1}}{u_{k-s+1+p}-u_{k-s+1}}=\frac{u_k-u_{k-s+1}}{u_{k-s+1+p}-u_{k-s+1}}=0$$

因此，系数 $a_k, ...., a_{k-p+1}$ 都是零，因此，我们有

$$\mathbf{Q}_{k}=(1-a_k)\mathbf{P}_{k-1}+a_k\mathbf{P}_k=\mathbf{P}_{k-1}$$

$$\mathbf{Q}_{k-1}=(1-a_{k-1})\mathbf{P}_{k-2}+a_{k-1}\mathbf{P}_{k-1}=\mathbf{P}_{k-2}$$

$$\mathbf{Q}_{k-s}=(1-a_{k-s+1})\mathbf{P}_{k-s}+a_{k-s+1}\mathbf{P}_{k-s}=\mathbf{P}_{k-s}$$

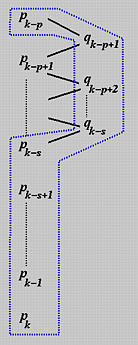
这表明，如果新的节点 $t$ 插入在重复度为 $s$ 的节点 $u_k$ 处，那么最后 $s$ 个新的控制点 $Q_k, Q_{k-1}, ..., Q_{k-s+1}$ 等于原始控制点 $P_{k-1}, P_{k-2}, ..., P_{k-s}$。如果 $s = 1$（即，简单节点），$Q_k$ 等于 $P_{k-1}$，这正是示例2中讨论的。如果 $s = 0$（即，t 不是一个节点），那么所有从 $P_{k-p}$ 到 $P_k$ 的控制点都参与其中。这是示例1的情况。下图显示了计算过程：

B样条曲线多次插入节点

在许多应用中，需要多次插入节点。一个方法是反复应用单个节点插入算法，然而这种方式，原始的节点向量和原始的控制点集必须在每次插入后进行修改，这是一个相当繁琐的任务。我们可以找到一个更简单的方法来实现这个效果。

观察一：计算新控制点的系数

先从简单的情况开始。假设$t$要插入在节点区间 $[u_k, u_{k+1})$ 的中间，曲线次为$p$。第一次插入的系数 $a_{i,1}$，其中 $k-p+1 \leq i \leq k$，计算如下：

$$a_{i,1}=\frac{t-u_i}{u_{i+p}-u_i}$$

插入 $t$ 后，得到一个新的节点，节点 $u_{k+1}, u_{k+2}, ..., u_m$ 将向右移动一个位置。更准确地说，新的节点为 $v_0, v_1, ..., v_k, v_{k+1}, ..., v_m$ 和 $v_{m+1}$ ，如下：

$v_{k+1}$ 将新的节点向量一分为二，$v_{k+1} = t$ 左边的节点与原始值相同，而 $t$ 右边的节点满足关系 $v_h = u_{h-1}$，（即新的节点值等于原始节点向量中对应的前一个位置的节点值）
如果 $t$ 再次被插入，它位于节点区间 $[v_{k+1},v_{k+2})$ 中。由于$t = v_{k+1}$，这次插入使得 $v_{k+1}$ 成为一个双重节点。这次插入的系数 $a_{i,2}$，基于新的节点序列，计算如下：

$$a_{i,2}=\frac{t-v_i}{v_{i+p}-v_i}$$

其中 $k-p+1 \leq i \leq k+1$。用$u$ 代替节点$v$表示，得到：

$$a_{i,2}=\frac{t-u_i}{u_{i+p-1}-u_i}$$

注意，$u_i$ 在 $t = v_{k+1}$ 的左边，$u_{i+p}$ 在 $v = v_{k+1}$ 的右边。

设新的节点向量是 $w_i$。这个新节点向量和原节点向量的关系如下所示：

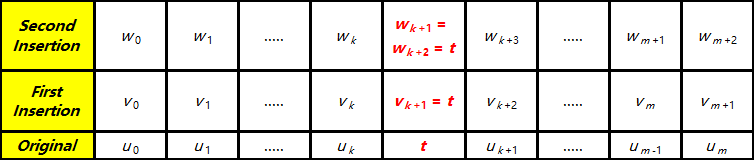
继续插入 $t$ ，使得 $w_{k+1}$ 成为一个三重节点，第三次插入的系数 $a_{i,3}$ 为：

$$a_{i,3}=\frac{t-w_{i}}{w_{i+p}-w_{i}}$$

上述公式可以重写为：

$$a_{i,3}=\frac{t-u_i}{u_{i+p-2}-u_i}$$

依此类推，可以得到第$h$次插入节点$t$时，系数$a_{i,h}$的计算公式为：

$$a_{i,h}=\frac{t-u_i}{u_{i+p-(h-1)}-u_i}$$

如果在初始的节点向量中，$u_k$ 是一个重复度为 $s$ 的多重节点，并且 $t$ 被插入在 $u_k$ 处，这也不会影响上述公式。因为，如果 $u_k$ 是一个重复度为 $s$ 的多重节点，那么

$u_k = u_{k-1} = u_{k-2} = ... = u_{k-s+1}$:

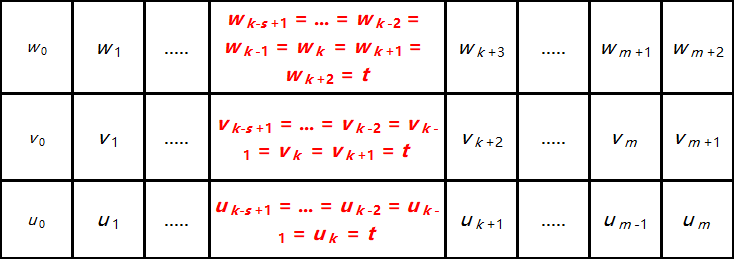
上述节点都位于 $t$ 的左侧，并且节点的移动只发生在 $t$ 的右侧的结点，所以 $a_{i,h}$ 的计算公式不需要修改。因此，我们有结论：

如果一个新的节点 $t$ 被插入到[$u_k$, $u_{k+1}$) 区间 $h$ 次，那么系数 $a_{i,h}$ 可以按照以下方式计算：

$$a_{i,h}=\frac{t-u_i}{u_{i+p-(h-1)}-u_i}$$

观察二：新控制点的计算

如果在重复度为$s$的现有节点$u_k$处插入$t$，则控制点 $P_{k-s}, P_{k-s+1}, ..., P_{k-1}$ 和 $P_k$ 不受影响，只有 $P_{k-p}, P_{k-p+1}, ..., P_{k-s}$ 参与新控制点 $Q_i$ 的计算。我们用第二个下标1表示第一次插入后的所有新控制点。因此，我们有下图：

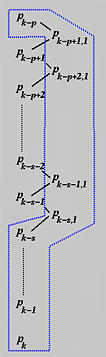
如果同一个节点被插入第二次，受影响的 $p+1$ 个控制点是 $P_k, P_{k-1}, P_{k-s}, P_{k-s,1}, P_{k-s-1,1}, ..., P_{k-p+1,1}$，如上图所示。

注意，$P_{k-p}$ 被排除在外，因为只有 $p+1$ 个控制点受影响。然而，由于前一次插入使得 $t$的重复度增加了一，所以不参与节点插入计算的控制点数量为 $s+2$，即$P_k, P_{k-1}, ..., P_{k-s}$ 和 $P_{k-s,1}$。

计算过程和新的控制点集如下图所示。从第二次插入生成的新控制点的第二个下标为2。新的控制点由两部分组成：（1）从第一次插入计算出的 $P_{k-p+1,1}$ 和 $P_{k-s,1}$，以及（2）从第二次插入计算出的 $P_{k-p+2,2}$ 到 $P_{k-s,2}$。

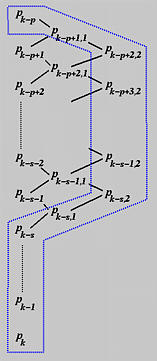
对于第三次插入，受影响的 $p+1$ 个控制点是 $P_{k-p+2,2}$ 到 $P_{k-s,2}$，$P_{k-s,1}$，以及 $P_{k-s}$ 到 $P_k$。由于这第三次插入再次增加了$t$的重复度，不参与计算的控制点数量也增加了一。因此，$P_{k-s,2}$ 在第三次插入前后将保持不变。下图表示了这个过程：

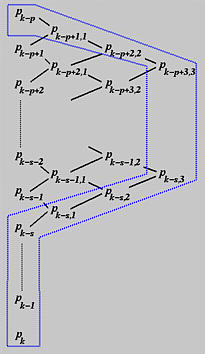
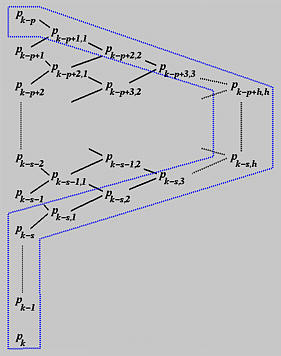
一般来说，如果在重复度为$s$的节点$u_k$处插入节点$t$ $h$次，其中$s = 0$表示t被插入到该节点区间的中间，$s > 0$表示$t$被插入到重复度为$s$的节点$u_k$，我们可以通过以下方式计算新的控制点列：
1.写下第一组受影响的 $p+1$ 个控制点作为第0列；
2.忽略最后的$s$个控制点（即，$P_{k-s+1}$ 到 $P_k$）；
3.计算第一列，第二列，… 和第$h$列；
4.新的控制点集是被蓝色多边形围绕的那些

小结

通过上面几个观察，我们有以下多次插入节点$t$的算法：

输入：将节点 $t$ 插入 [$u_k$ ，$u_{k+1}$)，初始重数为 $s$，插入 $h$ 次，其中 $h+s$ 小于或等于所给 B-样条曲线的阶数 $p$
输出：在 $t$ 被插入 $h$ 次后的新的控制点集合

让控制点 $P_k, P_{k-1}, ..., P_{k-p}$ 通过添加第二个下标0重命名为 $P_{k,0}, P_{k-1,0}, ..., P_{k-p,0}$。

for $r$= 1 to $h$ do
for $i$ = $k-p+r$ to $k-s$ do
begin
Let $a_{i,r}$ = ($t$ - $u_i$) / ( $u_{i+p-r+1}$ - $u_i$ )
Let $P_{i,r}$ = (1 - $a_{i,r}$) $P_{i-1,r-1}$ + $a_{i,r}P_{i,r-1}$
end

新的控制点组是由从原始的 $P_0$ 到 $P_{k-p}$ 的点构造而成，然后是上图边缘（即 $P_{k-p+1,1}$, $P_{k-p+2,2}$, …, $P_{k-p+h,h}$），接着是图的右边缘（即 $P_{k-p+h+1,h}$, $P_{k-p+h+2,h}$, …, $P_{k-s,h}$），然后是图的底边缘（即 $P_{k-s,h-1}$, $P_{k-s,h-2}$, …, $P_{k-s,1}$），最后是原始的控制点 $P_{k-s}$，…，$P_k$，…，$P_n$。

角切割

如前所述，节点插入是一个角切割过程。例如，假设我们有一个6次的B样条曲线，想在重复度为2的节点$u_10$处插入$u$两次。受影响的控制点是 $P_{10}, P_{9}, ..., P_{4}$，因为$k = 10$，$p = 6$且$k-p = 4$。由于$u_10$的重复度是2，我们有$s = 2$且$u_{10}$和 $P_9$ 不变。第一次插入产生 新的控制点$P_{8,1}, P_{7,1}, P_{6,1}$ 和 $P_{5,1}$，相当于在 $P_7, P_6$ 和 $P_5$ 处切割角。新的控制点集为 $P_0$ 到 $P_4, P_{5,1}, P_{6,1}, P_{7,1}, P_{8,1}, P_8, P_9, P_{10}, .....$

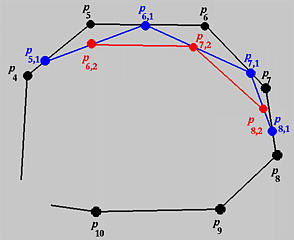
第二次插入产生 $P_{8,2}, P_{7,2}$ 和 $P_{6,2}$。因此，相当于在 $P_{7,1}$ 和 $P_{6,1}$ 处切割角，新的控制点集为 $P_0$ 到 $P_4, P_{5,1}, P_{6,2}, P_{7,2}, P_{8,2}, P_{8,1}, P_8, P_9, P_{10}, .....$

$de Boor$ 算法

$de Boor$的算法是$de Casteljau$算法的推广。它提供了一种快速且数值稳定的方法，用于计算给定 $u$ 值时，B样条曲线上的点$C(u)$。

回想一下多重节点的一个性质，增加节点的重数会减少在此节点处非零基函数的数量。

如果这个节点的重数是 $k$，那么在这个节点处最多有 $p - k + 1$ 个非零基函数。因此，在重数为 $p$ 的节点处，只会有一个非零基函数，并根据B样条基函数的单位分解性质，我们知道该非零基函数的值为1。

假设这个节点为 $u_i$。如果 $u$ 的取值为 $u_i$，由于 $N_{i,p}(u)$ 在 $[u_i,u_{i+1})$ 上非零，曲线 $C(u)$ 上的点受到恰好一个控制点 $P_i$ 的影响。因此我们有：

$$C(u) = N_{i,p}(u) P_i = P_i$$

那么，这个有趣或有些奇怪的性质的意义是什么呢？

简单来说：如果一个节点 $u$ 被反复插入，使得其重数为 $p$，那么最后生成的新控制点就是对应于 $u$ 值处曲线上的点。

为什么会这样呢？在多次插入 $u$ 后，使其重数为 $p$，三角计算方案产生一个点。因为给定的B样条曲线必须经过这个新点，所以它是对应于 $u$ 的曲线上的点。

这个观察为我们提供了一种在曲线上找到任意一点 $C(u)$ 的方法！我们只需插入 $u$，直到其重数变为 $p$，最后一个点就是 $C(u)$

让我们看一个例子

图(a)是由7个控制点定义的4次B样条曲线，下面要计算 $C(0.9)$，$u=0.9$不是一个节点，将$u = 0.9$ 连续插入4次。

图(b)和图©显示了第一次和第二次插入后的结果，在右下角附近添加了两个新的控制点，新的控制折线比原来的控制折线更接近曲线。第三次插入的结果显示在图(d)中。第四次插入后，产生的控制点位于曲线上，见图(e)。因此，在四次插入后， $C(0.9)$ 是一个控制点。

（a)	（b)	（c)
（d)	（e)

在前面讨论的一般节点插入算法可以满足我们的需求。

注意，我们只需要插入足够多次数的 $u$，使得 $u$ 成为一个重数为 $p$ 的节点。如果 $u$ 已经是一个重数为 $s$ 的节点，那么插入它 $p - s$ 次就足够了。

输入：一个值$u$
输出：曲线上的点$C(u)$
如果$u$位于$[u_k，u_{k+1})$并且$u \neq u_k$，让$h = p$（即插入$u$ $p$次）和$s = 0$；如果$u = u_k$且$u_k$是重数为$s$的结点，则让$h = p - s$（即插入$u$ $p - s$次）；复制受影响的控制点$P_{k-s}$，$P_{k-s-1}$，$P_{k-s-2}$，…，$P_{k-p+1}$和$P_{k-p}$到一个新数组，并将它们重命名为$P_{k-s,0}$，$P_{k-s-1,0}$，$P_{k-s-2,0}$，…，$P_{k-p+1,0}$。

for $r$= $1$ to $h$ do
for $i$ = $k-p+r$ to $k-s$ do
begin
Let $a_{i,r} = (u - u_i) / ( u_{i+p-r+1} - u_i )$
Let $P_{i,r}= (1 - a_{i,r}) P_{i-1,r-1} + a_{i,r} P_{i,r-1}$
end
$P_{k-s,p-s}$ is the point $C(u)$.

在下面的图中，所有的 $P_{i,0}$ 都在左列。根据第$0$列和系数 $a_{i,1}$，可以计算出 $P_{i,1}$。
然后根据第一列结果和系数 $a_{i,2}$，可以计算出第二列，依此类推。

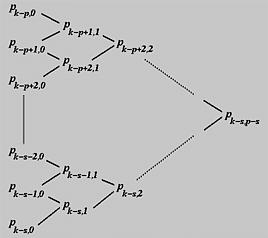
由于在第$0$列上有 $p-s+1$ 个点，而且每一列的点数都比前一列少一个，所以需要 $p-s$ 列来将一列上的点数减少到1。这就是为什么最后一个点是 $P_{k-s,p-s}$。下面的图显示了角切割的过程。

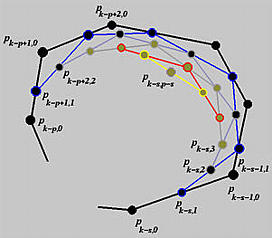
尽管这个过程看起来像是从$de Casteljau$的算法中得到的，但它们却截然不同。

首先，在$de Casteljau$的算法下，划分点是用一对数字 $1 - u$ 和 $u$ 计算的，这两个数字在整个计算过程中都不会改变，而在$de Boor$的算法下，这些数字对是不同的，取决于列号和控制点。

其次，在$de Boor$的算法中，只有 $p+1$ 个受影响的控制点参与计算，而$de Casteljau$的算法使用所有的控制点。由于控制点 $P_{k-p}$ 到 $P_k$ 在节点区间 $[u_k, u_{k+1})$ 上定义了一个包含曲线段的凸包，所以$de Boor$的算法的计算是在相应的凸包内进行的。

一个例子

假设我们有一个由7个控制点 $P_0, ..., P_6$（即，$n = 6$）定义的3阶（即，$p = 3$）B样条曲线，以及以下11个节点（即，$m = 10$）的节点向量：

我们将计算 $P(0.4)$。对于de Boor的算法，这相当于插入 $u = 0.4$ 三次。由于 $u = 0.4$ 不是现有的节点，即$s = 0$ 且 $u = 0.4$ 在 $[u_4, u_5)$ 中，受影响的控制点是 $P_4, P_3, P_2$ 和 $P_1$。下图展示了这个计算过程：

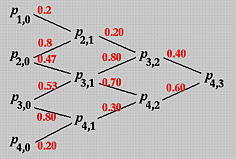
首先计算第一列。涉及的系数是

$$a_{4,1}=\frac{u-u_4}{u_{4+3}-u_4}=0.2$$

$$a_{3,1}=\frac{u-u_3}{u_{3+3}-u_3}=8/15=0.53$$

$$a_{2,1}=\frac{u-u_2}{u_{2+3}-u_2}=0.8$$

第一列的计算如下：

$$\mathbf{P}_{4,1}=(1-a_{4,1})\mathbf{P}_{3,0}+a_{4,1}\mathbf{P}_{4,0}=0.8\mathbf{P}_{3,0}+0.2\mathbf{P}_{4,0}\\\mathbf{P}_{3,1}=(1-a_{3,1})\mathbf{P}_{2,0}+a_{3,1}\mathbf{P}_{3,0}=0.47\mathbf{P}_{2,0}+0.53\mathbf{P}_{3,0}\\\mathbf{P}_{2,1}=(1-a_{2,1})\mathbf{P}_{1,0}+a_{2,1}\mathbf{P}_{2,0}=0.2\mathbf{P}_{1,0}+0.8\mathbf{P}_{2,0}$$

要计算第二列，我们需要以下系数：

$$a_{4,2}=\frac{u-u_4}{u_{4+3-1}-u_4}=0.3$$

$$a_{3,2}=\frac{u-u_3}{u_{3+3-1}-u_3}=0.8$$

对应的点是

$$\mathbf{P}_{4,2}=(1-a_{4,2})\mathbf{P}_{3,1}+a_{4,2}\mathbf{P}_{4,1}=0.7\mathbf{P}_{3,1}+0.3\mathbf{P}_{4,1}\\\mathbf{P}_{3,2}=(1-a_{3,2})\mathbf{P}_{2,1}+a_{3,2}\mathbf{P}_{3,1}=0.2\mathbf{P}_{2,1}+0.8\mathbf{P}_{3,1}$$

最后一列：

$$a_{4,3}=\frac{u-u_4}{u_{4+3-2}-u_4}=0.6$$

所以最后的点是

$$\mathbf{P}_{4,3}=(1-a_{4,3})\mathbf{P}_{3,2}+a_{4,3}\mathbf{P}_{4,2}=0.4\mathbf{P}_{3,2}+0.6\mathbf{P}_{4,2}$$

这是对应于 $u = 0.4$ 处曲线上的点。

请注意，de Boor算法生成的中间的控制折线与de Casteljau算法生成的控制折线非常相似。在这个例子中，$u$不是一个节点。如果$u$是一个节点，计算会更容易，因为受影响的控制点数量会更少。

de Boor算法 vs de Casteljau算法

因为贝塞尔曲线是特殊形式的B样条曲线，而$de Boor$算法与$de Casteljau$算法非常相似，我们希望后者是前者的一种特殊情况，事实发现，的确如此。

假设我们有一个由 $n+1$ 个控制点 $P_0, ..., P_n$ 定义的 $n$ 次B样条曲线 $C(u)$，并且前$p+1$个节点值为$0$，紧跟着是$p+1$个值为$1$的节点，这种情况下，$C(u)$ 实际上是一个 $n$ 阶的Bézier曲线。（见前面"B样条曲线：特殊情况" 章节）

根据$de Boor$算法的计算步骤。我们已知 $C(0) = P_0$ 和 $C(1) = P_n$。我们需要证明的是，对于每一个 $u$，$de Boor$的算法和$de Casteljau$的算法的计算过程相同，并且得到相同的结果。

设节点为 $u_0 = u_1 = ... = u_n = 0$ 和 $u_{n+1} = u_{n+2} = ... = u_{2n+1} = 1$。对于任意给定 $u$值，它在 $[u_n, u_{n+1})$ 中。因此，参与节点插入计算的控制点是 $P_n, ..., P_{n-n} = P_0$，用于计算 $a_i$ 的区间是 $[u_n, u_{n+n}) = [0,1)$，$[u_{n-1}, u_{n+n-1}) = [0,1)$，…，和 $[u_{n-n+1}, u_{n+1}) = [0,1)$。因此，对于每一个 $i$，我们有

$$a_i=\frac{u-u_i}{u_{i+n}-u_n}=u\quad\text{for}1\leq i\leq n$$

由于每一条边都以 $a_i:1-a_i$ 的比例划分，在这个特殊情况下，划分比例都是相同的，等于 $u:1-u$。因此，通过$de Boor$算法计算出的第一次节点插入的结果，恰好是$de Casteljau$算法中计算结果的第一列。

同理，所有后续插入步骤中的划分比例也等于 $u:1-u$。因此，在这个特殊情况下，$de Boor$算法的计算过程与$de Casteljau$算法的相应步骤完全相同。

因此，当节点向量只有两个重数为 $n+1$ 的节点时，$de Boor$的算法就简化为$de Casteljau$的算法。

B样条曲线的细分

B样条曲线细分的过程与$Bézier$曲线细分的过程完全相同。但是，我们将使用$de Boor$的算法对B样条曲线进行细分。

选择控制点

假设我们想在 $u$ 处将一个B样条曲线细分为两个B样条曲线，一个在$[0,u]$上，另一个在$[u,1]$上。

首先要做的是在$u$处应用$de Boor$的算法。注意，如果$u$在$[u_k, u_{k+1})$中，那么在计算中最多会使用$p+1$个控制点，即：$P_k, P_{k-1}, ..., P_{k-p}$

为了找到在区间$[0,u]$上的B样条曲线的控制点，我们从$P_0$开始并沿着控制折线寻找，当我们遇到一个控制点或在$de Boor$算法过程中计算出的点时，我们选择那个点并转弯。这个过程一直持续到我们到达$C(u)$，该点也被选为控制点。这些点，按访问连接，形成了定义$[0,u]$上的B样条曲线的控制点。

对于定义在$[u,1]$上的B样条曲线，我们从点$C(u)$开始，每遇到一个点就选择该点并转弯，直到到达$P_n$ 。这个顺序很重要！！！

例子

下面显示了由11个（$n = 10$）控制点定义的3次B样条曲线。假设我们希望在$u = 0.5$处细分这条曲线。使用$de Boor$算法计算$C(0.5)$的过程生成了一个$de Boor$包络网。

在下图中，第0列上的点用圆圈标记，第1列上的点用方形标记，第2列上的点用三角形标记，第3列上的点用五边形标记，曲线$C(u)$上的点在第4列。

因此，$[0,u]$上的B样条曲线的控制点是$P_0, P_1, P_2, P_3, P_4, a$（转弯），$b$（转弯），$c$（转弯），和$C(0.5)$ ,定义在$[u,1]$上的B样条曲线的控制点是$C(0.5), d$（转弯），$e$（转弯），$f$（转弯），$P_8, P_9$和$P_{10}$。

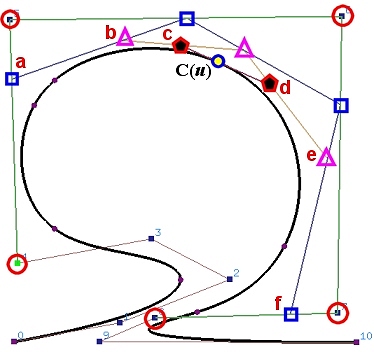
因此，$[0,u]$上曲线的控制点包括原始的未受影响的控制点和$de Boor$包络网的每条折线的第一个点。同样，$[u,1]$上的曲线的控制点由$de Boor$包络网的每条折线的最后一个点组成，然后是其他未受影响的控制点。

由于$de Boor$包络网的控制折线的第一个点和最后一个点是同一列的第一个点和最后一个点，所以一旦该列完全计算出来，就可以得到对应的值。

在下面显示$de Boor$算法的三角形计算方案的图中，我们可以立即提取$P_{k-p}$（$[0,u]$上的曲线）和$P_{k-s}$（$[u,1]$上的曲线）。一旦计算出第1列，我们可以提取$P_{k-p+1,1}$（$[0,u]$上的曲线）和$P_{k-s,1}$（$[u,1]$上的曲线）。计算出第2列后，我们可以提取$P_{k-p+2,2}$（$[0,u]$上的曲线）和$P_{k-s,2}$（$[u,1]$上的曲线）。这个过程一直持续到我们到达$P_{k-s,p-s} = C(u)$，它将被选为两条曲线的控制点。

因此，从图形上看，从$P_0$到$P_{k-s,p-s}$的楔形的上边缘上的点形成了$[0,u]$上的曲线的控制点，从$P_{k-s,p-s}$到$P_n$的下边缘上的点形成了$[u,0]$上的曲线的控制点。

选择节点

曲线在$[0,u]$上的节点向量包括$[0,u)$中的所有节点，加上$p+1$个重复的$u$值，而曲线在$[u,1]$上的节点向量包括$p+1$个重复的$u$值，和$(u,1]$中的所有节点。

例如，如果一个B样条曲线的次数为4，其原始节点向量为${ 0(5), 0.3, 0.4, 0.6, 0.7, 0.85, 0.9, 1(5) }$. 如果曲线在$u = 0.65$处被划分，那么$[0,0.65]$上曲线的节点向量为 ${ 0(5), 0.3, 0.4, 0.6, 0.65(5) }$，而$[0.65, 1]$上曲线的节点向量为 ${ 0.65(5), 0.7, 0.85, 0.9, 1(5) }$。

可以证明，这样构造的组合曲线也是和原始B样条曲线具有相同的次数，并且在$[0,u]$段和$[u,1]$段，属于原曲线的一部分。

将B样条曲线细分为贝塞尔曲线段

如果一个次数为$p$的B样条曲线在其节点处被细分，那么每个曲线段都会变成一个$p$次的贝塞尔曲线。下图显示了一个例子。

图(a)是由7个（$n = 6$）控制点和节点向量${ 0(5), 1/3, 2/3, 1(5) }$定义的4次B样条曲线。
图(b)显示了$u = 1/3$时的$de Boor$包络网
图©显示了细分完成后选定的控制点
现在，$[0,1/3]$上的曲线段是一个3次贝塞尔曲线，而第二个曲线段$[2/3,1]$仍然是由6个（$n = 5$）控制点和一个节点向量${ 1/3(5), 2/3, 1(5) }$定义的4次B样条曲线。
图(d)显示了$u = 2/3$处的$de Boor$包络网
图(e)显示了细分的曲线，一个在$[1/3,2/3]$，另一个在$[2/3,1]$.
图(f)显示了原始控制折线和三个贝塞尔段的控制折线。原始的B样条曲线有7个控制点。然而，三个贝塞尔曲线的控制点总数是13，几乎翻了一倍。

(a)	(b)	©
(d)	(e)	(f)

为什么每个曲线段都是一个贝塞尔曲线？

由于给定的B样条曲线在其节点处被细分，每个曲线段没有内部节点。此外，细分过程使得内部节点具有$p+1$的重复度，每个曲线段在曲线段的第一个和最后一个控制点处被$clamped$住。从前面的章节中，我们知道这些曲线段必须是贝塞尔曲线。

在细分B样条曲线的过程中，会引入大量的控制点。因此，操作B样条曲线比操作其组成的贝塞尔曲线更容易。此外，B样条曲线在节点对应的点处是$C^{p-k}$连续的，其中$k$是相应节点的重复度。当我们通过移动控制点来操作B样条曲线时，这种连续性总是被保持的。

然而，如果一个B样条曲线被细分成一系列的贝塞尔曲线，就很难保持在连接控制点处的连续性。因此，处理一个B样条曲线比处理一系列的贝塞尔曲线要容易得多。