解析曲线和曲面
下图展示了三种用平面切割圆锥的方式。从左到右,切割后的截面分别是椭圆、双曲线和抛物线。



曲线
圆
最简单的非线性曲线毫无疑问是圆。一个中心为(a,b),半径为r的圆方程如下:
(x−a)2+(x−b)2=r2
如果中心是原点,上述方程可简化为
x2+y2=r2
上述方程被称为圆的隐式形式。圆的参数形式为
x=rcos(t)
y=rsin(t)
如果圆心不在原点,则圆的参数形式为
x=a+rcos(t)
y=b+rsin(t)
上述参数形式使用三角函数。稍后我们将讨论一个不使用三角函数的圆的参数形式。
圆锥曲线
圆锥曲线是一个平面与一个圆锥体相交的曲线。
有三种非退化圆锥曲线:椭圆、双曲线和抛物线。椭圆和双曲线被称为中心圆锥曲线,因为它们有对称中心,而抛物线则是非中心对称的。
椭圆的隐式方程表示:
a2x2+b2y2=1
这个椭圆的轴是x轴和y轴,a和b是轴长,a和b中较大的是长轴,较小的是短轴。很容易看出,这种形式的椭圆具有以下参数形式:
x=acos(t)y=bsin(t)
双曲线的隐式方程表示:
a2x2−b2y2=1
主轴和次轴与椭圆的定义相同。x轴与曲线相交于两点(a,0)和(−a,0),而y轴则不与曲线相交。
双曲线的参数形式如下所示:
x=asec(t)y=btan(t)
在标准形式下,椭圆和双曲线的中心都位于坐标原点,并且它们是中心对称和轴对称的。
抛物线的隐式方程:
x2=4py
在这个标准形式中,对于抛物线上的任意点(x,y),y的值必须为正,并且这个抛物线向上开口。抛物线的标准形式已经是一个参数形式。或者,你可以将它重写为以下形式:
x=ty=4pt2
一般形式的圆锥曲线
圆锥曲线是二次曲线,因为它们的一般形式是下面的隐式二次多项式:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0
这个多项式有六个系数,如果将其除以非零系数,可以由六个未知数减少到五个。因此通常情况下,五个条件可以唯一确定一个圆锥曲线。
如何知道一个二次多项式的曲线类型?在这种情况下,只要二次方程表示的是一个圆锥曲线而不是两条相交或平行线,就可以通过以下方式判断:
- 如果 B2<A×C,方程表示一个椭圆。
- 如果 B2=A×C,方程表示一个抛物线。
- 如果 B2>A×C,方程表示一个双曲线。
表达式 B2−A×C 被称为一般二次多项式的 判别式。
圆锥曲线的一般形式也可以使用矩阵来表示。首先,将每个点 x=(x,y)视为第三分量为1的三维列向量,其转置向量为 xT=[x,y,1]。接下来,使用通用二次多项式的六个系数构造一个3×3对称矩阵,如下所示:
x=⎣⎢⎡xy1⎦⎥⎤xT=[x,y,1]Q=⎣⎢⎡ABDBCEDEF⎦⎥⎤
因此,一般形式的二次多项式可以改写成
xTQx=0
表面
一般形式的二次曲面
二次曲面,通常包括以下不同类型:椭球体、单叶双曲面、双叶双曲面、椭圆抛物面和双曲抛物面。以下是它们的隐式表示及形状:
a2x2+b2y2+c2z2=1
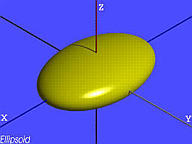
-
单叶双曲面(Hyperboloid of One Sheet):
a2x2+b2y2−c2z2=1
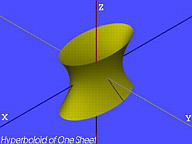
-
双叶双曲面(Hyperboloid of Two Sheets):
a2x2−b2y2−c2z2=1
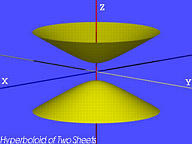
-
椭圆抛物面(Elliptic Paraboloid):
a2x2+b2y2=2cz
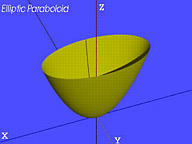
-
双曲抛物面(Hyperbolic Paraboloid):
a2x2−b2y2=2cz
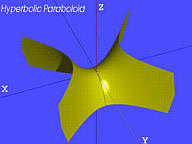
这五个二次曲面通常被称为四阶二次曲面。有两种类型的三阶二次曲面:圆锥和圆柱。圆柱有三个子类型:椭圆柱、双曲柱和抛物柱。如下所示:
-
圆锥(Cone):
a2x2+b2y2−c2z2=0
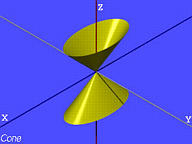
-
椭圆柱(Elliptic Cylinder):
a2x2+b2y2=1
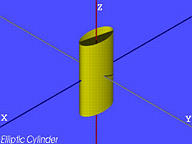
-
双曲圆柱体(Hyperbolic Cylinder):
a2x2−b2y2=1
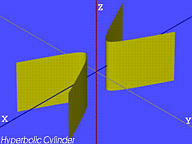
-
抛物线圆柱体(Parabolic Cylinder):
x2=4py
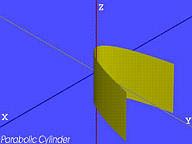
一般形式的二次曲面
二次曲面的一般形式如下:
Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+2Gx+2Hy+2Iz+J=0
它有十个系数;但是,将方程除以其中一个非零系数会将系数的数量减少到九个。
矩阵形式的二次曲面
一般二次曲面的方程也可以表示为矩阵形式:
x=⎣⎢⎢⎢⎡xyz1⎦⎥⎥⎥⎤xT=[x,y,z,1]Q=⎣⎢⎢⎢⎡ADEGDBFHEFCIGHIJ⎦⎥⎥⎥⎤
其中,(x,y,z) 是一个点的坐标。这个形式将一个二次曲面的一般二次多项式转换为以下矩阵形式:
xTQx=0
它与圆锥曲线的矩阵形式是相同的。
关于秩为4和秩为3的二次曲面的含义:
考虑二次多项式系数矩阵 Q。矩阵的秩是非零特征值的数量。因此,秩为4的二次曲面是指其系数矩阵 Q 的秩为4。
很容易从它们的标准形式中看出,
标准形式的环面
一个环面可以通过将一个圆(称为次圆),绕着一条线(旋转轴)旋转生成。
在旋转的过程中,次圆圆心的路径为另一个圆,称为主圆。主圆和次圆的半径分别称为主半径和次半径,分别表示为R和r。
如果旋转轴是 z 轴,主圆位于 xy 平面上,生成的环面的方程如下所示:
(x2+y2+z2−(R2+r2))2=4R2(r2−z2)

- 如果R>r,则生成的结果是一个常见的环面,如上图中间所示。
- 如果 R=r,那么所有移动圆都在坐标原点与旋转轴相切,如右图所示。
- 如果 R<r,则所有移动圆与旋转轴相交于两个不同的点,并且生成的环面将在环面内部呈现橄榄状,如左图所示。





















