NURBS(Non-Uniform Rational B-Splines) 是一种用于数学建模和计算机图形学的技术。它是一种灵活的用于描述曲线和曲面的方法,具有广泛的应用,包括计算机辅助设计(CAD)、计算机图形学、虚拟现实等领域。NURBS之所以受到青睐,是因为它们可以以高度灵活的方式控制曲线和曲面的形状,同时保持数学上的精确性。
NURBS通过基函数的组合来定义曲线和曲面,这些基函数是基于B样条(B-Splines)基函数的改进,但与B样条不同的是,NURBS允许在基函数中引入 权重 ,从而更灵活地控制曲线和曲面的形状。具体来说,NURBS曲线和曲面可以由控制点 、权重 以及次数 为基础的基函数来定义。这种灵活性使得NURBS能够更好地适应不同形状和设计需求。
B-样条曲线是多项式曲线 。虽然它们灵活且在曲线设计中具有许多良好的特性,但它们不能表示最简单的曲线:圆 。圆只能用有理函数 表示(即,两个多项式的商)。为了处理圆、椭圆和许多其他不能用多项式表示的曲线,因此需要对B样条曲线进行扩展。
圆是一个二次曲线。为什么B样条曲线不能表示它?
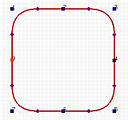
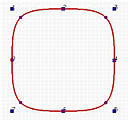
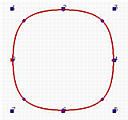
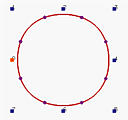
以下是四个闭合的B样条曲线,具有8个控制点。从左到右的度数分别是2、3、5和10。二次闭合的B样条看起来不像一个圆,它看起来像一个圆角正方形。三次曲线看起来稍微好一些。随着度数的增加,曲线的"圆润程度"变得更好。十次闭合曲线与圆非常相似;但它依旧不是一个圆。即使你可以把这个十次曲线作为一个圆接受,这也是近似的。
为了解决这个问题,我们将使用 “齐次坐标” 将B样条推广为 有理曲线 。因此,我们有了N on-U niform R ational B -S plines,即NURBS曲线 。
我们将齐次坐标 引入到B样条曲线中并推导NURBS 曲线的定义:
给定 n + 1 n+1 n + 1 P 0 , P 1 , . . . , P n P_0, P_1, ..., P_n P 0 , P 1 , . . . , P n m + 1 m+1 m + 1 U = u 0 , u 1 , . . . , u m U = { u_0, u_1, ..., u_m } U = u 0 , u 1 , . . . , u m p p p
C ( u ) = ∑ i = 0 n N i , p ( u ) P i \mathbf{C}(u)=\sum_{i=0}^nN_{i,p}(u)\mathbf{P}_i
C ( u ) = i = 0 ∑ n N i , p ( u ) P i
其中,N i , p ( u ) N_{i,p}(u) N i , p ( u )
将控制点 P i \mathbf{P}_i P i
P i = [ x i y i z i 1 ] \mathbf{P}_i=\left[\begin{array}{c}x_i\\y_i\\z_i\\1\end{array}\right]
P i = ⎣ ⎢ ⎢ ⎢ ⎡ x i y i z i 1 ⎦ ⎥ ⎥ ⎥ ⎤
我们可以将这个 P i \mathbf{P}_i P i P i \mathbf{P}_i P i w i w_i w i
P i w = [ w i x i w i y i w i z i w i ] \mathbf{P}_{i}^{w}=\left[\begin{array}{c}w_{i}x_{i}\\w_{i}y_{i}\\w_{i}z_{i}\\w_{i}\end{array}\right]
P i w = ⎣ ⎢ ⎢ ⎢ ⎡ w i x i w i y i w i z i w i ⎦ ⎥ ⎥ ⎥ ⎤
注意,P i w \mathbf{P}_{i}^{w} P i w P i \mathbf{P}_{i} P i
C w ( u ) = ∑ i = 0 n N i , p ( u ) P i w = ∑ i = 0 n N i , p ( u ) [ w i x i w i y i w i z i w i ] = [ ∑ i = 0 n N i , p ( u ) ( w i x i ) ∑ i = 0 n N i , p ( u ) ( w i y i ) ∑ i = 0 n N i , p ( u ) ( w i z i ) ∑ i = 0 n N i , p ( u ) w i ] \mathbf{C}^w(u)=\sum\limits_{i=0}^nN_{i,p}(u)\mathbf{P}_i^w=\sum\limits_{i=0}^nN_{i,p}(u)\left[\begin{array}{c}w_ix_i\\w_iy_i\\w_iz_i\\w_i\end{array}\right]=\left[\begin{array}{c}\sum\limits_{i=0}^nN_{i,p}(u)(w_ix_i)\\\sum\limits_{i=0}^nN_{i,p}(u)(w_iy_i)\\\sum\limits_{i=0}^nN_{i,p}(u)(w_iz_i)\\\sum\limits_{i=0}^nN_{i,p}(u)w_i\end{array}\right]
C w ( u ) = i = 0 ∑ n N i , p ( u ) P i w = i = 0 ∑ n N i , p ( u ) ⎣ ⎢ ⎢ ⎢ ⎡ w i x i w i y i w i z i w i ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ i = 0 ∑ n N i , p ( u ) ( w i x i ) i = 0 ∑ n N i , p ( u ) ( w i y i ) i = 0 ∑ n N i , p ( u ) ( w i z i ) i = 0 ∑ n N i , p ( u ) w i ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
因此,点 C w ( u ) C^{w}(u) C w ( u )
现在,通过将 C w ( u ) C_w(u) C w ( u )
C ( u ) = [ ∑ i = 0 n N i , p ( u ) ( w i x i ) ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) ( w i y i ) ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) ( w i z i ) ∑ i = 0 n N i , p ( u ) w i 1 ] = ∑ i = 0 n N i , p ( u ) w i ∑ j = 0 n N j , p ( u ) w j [ x i y i z i 1 ] \mathbf{C}(u)=\begin{bmatrix}\frac{\sum_{i=0}^nN_{i,p}(u)(w_ix_i)}{\sum_{i=0}^nN_{i,p}(u)w_i}\\\frac{\sum_{i=0}^nN_{i,p}(u)(w_iy_i)}{\sum_{i=0}^nN_{i,p}(u)w_i}\\\frac{\sum_{i=0}^nN_{i,p}(u)(w_iz_i)}{\sum_{i=0}^nN_{i,p}(u)w_i}\\1\end{bmatrix}=\sum_{i=0}^n\frac{N_{i,p}(u)w_i}{\sum_{j=0}^nN_{j,p}(u)w_j}\begin{bmatrix}x_i\\y_i\\z_i\\1\end{bmatrix}
C ( u ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) ( w i x i ) ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) ( w i y i ) ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) ( w i z i ) 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = i = 0 ∑ n ∑ j = 0 n N j , p ( u ) w j N i , p ( u ) w i ⎣ ⎢ ⎢ ⎢ ⎡ x i y i z i 1 ⎦ ⎥ ⎥ ⎥ ⎤
最后,我们得到以下形式:
C ( u ) = 1 ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) w i P i \mathbf{C}(u)=\frac{1}{\sum_{i=0}^nN_{i,p}(u)w_i}\sum_{i=0}^nN_{i,p}(u)w_i\mathbf{P}_i
C ( u ) = ∑ i = 0 n N i , p ( u ) w i 1 i = 0 ∑ n N i , p ( u ) w i P i
上式是由控制点P 0 , P 1 , . . . P n \mathbf{P}_{0}, \mathbf{P}_{1}, ...\mathbf{P}_{n} P 0 , P 1 , . . . P n p p p U = u 0 , u 1 , . . . , u m U = {u_0, u_1, ..., u_m } U = u 0 , u 1 , . . . , u m w 0 , w 1 , . . . , w n w_0,w_1,...,w_n w 0 , w 1 , . . . , w n
Tips: 由于权重 w i w_i w i P i \mathbf{P}_i P i
一般情况下,权重w i w_i w i w i w_i w i P i \mathbf{P}_i P i P i \mathbf{P}_i P i u u u
从上述定义式中,我们可以立即得出两个结论:
如果所有的权重都等于1,那么一个NURBS曲线将简化为一个B样条曲线。 1 ∑ i = 0 n N i , p ( u ) w i \frac1{\sum_{i=0}^{n}N_{i,p}(u)w_{i}} ∑ i = 0 n N i , p ( u ) w i 1
NURBS曲线是有理曲线 N i , p ( u ) w i N_{i,p}(u)w_{i} N i , p ( u ) w i p p p p i \mathbf{p}_i p i 1 ∑ i = 0 n N i , p ( u ) w i \frac1{\sum_{i=0}^{n}N_{i,p}(u)w_{i}} ∑ i = 0 n N i , p ( u ) w i 1 p p p P i \mathbf{P}_i P i p p p NURBS 曲线C ( u ) C(u) C ( u )
这两个结论表明B样条曲线是NURBS曲线的特殊情况。此外,由于NURBS曲线是有理的,因此圆、椭圆和许多其他用B样条无法表示的曲线现在都可以通过NURBS曲线定义。
NURBS曲线是特殊类型的曲线吗?事实证明它们并不是。实际上,它们只是B样条曲线的另一面。
控制点P i W = ( w i x i , w i y i , w i z i , w i ) \mathbf{P}^{W}_{i}=(\begin{array}{ccc}w_{i}x_{i},&w_{i}y_{i},&w_{i}z_{i},&w_{i}\end{array}) P i W = ( w i x i , w i y i , w i z i , w i ) C ( u ) C(u) C ( u )
C w ( u ) = ∑ i = 0 n N i , p ( u ) P i w = ∑ i = 0 n N i , p ( u ) [ w i x i w i y i w i z i w i ] = [ ∑ i = 0 n N i , p ( u ) ( w i x i ) ∑ i = 0 n N i , p ( u ) ( w i y i ) ∑ i = 0 n N i , p ( u ) ( w i z i ) ] \mathbf{C}^w(u)=\sum\limits_{i=0}^nN_{i,p}(u)\mathbf{P}_i^w=\sum\limits_{i=0}^nN_{i,p}(u)\left[\begin{array}{c}w_ix_i\\w_iy_i\\w_iz_i\\w_i\end{array}\right]=\left[\begin{array}{c}\sum\limits_{i=0}^nN_{i,p}(u)(w_ix_i)\\\sum\limits_{i=0}^nN_{i,p}(u)(w_iy_i)\\\sum\limits_{i=0}^nN_{i,p}(u)(w_iz_i)\end{array}\right]
C w ( u ) = i = 0 ∑ n N i , p ( u ) P i w = i = 0 ∑ n N i , p ( u ) ⎣ ⎢ ⎢ ⎢ ⎡ w i x i w i y i w i z i w i ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ i = 0 ∑ n N i , p ( u ) ( w i x i ) i = 0 ∑ n N i , p ( u ) ( w i y i ) i = 0 ∑ n N i , p ( u ) ( w i z i ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
齐次坐标的几何解释:通过将前三个坐标分量除以第四个坐标相当于将四维点投影到平面 w = 1 w = 1 w = 1
上述曲线定义中,通过将前三个坐标除以第四个坐标,可以将B样条曲线定义转换为NURBS曲线定义。
所以我们有结论:三维空间中的NURBS曲线仅仅是四维空间中B样条曲线的投影。
给定n + 1 n+1 n + 1 P 0 , P 1 , … , P n \mathbf{P}_0,\mathbf{P}_1,\ldots,\mathbf{P}_n P 0 , P 1 , … , P n w i w_i w i w i > = 0 w_i >= 0 w i > = 0 m + 1 m+1 m + 1 U = u 0 , u 1 , . . . , u m U = { u_0, u_1, ..., u_m } U = u 0 , u 1 , . . . , u m p p p
C ( u ) = ∑ i = 0 n R i , p ( u ) P i \mathbf{C}(u)=\sum_{i=0}^nR_{i,p}(u)\mathbf{P}_i
C ( u ) = i = 0 ∑ n R i , p ( u ) P i
R i , p ( u ) R_{i,p}(u) R i , p ( u )
R i , p ( u ) = N i , p ( u ) w i ∑ j = 0 n N j , p ( u ) w j R_{i,p}(u)=\frac{N_{i,p}(u)w_i}{\sum_{j=0}^nN_{j,p}(u)w_j}
R i , p ( u ) = ∑ j = 0 n N j , p ( u ) w j N i , p ( u ) w i
由于NURBS曲线是B样条的泛化,它应该具有B样条的所有性质。
以下是NURBS曲线基函数最重要的性质
R i , p ( u ) R_{i,p}(u) R i , p ( u ) u u u p p p 非负性:对于任意 i i i p p p R i , p ( u ) R_{i,p}(u) R i , p ( u ) 局部支撑: R i , p ( u ) R_{i,p}(u) R i , p ( u ) [ u i , u i + p + 1 ) [u_i, u_{i+p+1}) [ u i , u i + p + 1 )
因为 N i , p ( u ) N_{i,p}(u) N i , p ( u ) [ u i , u i + p + 1 ) [u_i, u_{i+p+1}) [ u i , u i + p + 1 ) R i , p ( u ) R_{i,p}(u) R i , p ( u ) w i w_i w i
在节点区间 [ u i , u i + 1 ) [u_i, u_{i+1}) [ u i , u i + 1 ) p + 1 p+1 p + 1 p p p R i − p , p ( u ) R_{i-p,p}(u) R i − p , p ( u ) R i − p + 1 , p ( u ) R_{i-p+1,p}(u) R i − p + 1 , p ( u ) R i − p + 2 , p ( u ) R_{i-p+2,p}(u) R i − p + 2 , p ( u ) R i , p ( u ) R_{i,p}(u) R i , p ( u ) 单位分割:在区间 [ u i , u i + 1 ) [u_i, u_{i+1}) [ u i , u i + 1 ) p p p :如果节点数为m + 1 m+1 m + 1 p p p p p p n + 1 n+1 n + 1 m = n + p + 1 m=n+p+1 m = n + p + 1 :基函数 R i , p ( u ) R_{i,p}(u) R i , p ( u ) p p p [ u i , u i + p + 1 ) [u_i, u_{i+p+1}) [ u i , u i + p + 1 ) 在一个重数为 k k k R i , p ( u ) R_{i,p}(u) R i , p ( u ) C p − k C^{p-k} C p − k 如果对任意i i i w i = c w_i = c w i = c c c c R i , p ( u ) = N i , p ( u ) R_{i,p}(u)=N_{i,p}(u) R i , p ( u ) = N i , p ( u ) c = 1 c = 1 c = 1
下面列出了NURBS曲线的重要特性。
与B样条曲线一样,NURBS曲线可以是O p e n Open O p e n C l a m p e d Clamped C l a m p e d C l o s e d Closed C l o s e d p + 1 p+1 p + 1 p + 1 p+1 p + 1 [ 0 , 1 ] [0,1] [ 0 , 1 ] C l a m p e d Clamped C l a m p e d
NURBS曲线 C ( u ) C(u) C ( u ) 是一个分段曲线,其中每个曲线段都是一个次数为 p p p
NURBS曲线必须满足 m = n + p + 1 m = n + p + 1 m = n + p + 1
C l a m p e d Clamped C l a m p e d C ( u ) C(u) C ( u ) P 0 P_0 P 0 P n P_n P n
强凸包性质:**NURBS曲线位于其控制点定义的凸包内。**并且,如果u u u [ u i , u i + 1 ) [u_i,u_{i+1}) [ u i , u i + 1 ) C ( u ) C(u) C ( u ) P i − p , P i − p + 1 , . . . , P i P_{i-p}, P_{i-p+1}, ..., P_i P i − p , P i − p + 1 , . . . , P i
NURBS基函数的权重必须是非负的 ,如果其中一些是负数,则强凸包性质甚至凸包性质都有可能不满足。
在下面,左图是一个2次NURBS曲线,n = 2 , m = 5 n = 2,m = 5 n = 2 , m = 5
局部修改特性:改变控制点 P i \mathbf{P}_i P i C ( u ) C(u) C ( u ) [ u i , u i + p + 1 ) [u_i, u_{i+p+1}) [ u i , u i + p + 1 ) 。
这是基于B样条基函数的局部修改特性得出的。回想一下,R i , p ( u ) R_{i,p}(u) R i , p ( u ) [ u i , u i + p + 1 ) [u_i,u_{i+p+1}) [ u i , u i + p + 1 ) u u u R i , p ( u ) R_{i,p}(u) R i , p ( u ) p ( u ) \mathbf{p}(u) p ( u ) R i , p ( u ) p ( u ) R_{i,p}(u)\mathbf{p}(u) R i , p ( u ) p ( u ) u u u R i , p ( u ) R_{i,p}(u) R i , p ( u ) R i , p ( u ) p ( u ) R_{i,p}(u)\mathbf{p}(u) R i , p ( u ) p ( u ) C ( u ) C(u) C ( u )
这种局部修改方案对曲线设计非常重要,因为我们可以在局部修改曲线而不会在全局范围内改变形状。此外,如果需要微调曲线形状,可以插入更多的节点(或者更多的控制点),以便受影响的区域可以被限制在非常窄的范围内。
如果 u u u k k k C ( u ) C(u) C ( u ) C p − k C^{p-k} C p − k 如果 u u u C ( u ) C(u) C ( u ) p p p 如果 u u u R i , p ( u ) R_{i,p}(u) R i , p ( u ) R i , p ( u ) R_{i,p}(u) R i , p ( u ) C p − k C^{p-k} C p − k C ( u ) C(u) C ( u ) C p − k C^{p-k} C p − k
变差缩减特性:
B样条曲线和贝塞尔曲线是NURBS曲线的特殊情况
如果所有的权重都相等,那么NURBS曲线就变成了B样条曲线。n = p n = p n = p n n n 2 ( p + 1 ) = 2 ( n + 1 ) 2(p + 1) = 2(n + 1) 2 ( p + 1 ) = 2 ( n + 1 ) p + 1 p + 1 p + 1 p + 1 p+1 p + 1 c l a m p e d clamped c l a m p e d
投影变换不变性
如果将投影变换应用于NURBS曲线,则结果可以由其经过投影变换后的控制点构造而成。当我们想要对 NURBS 曲线应用几何变换 甚至投影变换 时,我们可以将变换应用于控制点,而转换后的 NURBS 曲线由转换后的控制点定义。因此,无需直接对曲线进行变换。注意,贝塞尔曲线和B样条曲线只满足仿射不变性质,而不是这种投影不变性质。这是因为只有NURBS曲线涉及投影变换。
NURBS曲线的基函数为
R i , p ( u ) = N i , p ( u ) w i ∑ j = 0 n N j , p ( u ) w j R_{i,p}(u)=\frac{N_{i,p}(u)w_i}{\sum_{j=0}^nN_{j,p}(u)w_j}
R i , p ( u ) = ∑ j = 0 n N j , p ( u ) w j N i , p ( u ) w i
因此,增加和减少w i w_i w i R i , p ( u ) R_{i,p}(u) R i , p ( u ) 更准确地说,增加w i w_i w i p i \mathbf{p}_i p i
并且,曲线上所有受影响的点也将朝向p i \mathbf{p}_i p i w i w_i w i p i \mathbf{p}_i p i w i w_i w i p i \mathbf{p}_i p i
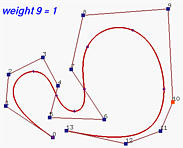
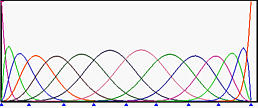
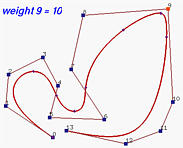
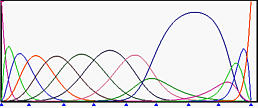
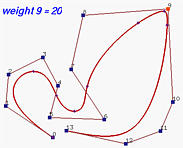
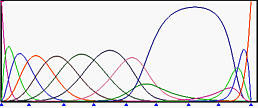
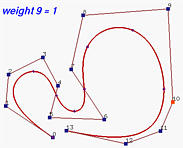
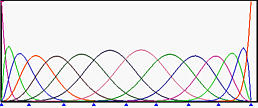
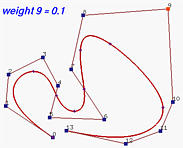
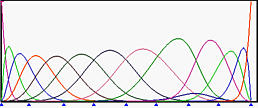
下图显示了一个6次NURBS曲线及其基函数。所选观察控制点为 p 9 \mathbf{p}_9 p 9 w 9 w_9 w 9 p 9 \mathbf{p}_9 p 9 w 9 w_9 w 9 R 9 , 6 ( u ) R_{9,6}(u) R 9 , 6 ( u )
下面,我们将w 9 w_9 w 9 R 9 , 6 ( u ) R_{9,6}(u) R 9 , 6 ( u ) p 9 \mathbf{p}_9 p 9 w 9 w_9 w 9 p 9 \mathbf{p}_9 p 9
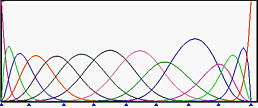
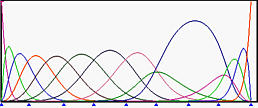
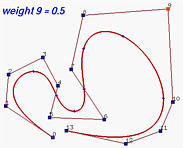
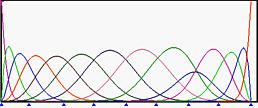
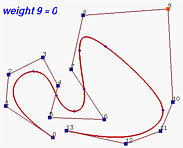
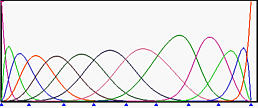
再来看看相反的效果。以下是所有权重都为1的初始情况。然后,w 9 w_9 w 9 这将曲线推离控制点 p 9 \mathbf{p}_9 p 9 R 9 , 6 ( u ) R_{9,6}(u) R 9 , 6 ( u ) p 9 \mathbf{p}_9 p 9 w 9 w_9 w 9 w 9 w_9 w 9 w 9 w_9 w 9 R 9 , 6 ( u ) R_{9,6}(u) R 9 , 6 ( u ) p 9 \mathbf{p}_9 p 9
因此,我们有以下结论:
增加( 或减少 )权重 w i w_i w i p i \mathbf{p}_i p i w i w_i w i p i \mathbf{p}_i p i w i w_i w i p i \mathbf{p}_i p i
我们想要更准确地分析改变控制点权重的影响。
NURBS曲线的定义:
C ( u ) = 1 ∑ i = 0 n N i , p ( u ) w i ∑ i = 0 n N i , p ( u ) w i P i \mathbf{C}(u)=\frac{1}{\sum_{i=0}^{n}N_{i,p}(u)w_{i}}\sum_{i=0}^{n}N_{i,p}(u)w_{i}\mathbf{P}_{i}
C ( u ) = ∑ i = 0 n N i , p ( u ) w i 1 i = 0 ∑ n N i , p ( u ) w i P i
我们选择控制点 P k P_k P k w k w_k w k
由于 P k P_k P k N k , p ( u ) N_{k,p}(u) N k , p ( u ) [ u k , u k + p + 1 ) [u_k, u_{k+p+1}) [ u k , u k + p + 1 ) C ( u ) C(u) C ( u ) u u u [ u k , u k + p + 1 ) [u_k, u_{k+p+1}) [ u k , u k + p + 1 )
将涉及w k w_k w k
C ( u ) = 1 N k , p ( u ) w k + ∑ i ≠ k n N i , p ( u ) w i ( N k , p ( u ) w k P k + ∑ i ≠ k n N i , p ( u ) w i P i ) \mathbf{C}(u)=\frac{1}{N_{k,p}(u)w_{k}+\sum_{i\neq k}^{n}N_{i,p}(u)w_{i}}\left(N_{k,p}(u)w_{k}\mathbf{P}_{k}+\sum_{i\neq k}^{n}N_{i,p}(u)w_{i}\mathbf{P}_{i}\right)
C ( u ) = N k , p ( u ) w k + ∑ i = k n N i , p ( u ) w i 1 ⎝ ⎛ N k , p ( u ) w k P k + i = k ∑ n N i , p ( u ) w i P i ⎠ ⎞
我们简化一下这个公式,令:
A = N k , p ( u ) w k B = ∑ i ≠ k N i , p ( u ) w i X = ∑ i ≠ k n N i , p ( u ) w i P i \begin{aligned}&A=N_{k,p}(u)w_{k}\\&B=\sum_{i\neq k}N_{i,p}(u)w_{i}\\&\mathbf{X}=\sum_{i\neq k}^{n}N_{i,p}(u)w_{i}\mathbf{P}_{i}\end{aligned}
A = N k , p ( u ) w k B = i = k ∑ N i , p ( u ) w i X = i = k ∑ n N i , p ( u ) w i P i
上式曲线的定义变成如下:
C ( u ) = 1 A + B ( A P k + X ) \mathbf{C}(u)=\frac{1}{A+B}(A\mathbf{P}_{k}+\mathbf{X})
C ( u ) = A + B 1 ( A P k + X )
考虑首先 w k = 0 w_k = 0 w k = 0 A = 0 \mathbf{A} = 0 A = 0 C 0 ( u ) C^0(u) C 0 ( u )
C 0 ( u ) = X B \mathbf{C}^0(u)=\frac{\mathbf{X}}{B}
C 0 ( u ) = B X
现在计算从这个基本点 C 0 ( u ) C^0(u) C 0 ( u ) w k w_k w k C ( 𝑢 ) C(𝑢) C ( u )
C ( u ) − C 0 ( u ) = 1 A + B ( A P k + X ) − X B = A A + B ( P k − X B ) = A A + B ( P k − C 0 ( u ) ) \begin{aligned}
\mathbf{C}(u)-\mathbf{C}^{0}(u)& =\frac{1}{A+B}(A\mathbf{P}_{k}+\mathbf{X})-\frac{\mathbf{X}}{B} \\
&={\frac{A}{A+B}}\left(\mathbf{P}_{k}-{\frac{\mathbf{X}}{B}}\right) \\
&=\frac{A}{A+B}\left(\mathbf{P}_{k}-\mathbf{C}^{0}(u)\right)
\end{aligned}
C ( u ) − C 0 ( u ) = A + B 1 ( A P k + X ) − B X = A + B A ( P k − B X ) = A + B A ( P k − C 0 ( u ) )
这意味着向量 C ( u ) − C 0 ( u ) C(u)-C^0(u) C ( u ) − C 0 ( u ) C k − C 0 ( u ) C_k-C^0(u) C k − C 0 ( u ) A / ( A + B ) A/(A+B) A / ( A + B )
对于 [ u k , u k + p + 1 ) [u_k, u_{k+p+1}) [ u k , u k + p + 1 ) u u u C k C_k C k C 0 ( u ) C^0(u) C 0 ( u ) C ( u ) C(u) C ( u ) P k \mathbf{P}_k P k C 0 ( u ) C^0(u) C 0 ( u )
如果所有的权重都是非负的,那么 A A A B B B A / ( A + B ) A/(A+B) A / ( A + B ) 点 C ( u ) C(u) C ( u ) P k \mathbf{P}_k P k C 0 ( u ) C^0(u) C 0 ( u )
如果 w k w_k w k C ( u ) C(u) C ( u ) w k w_k w k
C ( u ) = 1 N k , p ( u ) w k + ∑ i ≠ k N i , p ( u ) w i ( N k , p ( u ) w k P k + ∑ i ≠ k n N i , p ( u ) w i P i ) = 1 N k , p ( u ) + 1 w k ∑ i ≠ k N i , p ( u ) w i ( N k , p ( u ) P k + 1 w k ∑ i ≠ k n N i , p ( u ) w i P i ) \mathbf{C}(u)=\frac{1}{N_{k,p}(u)w_{k}+\sum_{i\neq k}N_{i,p}(u)w_{i}}\left(N_{k,p}(u)w_{k}\mathbf{P}_{k}+\sum_{i\neq k}^{n}N_{i,p}(u)w_{i}\mathbf{P}_{i}\right)\\=\frac{1}{N_{k,p}(u)+\frac{1}{w_{k}}\sum_{i\neq k}N_{i,p}(u)w_{i}}\left(N_{k,p}(u)\mathbf{P}_{k}+\frac{1}{w_{k}}\sum_{i\neq k}^{n}N_{i,p}(u)w_{i}\mathbf{P}_{i}\right)
C ( u ) = N k , p ( u ) w k + ∑ i = k N i , p ( u ) w i 1 ⎝ ⎛ N k , p ( u ) w k P k + i = k ∑ n N i , p ( u ) w i P i ⎠ ⎞ = N k , p ( u ) + w k 1 ∑ i = k N i , p ( u ) w i 1 ⎝ ⎛ N k , p ( u ) P k + w k 1 i = k ∑ n N i , p ( u ) w i P i ⎠ ⎞
如果w k w_k w k 1 w k \frac{1}{w_k} w k 1 P ( u ) \mathbf{P}(u) P ( u ) P k \mathbf{P}_k P k
因此我们有以下结论:
如果 w k w_k w k C ( u ) C(u) C ( u ) C 0 ( u ) C^0(u) C 0 ( u ) P k \mathbf{P}_k P k C 0 ( u ) C^0(u) C 0 ( u ) w k = 0 w_k = 0 w k = 0 u u u [ u k , u k + p + 1 ) [u_k, u_{k+p}+1) [ u k , u k + p + 1 ) w k w_k w k C ( u ) C(u) C ( u ) C 0 ( u ) C^0(u) C 0 ( u ) P k \mathbf{P}_k P k w k w_k w k C ( u ) C(u) C ( u ) C k C_k C k
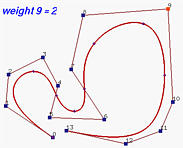
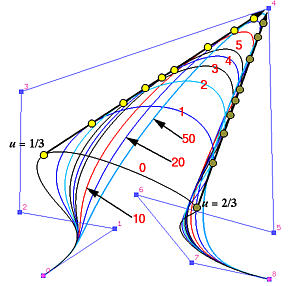
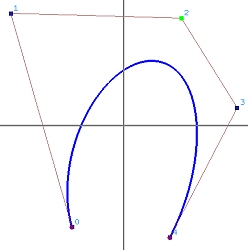
我们有一个由9个控制点(n = 8 n = 8 n = 8 m = 15 m = 15 m = 1 5
所选的控制点是 P 4 \mathbf{P}_4 P 4 P 4 \mathbf{P}_4 P 4 N 4 , 6 ( u ) N_{4,6}(u) N 4 , 6 ( u ) [ u 4 , u 4 + 6 + 1 ) = [ 0 , 1 ) [u_4, u_{4+6+1}) = [0,1) [ u 4 , u 4 + 6 + 1 ) = [ 0 , 1 ) w 4 w_4 w 4
对应于 u = 1 / 3 u = 1/3 u = 1 / 3 u = 2 / 3 u = 2/3 u = 2 / 3 w 4 = 0 w_4 = 0 w 4 = 0 w 4 w_4 w 4 w 4 w_4 w 4 P 4 \mathbf{P}_4 P 4 w 4 w_4 w 4 P 4 \mathbf{P}_4 P 4
注意,所有对应于 C ( 1 3 ) C(\frac{1}{3}) C ( 3 1 ) C 0 ( 1 3 ) C^0(\frac{1}{3}) C 0 ( 3 1 ) P 4 \mathbf{P}_4 P 4 C ( 2 3 ) C(\frac{2}{3}) C ( 3 2 ) C 0 ( 2 3 ) C^0(\frac{2}{3}) C 0 ( 3 2 ) P 4 \mathbf{P}_4 P 4
随着 w 4 w_4 w 4 C ( 1 3 ) C(\frac{1}{3}) C ( 3 1 ) C ( 2 3 ) C(\frac{2}{3}) C ( 3 2 ) w 4 w_4 w 4 C ( 1 3 ) C(\frac{1}{3}) C ( 3 1 ) C ( 2 3 ) C(\frac{2}{3}) C ( 3 2 ) P 4 \mathbf{P}_4 P 4
由于NURBS曲线是四维空间中的B样条曲线投影到三维空间的结果,因此对NURBS曲线进行节点插入是很容易的。
对NURBS曲线进行节点插入分为三个步骤:(1)将给定三维空间中的NURBS曲线转换为四维空间中的B样条曲线 (2)对这个四维B样条曲线执行节点插入 (3)将新的控制点集投影回三维空间,得到NURBS曲线的新的一组控制点。
假设我们有 n + 1 n + 1 n + 1 P 0 , P 1 , . . . , P n \mathbf{P}_0, \mathbf{P}_1, ..., \mathbf{P}_n P 0 , P 1 , . . . , P n w 0 , w 1 , . . . , w n w_0, w_1, ..., w_n w 0 , w 1 , . . . , w n U U U p p p P i = ( x i , y i , z i ) \mathbf{P}_i = (x_i, y_i, z_i) P i = ( x i , y i , z i )
那么,控制点 P i w = ( w i x i , w i y i , w i z i , w i ) \mathbf{P}^w_i = ( w_i x_i, w_i y_i, w_i z_i, w_i ) P i w = ( w i x i , w i y i , w i z i , w i ) 0 ≤ i ≤ n 0 \leq i \leq n 0 ≤ i ≤ n U U U p p p t t t Q i w = ( X i , Y i , Z i , W i ) Q^w_i = ( X_i, Y_i, Z_i, W_i ) Q i w = ( X i , Y i , Z i , W i ) 0 ≤ i ≤ n 0 \leq i \leq n 0 ≤ i ≤ n
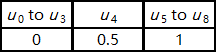
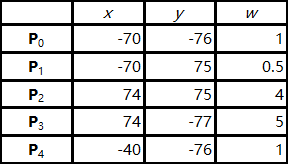
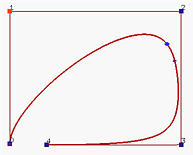
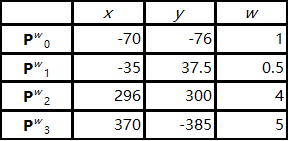
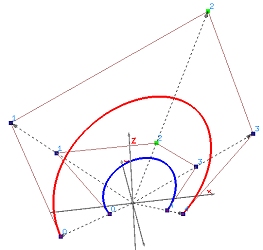
让我们来看一个例子。假设我们有 9 个结点
下面是在x y xy x y
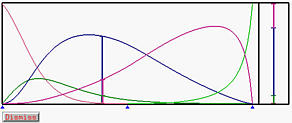
下图展示了曲线形状及其基础函数。
我们插入一个新的节点 t = 0.4 t = 0.4 t = 0 . 4 t t t [ u 3 , u 4 ) [u_3, u_4) [ u 3 , u 4 ) P 3 、 P 2 、 P 1 \mathbf{P}_3、\mathbf{P}_2、\mathbf{P}_1 P 3 、 P 2 、 P 1 P 0 \mathbf{P}_0 P 0 P i w \mathbf{P}^w_i P i w
注意,由于 P 4 \mathbf{P}_4 P 4 a 3 、 a 2 a_3、a_2 a 3 、 a 2 a 1 a_1 a 1
a 3 = t − u 3 u 6 − u 3 = 0.4 − 0 1 − 0 = 0.4 a 2 = t − u 2 u 5 − u 2 = 0.4 − 0 1 − 0 = 0.4 a 1 = t − u 1 u 4 − u 1 = 0.4 − 0 0.5 − 0 = 0.8 a_{3}=\frac{t-u_{3}}{u_{6}-u_{3}}=\frac{0.4-0}{1-0}=0.4\\a_{2}=\frac{t-u_{2}}{u_{5}-u_{2}}=\frac{0.4-0}{1-0}=0.4\\a_{1}=\frac{t-u_{1}}{u_{4}-u_{1}}=\frac{0.4-0}{0.5-0}=0.8 a 3 = u 6 − u 3 t − u 3 = 1 − 0 0 . 4 − 0 = 0 . 4 a 2 = u 5 − u 2 t − u 2 = 1 − 0 0 . 4 − 0 = 0 . 4 a 1 = u 4 − u 1 t − u 1 = 0 . 5 − 0 0 . 4 − 0 = 0 . 8
新的控制点Q 3 w , Q 2 w \mathbf{Q}^w_3, \mathbf{Q}^w_2 Q 3 w , Q 2 w Q 1 w \mathbf{Q}^w_1 Q 1 w
Q 3 w = ( 1 − a 3 ) P 2 w + a 3 P 3 w = ( 325.6 , 26 , 4.4 ) Q 2 w = ( 1 − a 2 ) P 1 w + a 2 P 2 w = ( 97.4 , 142.5 , 1.9 ) Q 1 w = ( 1 − a 1 ) P 0 w + a 1 P 1 w = ( − 42 , 14.8 , 0.6 ) \mathbf{Q}_{3}^{w}=(1-a_{3})\mathbf{P}_{2}^{w}+a_{3}\mathbf{P}_{3}^{w}=(325.6,26,4.4)\\\mathbf{Q}_{2}^{w}=(1-a_{2})\mathbf{P}_{1}^{w}+a_{2}\mathbf{P}_{2}^{w}=(97.4,142.5,1.9)\\\mathbf{Q}_{1}^{w}=(1-a_{1})\mathbf{P}_{0}^{w}+a_{1}\mathbf{P}_{1}^{w}=(-42,14.8,0.6)
Q 3 w = ( 1 − a 3 ) P 2 w + a 3 P 3 w = ( 3 2 5 . 6 , 2 6 , 4 . 4 ) Q 2 w = ( 1 − a 2 ) P 1 w + a 2 P 2 w = ( 9 7 . 4 , 1 4 2 . 5 , 1 . 9 ) Q 1 w = ( 1 − a 1 ) P 0 w + a 1 P 1 w = ( − 4 2 , 1 4 . 8 , 0 . 6 )
将这些控制点的前两个分量除以第三个分量投影回二维空间,得到
n e w P 3 = ( 74 , 5.9 ) w i t h w e i g h t 4.4 n e w P 2 = ( 51.3 , 75 ) w i t h w e i g h t 1.9 n e w P 1 = ( − 70 , 24.6 ) w i t h w e i g h t 0.6 \begin{array}{rcll}\mathrm{newP}_3&=&(74,5.9)&\mathrm{with~weight~4.4}\\\mathrm{newP}_2&=&(51.3,75)&\mathrm{with~weight~1.9}\\\mathrm{newP}_1&=&(-70,24.6)&\mathrm{with~weight~0.6}\end{array}
n e w P 3 n e w P 2 n e w P 1 = = = ( 7 4 , 5 . 9 ) ( 5 1 . 3 , 7 5 ) ( − 7 0 , 2 4 . 6 ) w i t h w e i g h t 4 . 4 w i t h w e i g h t 1 . 9 w i t h w e i g h t 0 . 6
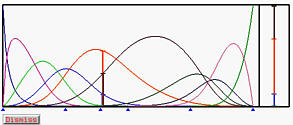
下图是生成的NURBS曲线及其基函数:
一旦我们知道如何插入节点,NURBS曲线的de Boor算法就简单了。
我们只需要将每个控制点乘以它的权重,将NURBS曲线转换为四维空间中的B样条曲线 ,在这个四维B样条曲线上执行de Boor算法,然后通过将控制点的前三个分量除以第四个分量,并将第四个分量作为新的权重,就可以将四维曲线投影回三维空间 。
将一个四维B样条曲线投影到 w = 1 w=1 w = 1 有理贝塞尔曲线 !
下面的左图显示了一个4阶有理贝塞尔曲线,右图显示了一个三维4阶贝塞尔曲线(红色)及其在超平面 w = 1 w=1 w = 1
由一组n + 1 n+1 n + 1 P 0 , P 1 , . . . , P n \mathbf{P}_0, \mathbf{P}_1, ..., \mathbf{P}_n P 0 , P 1 , . . . , P n w i w_i w i P i \mathbf{P}_i P i w i w_i w i P i w ( 0 < = i < = n ) \mathbf{P}^w_i (0 <= i <= n) P i w ( 0 < = i < = n ) n n n B n , 0 ( u ) , B n , 1 ( u ) , . . . , B n , n ( u ) B_{n,0}(u),B_{n,1}(u),...,B_{n,n}(u) B n , 0 ( u ) , B n , 1 ( u ) , . . . , B n , n ( u ) w = 1 w = 1 w = 1
C ( u ) = ∑ i = 0 n R i , n ( u ) P i \mathbf{C}(u)=\sum_{i=0}^nR_{i,n}(u)\mathbf{P}_i
C ( u ) = i = 0 ∑ n R i , n ( u ) P i
R i , n ( u ) R_{i,n}(u) R i , n ( u )
R i , n ( u ) = B n , i ( u ) w i ∑ j = 0 n B n , j ( u ) w j R_{i,n}(u)=\frac{B_{n,i}(u)w_i}{\sum_{j=0}^nB_{n,j}(u)w_j}
R i , n ( u ) = ∑ j = 0 n B n , j ( u ) w j B n , i ( u ) w i
这是NURBS曲线的一个特殊情况,称为有理Bézier 曲线。
由于有理Bézier曲线是NURBS曲线的一个特例 ,因此有理Bézier曲线满足所有NURBS曲线具有的重要性质。
然而,由于没有内部节点,有理Bézier曲线不具备局部修改的特性 ,这意味着修改控制点或其权重将导致整个曲线发生变化。修改控制点的权重将使曲线远离或朝向控制点。
由于贝塞尔曲线和B样条曲线是多项式曲线,只能表示抛物线。但NURBS和有理贝塞尔曲线是有理的,它们是否能表示椭圆、圆和双曲线,如果可以的话,应该如何做?
由三个不共线的控制点 P 0 = ( U 0 , V 0 ) , P 1 = ( U 1 , V 1 ) a n d P 2 = ( U 2 , V 2 ) \mathbf{P}_0=(U_0,V_0),\mathbf{P}_1=(U_1,V_1)\mathrm{~and~}\mathbf{P}_2=(U_2,V_2) P 0 = ( U 0 , V 0 ) , P 1 = ( U 1 , V 1 ) a n d P 2 = ( U 2 , V 2 ) 抛物线 。我们希望扩展这个概念,以定义椭圆和双曲线的部分。
假设圆锥曲线通过P 0 \mathbf{P}_0 P 0 P 2 \mathbf{P}_2 P 2 P 0 \mathbf{P}_0 P 0 P 2 \mathbf{P}_2 P 2 P 0 P 1 \mathbf{P}_0\mathbf{P}_1 P 0 P 1 P 1 P 2 \mathbf{P}_1\mathbf{P}_2 P 1 P 2
p ( x , y ) = a x 2 + 2 b x y + c y 2 + 2 d x + 2 e y + f = 0 p(x,y)=ax^2+2bxy+cy^2+2dx+2ey+f=0
p ( x , y ) = a x 2 + 2 b x y + c y 2 + 2 d x + 2 e y + f = 0
如果f f f f f f
a x 2 + 2 b x y + c y 2 + 2 d x + 2 e y + 1 = 0 ax^2+2bxy+cy^2+2dx+2ey+1=0
a x 2 + 2 b x y + c y 2 + 2 d x + 2 e y + 1 = 0
这样我们只有五个未知数!如果f f f P 0 \mathbf{P}_0 P 0 P 0 \mathbf{P}_0 P 0
a U 0 2 + 2 b U 0 V 0 + c V 0 2 + 2 d U 0 + 2 e V 0 + 1 = 0 aU_0^2+2bU_0V_0+cV_0^2+2dU_0+2eV_0+1=0
a U 0 2 + 2 b U 0 V 0 + c V 0 2 + 2 d U 0 + 2 e V 0 + 1 = 0
方程的梯度计算如下:
∇ p ( x , y ) = ⟨ 2 a x + 2 b y + 2 d , 2 b x + 2 c y + 2 e ⟩ \nabla_{p(x,y)}=\langle2ax+2by+2d,2bx+2cy+2e\rangle
∇ p ( x , y ) = ⟨ 2 a x + 2 b y + 2 d , 2 b x + 2 c y + 2 e ⟩
切线和梯度在点P 0 = ( U 0 , V 0 ) \mathbf{P}_0=(U_0,V_0) P 0 = ( U 0 , V 0 )
由于梯度的斜率为
b U 0 + c V 0 + e a U 0 + b V 0 + d \frac{\mathrm{b}U_0+\mathrm{c}V_0+\mathrm{e}}{\mathrm{a}U_0+\mathrm{b}V_0+\mathrm{d}}
a U 0 + b V 0 + d b U 0 + c V 0 + e
在点P 0 = ( U 0 , V 0 ) \mathbf{P}_0=(U_0,V_0) P 0 = ( U 0 , V 0 )
− a U 0 + b V 0 + d b U 0 + c V 0 + e -\frac{\mathrm{a}U_0+\mathrm{b}V_0+\mathrm{d}}{\mathrm{b}U_0+\mathrm{c}V_0+\mathrm{e}}
− b U 0 + c V 0 + e a U 0 + b V 0 + d
由于P 0 P 1 \mathbf{P}_0\mathbf{P}_1 P 0 P 1 P 0 \mathbf{P}_0 P 0 P 0 P 1 \mathbf{P}_0\mathbf{P}_1 P 0 P 1 ( V 1 − V 0 ) / ( U 1 − U 0 ) (V_1-V_0)/(U_1-U_0) ( V 1 − V 0 ) / ( U 1 − U 0 )
V 1 − V 0 U 1 − U 0 = − a U 0 + b V 0 + d b U 0 + c V 0 + e \frac{V_1-V_0}{U_1-U_0}=-\frac{aU_0+bV_0+d}{bU_0+cV_0+e}
U 1 − U 0 V 1 − V 0 = − b U 0 + c V 0 + e a U 0 + b V 0 + d
由于圆锥曲线也通过 P 2 \mathbf{P}_2 P 2
a U 2 2 + 2 b U 2 V 2 + c V 2 2 + 2 d U 2 + 2 e V 2 + 1 = 0 aU_2^2+2bU_2V_2+cV_2^2+2dU_2+2eV_2+1=0
a U 2 2 + 2 b U 2 V 2 + c V 2 2 + 2 d U 2 + 2 e V 2 + 1 = 0
圆锥曲线在P 2 \mathbf{P}_2 P 2 P 1 P 2 \mathbf{P}_1\mathbf{P}_2 P 1 P 2
V 2 − V 1 U 2 − U 1 = − a U 2 + b V 2 + d b U 2 + c V 2 + e \frac{V_{2}-V_{1}}{U_{2}-U_{1}}=-\frac{aU_{2}+bV_{2}+d}{bU_{2}+cV_{2}+e}
U 2 − U 1 V 2 − V 1 = − b U 2 + c V 2 + e a U 2 + b V 2 + d
现在,我们有四个方程。如果我们能找到另一个条件,我们将得到五个带有五个未知数的线性方程。解这个线性方程组将得到所有五个系数,从而唯一确定了圆锥曲线。
一种方式是再将一个点的坐标代入方程,得到一个类似于控制点 P 0 \mathbf{P}_0 P 0 P 2 \mathbf{P}_2 P 2
但是,这个点在哪里 ?
这个点应该位于三个控制点构成的三角形内部,以保持凸包性质。
一种方法是允许这个点位于 P 1 \mathbf{P}_1 P 1 P 0 P 2 \mathbf{P}_0\mathbf{P}_2 P 0 P 2
很容易看出,如果选择的点从P 0 P 2 \mathbf{P}_0\mathbf{P}_2 P 0 P 2 P 1 \mathbf{P}_1 P 1 P 1 \mathbf{P}_1 P 1 P 1 \mathbf{P}_1 P 1 P 1 \mathbf{P}_1 P 1 P 1 \mathbf{P}_1 P 1
由于我们只需要一个点,该点受控制点P 1 \mathbf{P}_1 P 1 P 0 、 P 1 \mathbf{P}_0、\mathbf{P}_1 P 0 、 P 1 P 2 \mathbf{P}_2 P 2 1 、 w 1、w 1 、 w 1 1 1 P 1 \mathbf{P}_1 P 1
B 2 , 0 ( u ) = ( 1 − u ) 2 B 2 , 1 ( u ) = 2 ( 1 − u ) u B 2 , 2 ( u ) = u 2 \begin{aligned}&B_{2,0}(u)=&&(1-u)^2\\&B_{2,1}(u)=&&2(1-u)u\\&B_{2,2}(u)=&&u^{2}\end{aligned}
B 2 , 0 ( u ) = B 2 , 1 ( u ) = B 2 , 2 ( u ) = ( 1 − u ) 2 2 ( 1 − u ) u u 2
这个二次有理贝塞尔曲线的方程表示为:
C ( u ) = 1 ( 1 − u ) 2 + 2 ( 1 − u ) u w + u 2 ( ( 1 − u ) 2 P 0 + 2 ( 1 − u ) u w P 1 + u 2 P 2 ) \mathbf{C}(u)=\frac{1}{(1-u)^{2}+2(1-u)uw+u^{2}}\Big((1-u)^{2}\mathbf{P}_{0}+2(1-u)uw\mathbf{P}_{1}+u^{2}\mathbf{P}_{2}\Big)
C ( u ) = ( 1 − u ) 2 + 2 ( 1 − u ) u w + u 2 1 ( ( 1 − u ) 2 P 0 + 2 ( 1 − u ) u w P 1 + u 2 P 2 )
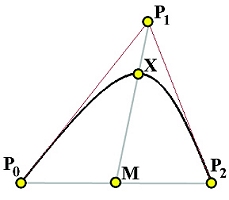
我们将P 0 \mathbf{P}_0 P 0 P 2 \mathbf{P}_2 P 2 x x x P 0 P 2 \mathbf{P}_0\mathbf{P}_2 P 0 P 2
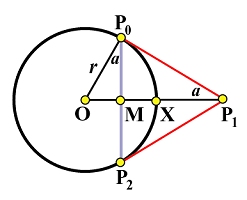
如下图,我们有P 0 = − P 2 \mathbf{P}_0 = -\mathbf{P}_2 P 0 = − P 2 P 0 P 2 \mathbf{P}_0\mathbf{P}_2 P 0 P 2 M \mathbf{M} M M P 1 \mathbf{M}\mathbf{P}_1 M P 1 X \mathbf{X} X
计算一下u = 0.5 u=0.5 u = 0 . 5 C ( u ) C(u) C ( u )
C ( 0.5 ) = w 1 + w P 1 \mathbf{C}(0.5)=\frac{w}{1+w}\mathbf{P}_1
C ( 0 . 5 ) = 1 + w w P 1
由于C ( 0.5 ) C(0.5) C ( 0 . 5 ) X \mathbf{X} X X \mathbf{X} X P 1 \mathbf{P}_1 P 1 M \mathbf{M} M
∣ M X → ∣ / ∣ M P → 1 ∣ = w 1 + w |\overrightarrow{MX}|/|\overrightarrow{MP}_1| = \frac{w}{1+w}
∣ M X ∣ / ∣ M P 1 ∣ = 1 + w w
如果w = 1 w=1 w = 1
∣ M X → ∣ / ∣ M P → 1 ∣ = w 1 + w = 1 / 2 |\overrightarrow{MX}|/|\overrightarrow{MP}_1| = \frac{w}{1+w} = 1/2
∣ M X ∣ / ∣ M P 1 ∣ = 1 + w w = 1 / 2
此时点X \mathbf{X} X M P 1 \mathbf{M}\mathbf{P}_1 M P 1
从给定圆锥曲线外的点 A \mathbf{A} A X \mathbf{X} X Y \mathbf{Y} Y X Y \mathbf{X}\mathbf{Y} X Y C \mathbf{C} C B \mathbf{B} B D \mathbf{D} D B \mathbf{B} B A X Y \mathbf{A}\mathbf{X}\mathbf{Y} A X Y A 、 B 、 C \mathbf{A}、\mathbf{B}、\mathbf{C} A 、 B 、 C A \mathbf{A} A D \mathbf{D} D
根据投影的关系,我们有:
∣ D C ∣ ∣ C B ∣ = ∣ D A ∣ ∣ A B ∣ \frac{|\mathrm{DC}|}{|\mathrm{CB}|}=\frac{|\mathrm{DA}|}{|\mathrm{AB}|}
∣ C B ∣ ∣ D C ∣ = ∣ A B ∣ ∣ D A ∣
通过变换可以得到如下关系:
∣ A B ∣ ∣ C B ∣ = ∣ D A ∣ ∣ D C ∣ \frac{|\mathrm{AB}|}{|\mathrm{CB}|}=\frac{|\mathrm{DA}|}{|\mathrm{DC}|}
∣ C B ∣ ∣ A B ∣ = ∣ D C ∣ ∣ D A ∣
因为 ∣ C A ∣ = ∣ C B ∣ + ∣ B A ∣ |\mathbf{CA}| = |\mathbf{CB}| + |\mathbf{BA}| ∣ C A ∣ = ∣ C B ∣ + ∣ B A ∣ ∣ C B ∣ / ∣ C A ∣ |\mathbf{CB}|/|\mathbf{CA}| ∣ C B ∣ / ∣ C A ∣
∣ C B ∣ ∣ C A ∣ = ∣ C B ∣ ∣ C B ∣ + ∣ B A ∣ = 1 1 + ∣ B A ∣ ∣ C B ∣ = 1 1 + ∣ D A ∣ ∣ D C ∣ \frac{|\mathrm{CB}|}{|\mathrm{CA}|}=\frac{|\mathrm{CB}|}{|\mathrm{CB}|+|\mathrm{BA}|}=\frac{1}{1+\frac{|\mathrm{BA}|}{|\mathrm{CB}|}}=\frac{1}{1+\frac{|\mathrm{DA}|}{|\mathrm{DC}|}}
∣ C A ∣ ∣ C B ∣ = ∣ C B ∣ + ∣ B A ∣ ∣ C B ∣ = 1 + ∣ C B ∣ ∣ B A ∣ 1 = 1 + ∣ D C ∣ ∣ D A ∣ 1
如果曲线是一个椭圆(或者双曲线),我们有 ∣ D A ∣ > ∣ D C ∣ |DA|>|DC| ∣ D A ∣ > ∣ D C ∣ ∣ D A ∣ < ∣ D C ∣ |DA|<|DC| ∣ D A ∣ < ∣ D C ∣ ∣ C B ∣ / ∣ C A ∣ |CB|/|CA| ∣ C B ∣ / ∣ C A ∣
对于有理贝塞尔曲线,我们有P 0 = X , P 1 = A , P 2 = Y , M = C \mathbf{P}_{0}=\mathbf{X},\mathbf{P}_{1}=\mathbf{A},\mathbf{P}_{2}=\mathbf{Y},\mathbf{M}=\mathbf{C} P 0 = X , P 1 = A , P 2 = Y , M = C X = C ( 0.5 ) = B \mathbf{X}=\mathbf{C}(0.5)=\mathbf{B} X = C ( 0 . 5 ) = B
w 1 + w = ∣ M X ∣ ∣ M P 1 ∣ < 1 2 \frac{w}{1+w}=\frac{|\mathrm{MX}|}{|\mathrm{MP}_1|}<\frac{1}{2}
1 + w w = ∣ M P 1 ∣ ∣ M X ∣ < 2 1
这说明如果 w < 1 w < 1 w < 1 w > 1 w > 1 w > 1
我们有以下结论:
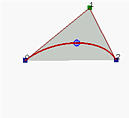
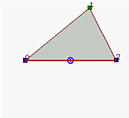
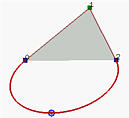
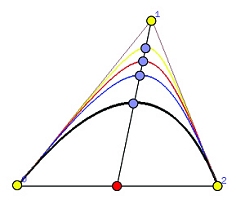
由三个非共线控制点P 0 , P 1 \mathbf{P}_0,\mathbf{P}_1 P 0 , P 1 P 2 \mathbf{P}_2 P 2 w w w w > 1 w>1 w > 1 w = 1 w=1 w = 1 w < 1 w<1 w < 1
最后,我们希望能够表示圆弧和圆。前者使用有理贝塞尔曲线,后者使用NURBS 。
由于**圆是椭圆的特例,它们可以使用度数为2的有理贝塞尔曲线表示,唯一的权重w < 1 w<1 w < 1
首先,我们知道控制多边形的两条边必须相等,即P 0 P 1 = P 1 P 2 \mathbf{P}_0\mathbf{P}_1=\mathbf{P}_1\mathbf{P}_2 P 0 P 1 = P 1 P 2
假设有理贝塞尔曲线表示的圆其圆心和半径分别为 O \mathbf{O} O r \mathbf{r} r
弦P 0 P 2 P_0P_2 P 0 P 2 M \mathbf{M} M M P 1 \mathbf{MP}_1 M P 1 X \mathbf{X} X P 1 \mathbf{P}_1 P 1 2 a 2a 2 a w w w ∣ M X ∣ / ∣ M P 1 ∣ = w / ( 1 + w ) |\mathrm{MX}|/|\mathrm{MP}_1|=w/(1+w) ∣ M X ∣ / ∣ M P 1 ∣ = w / ( 1 + w )
从直角三角形O M P 0 OMP_0 O M P 0 ∣ O M ∣ = r sin ( a ) |OM| = r \sin(a) ∣ O M ∣ = r sin ( a )
∣ M X ∣ = ∣ O X ∣ − ∣ O M ∣ = r − r sin ( a ) = r ( 1 − sin ( a ) ) |\mathrm{MX}|=|\mathrm{OX}|-|\mathrm{OM}|=r-r\sin(a)=r(1-\sin(a))
∣ M X ∣ = ∣ O X ∣ − ∣ O M ∣ = r − r sin ( a ) = r ( 1 − sin ( a ) )
根据直角三角形O P o P 1 OP_oP_1 O P o P 1 O P 1 = r / sin ( a ) \mathrm{OP}_1=r/\sin(a) O P 1 = r / sin ( a ) M P 1 MP_1 M P 1
∣ M P 1 ∣ = ∣ O P 1 ∣ − ∣ O M ∣ = r sin ( a ) − r sin ( a ) = r ( 1 − sin 2 ( a ) ) sin ( a ) |\mathrm{MP}_1|=|\mathrm{OP}_1|-|\mathrm{OM}|=\frac{r}{\sin(a)}-r\sin(a)=\frac{r(1-\sin^2(a))}{\sin(a)}
∣ M P 1 ∣ = ∣ O P 1 ∣ − ∣ O M ∣ = sin ( a ) r − r sin ( a ) = sin ( a ) r ( 1 − sin 2 ( a ) )
现在,我们可以使用∣ M X ∣ / ∣ M P 1 ∣ |\mathrm{MX}|/|\mathrm{MP}_1| ∣ M X ∣ / ∣ M P 1 ∣ w / ( 1 + w ) w/(1+w) w / ( 1 + w )
w 1 + w = ∣ M X ∣ ∣ M P 1 ∣ = sin ( a ) 1 + sin ( a ) \frac{w}{1+w}=\frac{|\mathrm{MX}|}{|\mathrm{MP}_1|}=\frac{\sin(a)}{1+\sin(a)}
1 + w w = ∣ M P 1 ∣ ∣ M X ∣ = 1 + sin ( a ) sin ( a )
求解 w w w 唯一权重值 w w w P 1 \mathbf{P}_1 P 1
w = sin ( a ) w=\sin(a) w = sin ( a )
这说明:给定三个控制点P 0 , P 1 P_{0},P_{1} P 0 , P 1 P 2 P_{2} P 2 P 0 P 1 = P 1 P 2 \mathsf{P}_0\mathsf{P}_1=\mathsf{P}_1\mathsf{P}_2 P 0 P 1 = P 1 P 2 𝑤 𝑤 w P 1 \mathbf{P}_1 P 1 𝑎 𝑎 a P 1 \mathbf{P}_1 P 1
有两个常见的例子:
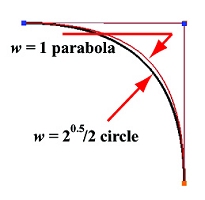
第一个例子是四分之一圆。点P 1 \mathbf{P}_1 P 1 a a a w = s i n ( 45 ° ) = 20.5 / 2 w = sin(45°) = 20.5/2 w = s i n ( 4 5 ° ) = 2 0 . 5 / 2 w = 1 w= 1 w = 1
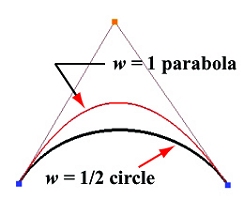
第二个例子是一个圆的三分之一。由于圆可以内切于一个等边三角形,这个圆的三分之一对应的角度为60度,因此,a a a w = s i n ( 30 ° ) = 1 / 2 w=sin(30°) = 1/2 w = s i n ( 3 0 ° ) = 1 / 2
我们可以取三个1 / 3 1/3 1 / 3 1 / 4 1/4 1 / 4
让我们首先考虑等边三角形的情况。
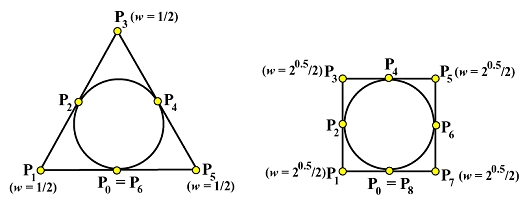
如上图左侧所示。每个等边三角形的顶点都是先前描述的权重为1 / 2 1/2 1 / 2 1 / 3 1/3 1 / 3 P 0 \mathbf{P}_0 P 0 P 1 \mathbf{P}_1 P 1 P 2 \mathbf{P}_2 P 2 1 / 3 1/3 1 / 3 P 2 \mathbf{P}_2 P 2 P 3 和 P 4 \mathbf{P}_4 P 4 1 / 3 1/3 1 / 3 P 4 \mathbf{P}_4 P 4 P 5 \mathbf{P}_5 P 5 P 6 = P 0 \mathbf{P}_6 = \mathbf{P}_0 P 6 = P 0
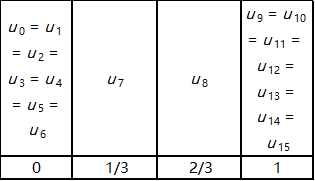
接下来,我们要研究节点。由于 n = 6 , p = 2 n = 6,p = 2 n = 6 , p = 2 m = 6 + 2 + 1 m = 6 + 2 + 1 m = 6 + 2 + 1 u 0 = u 1 = u 2 = 0 , u 7 = u 8 = u 9 = 1 u_0 = u_1 = u_2 = 0,u_7 = u_8 = u_9 = 1 u 0 = u 1 = u 2 = 0 , u 7 = u 8 = u 9 = 1
到目前为止,未知的节点是 u 3 , u 4 , u 5 u_3,u_4,u_5 u 3 , u 4 , u 5 u 6 u_6 u 6
一种方式是将1 / 3 1/3 1 / 3 2 / 3 2/3 2 / 3 [ 0 , 1 / 3 ] , [ 1 / 3 , 2 / 3 ] [0, 1/3],[1/3, 2/3] [ 0 , 1 / 3 ] , [ 1 / 3 , 2 / 3 ] [ 2 / 3 , 1 ] [2/3, 1] [ 2 / 3 , 1 ]
在上图中,你会看到控制点P 2 \mathbf{P}_2 P 2 1 / 3 1/3 1 / 3
我们如何让曲线通过一个控制点呢?可以采用de Boor 算法。当计算一个B样条/NURBS曲线上对应于u u u u u u u u u p p p p p p u u u P 2 \mathbf{P}_2 P 2
这个结论告诉我们,如果1 / 3 1/3 1 / 3
因此可以得到u 3 = u 4 = 1 / 3 u_3 = u_4 = 1/3 u 3 = u 4 = 1 / 3 u 5 = u 6 = 2 / 3 u_5 = u_6 = 2/3 u 5 = u 6 = 2 / 3
我们有结论:
要用等边三角形形定义一个完整的圆,我们要有节点0 , 0 , 0 , 1 / 3 , 1 / 3 , 2 / 3 , 2 / 3 , 1 , 1 , 1 0,0,0,1/3,1/3,2/3,2/3,1,1,1 0 , 0 , 0 , 1 / 3 , 1 / 3 , 2 / 3 , 2 / 3 , 1 , 1 , 1 要用一个正方形定义一个完整的圆,我们需要如图所示的九个控制点和节点向量0 , 0 , 0 , 1 / 4 , 1 / 4 , 1 / 2 , 1 / 2 , 3 / 4 , 3 / 4 , 1 , 1 , 1 0,0,0,1/4,1/4,1/2,1/2,3/4,3/4,1,1,1 0 , 0 , 0 , 1 / 4 , 1 / 4 , 1 / 2 , 1 / 2 , 3 / 4 , 3 / 4 , 1 , 1 , 1
那么,如何用一个有n n n


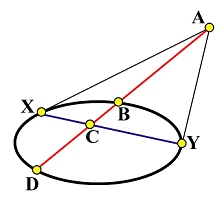 (a) Ellipse
(a) Ellipse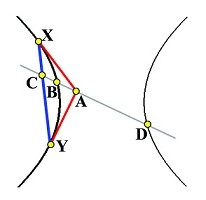 (b) Hyperbola
(b) Hyperbola