样条曲面

基础概念

在建模系统中，通常使用两种类型的曲面：参数曲面和隐式曲面。参数曲面由以下函数定义：

$$\mathbf{f}(u, v) = (x(u, v), y(u, v), z(u, v))$$

其中参数 $u$ 和 $v$ 在某个特定范围内，我们假设 $u$ 和 $v$ 都在 $[0,1]$ 范围内。$(u, v)$ 是在 $uv$-坐标平面中由 $(0,0), (1,0), (0,1)$ 和 $(1,1)$ 定义的正方形中的一个点。下图说明了这个概念。

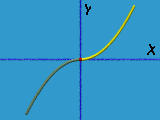
隐式曲面由三个变量的多项式定义：

$$p(x, y, z) = 0$$

与曲线类似，如果 $x(u, v)$, $y(u, v)$ 和 $z(u, v)$ 是多项式，参数曲面将无法表示 隐式曲面可以描述的许多曲面。球体是一个很好的例子。如果 $x(u, v)$, $y(u, v)$ 和 $z(u, v)$ 是有理多项式（即两个多项式的商），参数曲面可以表示球体、椭球体和许多其他曲面。然而，类似于曲线，许多隐式曲面没有任何参数形式表达。因此，在表达能力方面，隐式曲面比参数曲面更强大。

具有多项式（隐式）形式的曲面称为代数曲面。所有项的最高次数是代数曲面的次数。因此，球体和所有二次曲面都是二次代数曲面，而环面是四次代数曲面。下图显示了次数为3的代数曲面，其隐式方程为：

$$8x^2 - xy^2 + xz^2 + y^2 + z^2 - 8 = 0$$

一些代数曲面具有有理参数形式，如球体和所有二次曲面。这种类型的代数曲面称为有理代数曲面。理论上，给定一个有理参数形式的代数曲面，总是可以消除参数 $u$ 和 $v$，使结果变为隐式形式。这个过程（从参数表达到隐式表达）称为隐式化。然而，并非所有代数曲面都是有理的。而且，确定一个代数曲面是否是有理的非常困难，尽管代数几何已经提供了这样的判别定理，但是在计算上，这是比较困难的。

参数曲面

通常，许多参数曲面片并排连接在一起，形成更复杂的形状。下图显示了四个参数曲面片连接在一起形成更大的表面区域：

要计算表面上一点 $(u, v)$ 的切向量和法向量，我们需要偏导数。假设参数曲面的定义如下：

$$\mathbf{f}(u, v) = (x(u, v), y(u, v), z(u, v))$$

关于 $u$ 和 $v$ 的偏导数表示的是 $\mathbf{f}(u, v)$ 处的切向量：

$$\frac{\partial\mathbf{f}}{\partial u}=\left(\frac{\partial x}{\partial u},\frac{\partial y}{\partial u},\frac{\partial z}{\partial u}\right)\quad\mathrm{and}\quad\frac{\partial\mathbf{f}}{\partial v}=\left(\frac{\partial x}{\partial v},\frac{\partial y}{\partial v},\frac{\partial z}{\partial v}\right)$$

上式中左侧的是 $u$ 方向的切向量，而右侧的是 $v$ 方向的切向量。$\mathbf{f}(u, v)$ 处的法向量 $\mathbf{n}(u, v)$ 是这些偏导数的叉积，使用右手定则：

$$\mathbf{n}=\frac{\frac{\partial\mathbf{f}}{\partial u}\times\frac{\partial\mathbf{f}}{\partial v}}{\left|\frac{\partial\mathbf{f}}{\partial u}\times\frac{\partial\mathbf{f}}{\partial v}\right|}$$

参数曲面片可以被认为是（无限多的）曲线的集合。有许多方法可以划分出这些曲线，但是，最简单的是等参数曲线。

给定参数曲面 $\mathbf{f}(u, v)$，如果 $u$ 固定为一个值，比如说 0.1，让 $v$ 变化，这将在曲面上生成一条 $u$ 坐标为常数的曲线。这是 $u = 0.1$ 方向的等参数曲线。

类似地，固定 $v$ 到一个值并让 $u$ 变化，我们得到一个 $v$ 方向为常数的等参数曲线。因此，让 $u$ 固定在 0, 0.1, 0.2, …, 0.9 和 1，我们将有 11 条等参数曲线 $\mathbf{f}(0, v), \mathbf{f}(0.1, v), \mathbf{f}(0.2, v), ..., \mathbf{f}(0.9, v)$ 和 $\mathbf{f}(1, v)$。如果我们让 $u$ 从 0 连续变化到 1，类似地，生成的等参数曲线也会覆盖了整个曲面。下图显示了两个方向上的一些等参数曲线：

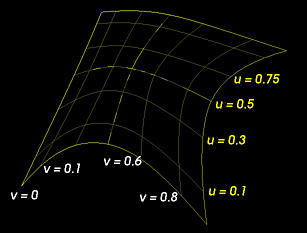
这些等参数曲线可以帮助渲染曲面。在许多应用中，参数曲面被 “三角化”（或多边化或网格化） 成三角形或多边形。然后，这些三角形和多边形可以非常高效地使用现有的图形编程库（如 OpenGL 和 PHIGS PLUS）进行渲染。

与其对曲面进行三角剖分，不如对 $(u,v)$ 参数域进行三角剖分。我们可以将 $u$ 方向细分为 $m$ 段，$u_0=0, u_1, ..., u_i, ..., u_m=1$，并将 $v$ 方向细分为 $n$ 段，$v_0=0, v_1, ..., v_j, ..., v_n=1$。域被细分为 $m \times n$ 个矩形，每个矩形可以进一步细分为两个三角形。

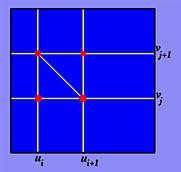
假设 $u_i$ 和 $u_{i+1}$ 是 $u$ 方向上的两个连续分割点，$v_j$ 和 $v_{j+1}$ 是 $v$ 方向上的两个连续分割点，如上图所示。我们在参数域中有一个矩形，其顶点为 $(u_i, v_j), (u_{i+1}, v_j), (u_{i+1}, v_{j+1})$ 和 $(u_i, v_{j+1})$。由于这个矩形有两个对角线，我们有两种方法划分成三角形。我们按照上图所示的方式划分。第一个三角形由 $(u_i, v_j), (u_{i+1}, v_j)$ 和 $(u_i, v_{j+1})$ 定义，第二个三角形由 $(u_{i+1}, v_j), (u_{i+1}, v_{j+1})$ 和 $(u_i, v_{j+1})$ 定义。

由 $(u_i, v_j), (u_{i+1}, v_j)$ 和 $(u_i, v_{j+1})$ 定义的三角形，这三个点分别映射到曲面上的三个点 $\mathbf{f}(u_i, v_j), \mathbf{f}(u_{i+1}, v_j)$ 和 $\mathbf{f}(u_i, v_{j+1})$，法向量为 $\mathbf{n}(u_i, v_j), \mathbf{n}(u_{i+1}, v_j)$ 和 $\mathbf{n}(u_i, v_{j+1})$。现在，我们有三个顶点，每个顶点都有一个法向量。这六个信息足以渲染出这个三角形。

因此，我们有一种方法可以渲染参数曲面。或者，换句话说，我们有一种方法可以生成一组近似给定参数曲面的三角形。这种近似可能不是一个好的近似，因为它可能有太多的三角形，其中一些三角形可能位置不正确或太小。然而，这种情况可以通过"自适应"技术来改进。自适应技术动态调整三角形的大小、数量和位置，可以很好的逼近原曲面的形状。

隐式曲面

隐式曲面在建模中非常有用。例如，假设我们给出了两个曲面，并希望找到一个可以平滑连接这两个曲面的第三个曲面。这个过程称为混合，第三个曲面是给定曲面的混合曲面。当然，这个混合曲面不是唯一的，通常以隐式形式出现。下图显示了一个混合曲面（黄色），它混合了绿色和蓝色曲面。混合曲面提供了从绿色曲面到蓝色曲面的平滑过渡。

除了混合，许多应用和计算，如偏移都会自然生成代数曲面。事实上，在许多情况下，代数曲面非常有用。点分类就是一个很好的例子。

点分类是确定给定点是位于曲面内部、上还是外部。为参数曲面设计这样的算法并不容易；然而，对于隐式曲面来说，这是一件简单的事情。假设给定点是 $(a, b, c)$，隐式曲面由 $p(x, y, z) = 0$ 给出。那么，如果 $p(a, b, c)$ 大于、等于或小于零，$(a, b, c)$ 位于曲面的外部、上还是内部。

要计算曲面的法向量，使用代数曲面的表达就很容易。多项式 $p(x, y, z) = 0$ 的形式导数向量就是它的梯度，也被称为形式梯度或形式导数向量。这个向量包含了多项式在各个变量方向上的导数信息：

$$\nabla(p)=\left(\frac{\partial p}{\partial x},\frac{\partial p}{\partial y},\frac{\partial p}{\partial z}\right)$$

一旦得到了某点的法向量，就可以很容易地计算曲面的切平面。

遗憾的是，要显示一个代数曲面并不容易。最简单但也最耗时的方法是光线追踪。许多光线追踪器允许用户指定一个隐式方程。POVRAY 和 Radiance 是很好的例子。然而，光线追踪非常慢。另一种可能性是三角化曲面，这与我们之前对参数曲面所做的类似。

然而，对于隐式曲面，情况是不同的，因为没有可以进行三角剖分的区域，因为三角化必须直接在曲面上进行。能够将隐式曲面细分为多边形（不一定是三角形）的程序通常被称为多边形生成器。开发这样的多边形生成器并不容易，仍然是一个研究问题。

下图是使用多边形生成器生成的曲面，左侧的曲面是双曲抛物面，右侧的是环形杜宾环面，这是一个四次有理曲面。这两个曲面被三角化为大量小三角形，每个三角形都使用随机颜色着色。然而实际上，并不需要这么多的三角形。

奇点

多边形生成器的一个普遍问题是，它们中的大多数并不很好地处理奇点。如果参数或隐式曲面上的一个点的所有偏导数都为零，则该点是奇点。奇点是曲面自相交或曲面上锐角的地方，下图显示了不同类型的奇点。

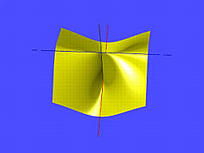
第一个是一个立方曲面，其方程为：

$x^2 + y^3 - y^2 + z^2 = 0$

这个曲面的梯度为：

$(2x, 3y^2 - 2y, 2z)$

因此，$(0,0,0)$ 是一个奇点，因为在这一点上梯度的所有分量都为零，$(0, 2/3, 0)$ 处是另一个奇点。

中间的图形的方程如下：

$-x^3 + 2xz - yz^2 = 0$

这个曲面的梯度向量为：

$(-2x^2 + 2z, -2yz, 2x - y^2)$

若要求奇点，则每个分量都必须是0，根据第二个分量，我们有 $y = 0$ 或 $z = 0$。如果 $y = 0$，第三个分量要求 $x$ 为零，第一个分量要求 $z$ 为零。如果 $z = 0$，第一个分量要求 $x$ 为零，第三个分量要求 $x$ 为零。这两种情况得到的奇点都为 $(0,0,0)$。

前两种情况只有孤立的奇点，而奇点页可以在一条直线上，甚至可以在一条曲线上。我们看上面的右图，其方程为：

$-x^2y + x^2 - yz^2 - z^2 = 0$

曲面的梯度向量为：

$(-2xy + 2x, -(x^2 + z^2), -2z)$

如果 $z = 0$，根据第二个分量，意味着 $x$ 也必须为零。如果 $x$ 和 $z$ 都为零，第一个分量也将为零，不管 $y$ 可能有什么值。意味着只要 $x = z = 0$ 且 $y$ 有任意值，则该点就是奇点。因此，$y$ 轴包含所有奇点。图中画出了三条线。它们都位于曲面上；垂直的那条线是 $y$ 轴，即包含所有奇点的自交线。

构造贝塞尔(Bézier)曲面

贝塞尔曲面由一组二维的控制点集 $\mathbf{p}_{i,j}$ 定义，其中 $i$ 的范围是 0 到 $m$，$j$ 的范围是 0 到 $n$。因此，在这种情况下，我们有 $m + 1$ 行、$n + 1$ 列控制点，$\mathbf{p}_{i,j}$ 表示第 $i$ 行第 $j$ 列的控制点。我们总共有 $(m + 1)(n + 1)$ 个控制点。

以下是 $m + 1$ 行 $n + 1$ 列控制点定义的贝塞尔曲面的方程：

$$p(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} B_{m,i}(u) B_{n,j}(v)\mathbf{p}_{i,j}$$

其中 $B_{m,i}(u)$ 和 $B_{n,j}(v)$ 分别是 $u$ 方向和 $v$ 方向的第 $i$ 个和第 $j$ 个贝塞尔基函数。这些基函数定义如下：

$$B_{m,i}(u) = \frac{m!}{i!(m-i)!} u^i (1-u)^{m-i} \\ B_{n,j}(v) = \frac{n!}{j!(n-j)!} v^j (1-v)^{n-j}$$

由于 $B_{m,i}(u)$ 和 $B_{n,j}(v)$ 是 $m$ 阶和 $n$ 阶的函数，我们可以说这是一个 $(m,n)$ 阶的贝塞尔曲面。控制点集通常被称为 贝塞尔网或控制网。参数 $u$ 和 $v$ 在 0 到 1 的范围内，因此贝塞尔曲面将参数域上的单位正方形映射到空间中的一个矩形曲面片。

下图显示了一个由 3 行 3 列（9 个）控制点定义的贝塞尔曲面，因此是一个阶数为（2,2）的贝塞尔曲面。

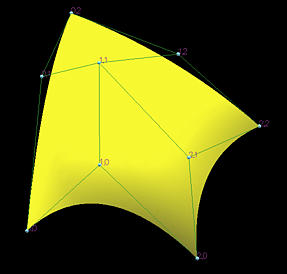
基函数

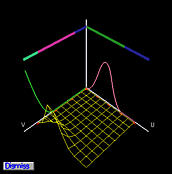
贝塞尔曲面的基函数是控制点的系数。从定义中可以清楚地看出，这些二维基函数是两个一维贝塞尔基函数的乘积，因此贝塞尔曲面的基函数是定义在单位正方形上的两个变量 $u$ 和 $v$ 的参数曲面。

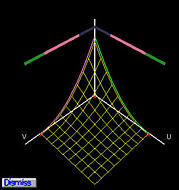
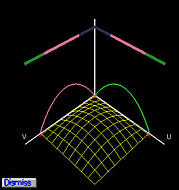
下图显示了控制点 $\mathbf{p}_{0,0}$（左）和 $\mathbf{p}_{1,1}$（右）的基函数。对于控制点 $\mathbf{p}_{0,0}$，其基函数是 $u$ 方向上的一维贝塞尔基函数 $B_{2,0}(u)$ 和 $v$ 方向上的 $B_{2,0}(v)$ 的乘积。在左图中，$B_{2,0}(u)$ 和 $B_{2,0}(v)$ 以及它们的乘积（以线框图显示）都显示出来了。右图显示了 $\mathbf{p}_{1,1}$ 的基函数，它是 $u$ 方向上的 $B_{2,1}(u)$ 和 $v$ 方向上的 $B_{2,1}(v)$ 的乘积。

张量积曲面

张量积通过两条曲线"相乘"来构造曲面。给定两条贝塞尔、B样条或NURBS曲线，张量积方法通过将第一条曲线的基函数与第二条曲线的基函数相乘，并将结果作为一组二维控制点的基函数来构造曲面。以这种方式生成的曲面称为张量积曲面。因此，贝塞尔曲面、B样条曲面和NURBS曲面都是张量积曲面。

贝塞尔曲面的重要性质

这里列出了几个贝塞尔曲面的重要性质。这些性质可以通过与贝塞尔曲线类似的方式证明。可以将这些重要性质与贝塞尔曲线的性质进行比较。

贝塞尔曲面的方程：

$$p(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} B_{m,i}(u) B_{n,j}(v) p_{i,j}$$

其中两个一维基函数定义如下：

$$B_{m,i}(u)=\frac{m!}{i!(m-i)!}u^i(1-u)^{m-i} \\ B_{n,j}(v)=\frac{n!}{j!(n-j)!}v^j(1-v)^{n-j}$$

性质

• $p(u, v)$ 经过控制网格四个角上的控制点：$p_{0,0}$, $p_{m,0}$, $p_{m,n}$ 和 $p_{0,n}$

  我们有 $p(0,0) = p_{0,0}$, $p(1,0) = p_{m,0}$, $p(0,1) = p_{0,n}$ 和 $p(1,1) = p_{m,n}$。

• 非负性： 对于所有的 $m, n, i, j$ 和 $u$ 和 $v$（取值范围为$[0,1]$），$B_{m,i}(u)$ 和 $B_{n,j}(v)$ 都是非负的

• 单位分割（Partition of Unity）： 对于$[0,1]$范围内的所有 $u$ 和 $v$，$B_{m,i}(u) B_{n,j}(v)$ 的和是1。

  当$u$和$v$位于$[0,1]$时，以下条件成立：

  $\sum_{i=0}^{m} \sum_{j=0}^{n} B_{m,i}(u) B_{n,j}(v) = 1$

• 凸包性质： 贝塞尔曲面 $p(u, v)$ 位于由其控制网格定义的凸包内。

  由于 $p(u, v)$ 是所有控制点的线性组合，并且系数之和为 1，因此曲面位于其控制点的凸包内。

• 仿射不变性： 这意味着对贝塞尔曲面应用仿射变换，可以通过对所有控制点应用变换来实现，并且由变换后的控制点定义的曲面与将变换应用到曲面方程得到的新曲面是相同的。

• 变差减少性质： 对于曲面来说，没有这样的性质。

等参数曲线

参数曲面的定义为：

$$\mathbf{f}(u, v) = (x(u, v), y(u, v), z(u, v))$$

固定参数 $u$ 为 $a$ 时，等参数曲线的定义为 $\mathbf{f}(a, v)$。这个函数只有一个变量 $v$，因此表示 $v$ 方向上的一条曲线。类似地，固定 $v$ 为 $b$ 的等参数曲线为 $\mathbf{f}(u, b)$。

贝塞尔曲面上的等参数曲线具有非常简单的结构，实际上在任何张量积曲面上的等参数曲线也是如此。在贝塞尔曲面的方程中，基函数 $B_{m,i}(u)$ 仅依赖于索引 $i$ 并且可以独立出来，如下：

$$\mathbf{p}(u,v)=\sum_{i=0}^mB_{m,i}(u)\left(\sum_{j=0}^nB_{n,j}(v)\mathbf{p}_{i,j}\right)$$

括号内的表达式为基函数 $B_{n,j}(v)$ 和控制点 $p_{i,j}$ 的乘积，虽然基函数不依赖于 $i$；但控制点依赖于$i$的取值。因此，我们可以定义一个新的函数 $q_i(v)$ 来简化一下：

$$q_i(v) = \sum_{j=0}^{n}B_{n,j}(v) p_{i,j}$$

显然，每个 $q_i(v)$ 是由控制点 $p_{i,0}, p_{i,1}, \ldots, p_{i,n}$ 定义的贝塞尔曲线（即第 $i$ 行控制点）。因此，我们有 $m + 1$ 个新的点 $q_0(v), q_1(v), \ldots, q_m(v)$。由于 $v$ 是固定的，可以视为常数，点 $q_0(v), q_1(v), \ldots, q_m(v)$ 不会随着 $u$ 的变化而改变位置。因此，曲面方程变为：

$$p(u, v) = \sum_{i=0}^{m} B_{m,i}(u) q_i(v)$$

由于 $v$ 是固定的，$p(u, v)$ 实际上是一个关于$u$的单变量参数方程，因此 $p(u, v)$ 表示曲面上的一条曲线。这是一条由 $m + 1$ 个控制点 $q_0(v), q_1(v), \ldots, q_m(v)$ 定义的 $u$ 方向的贝塞尔曲线。

因此，我们得出结论：固定参数 $v$ 得到的等参数曲线是由一组控制点定义的贝塞尔曲线，这些控制点可以从曲面方程计算得出。 若固定参数$u$，可以得出相同的结论。以下显示了贝塞尔曲面上两个方向上等参数曲线的图：

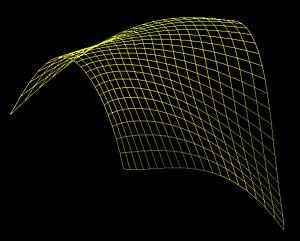
边界曲线

有四个特殊的等参数曲线：$p(0, v), p(1, v), p(u, 0)$ 和 $p(u, 1)$。这些是边界曲线（曲面片段的边界），因为它们将参数域上单位正方形的边界映射到曲面上。将 $u$ 设置为 0 和 1，将 $v$ 设置为 0 和 1，可以得到边界曲线的方程：

$$\begin{gathered} \mathbf{p}(0,v) =\sum_{j=0}^{n}B_{n,j}(v)\mathbf{p}_{0,j} \\ \mathbf{p}(1,v) =\sum_{j=0}^nB_{n,j}(v)\mathbf{p}_{m,j} \\ \mathbf{p}(u,0) =\sum_{i=0}^mB_{m,i}(u)\mathbf{p}_{i,0} \\ \mathbf{p}(u,1) =\sum_{i=0}^mB_{m,i}(u)\mathbf{p}_{i,n} \end{gathered}$$

因此，$u = 0$ 和 $u = 1$ 对应的边界曲线是由第 $0$ 行和第 $m$ 行控制点定义的贝塞尔曲线。类似地，$v = 0$ 和 $v = 1$ 对应的边界曲线是由第 $0$ 列和第 $n$ 列控制点定义的贝塞尔曲线。

$u$ 方向和 $v$ 方向

我们知道控制点的数量被分为 $m + 1$ 行 $n + 1$ 列，那么行、列与 $u$、$v$ 方向之间的关系是什么？回想一下，$v$ 方向表示的是当 $u$ 固定为常数时的参数曲线。在这种情况下，控制点的定义可以重写成如下形式：

$$\mathbf{p}(u,v)=\sum_{i=0}^mB_{m,i}(u)\left(\sum_{j=0}^nB_{n,j}(v)\mathbf{p}_{i,j}\right)$$

因此，随着 $v$ 的变化，括号内的表达式表示的是由控制点 $p_{i,0}, p_{i,1}, \ldots, p_{i,n}$ 定义的贝塞尔曲线，这些是第 $i$ 行的控制点。

因此，$v$ 方向的曲线沿水平变化，类似的我们可以知道 $u$ 方向的曲线是沿着竖直方向变化的。

例如，边界曲线 $p(0, v)$ 和 $p(1, v)$ 在 $v$ 方向上，分别由第 0 行和第 $n$ 行控制点定义；边界曲线 $p(u, 0)$ 和 $p(u, 1)$ 在 $u$ 方向上，分别由第 0 列和第 $m$ 列控制点定义。

张量积曲面再探

现在研究一下张量积的实际含义。让我们回到上面的方程。如果我们将控制点排列成一个 $m + 1$ 行 $n + 1$ 列的矩阵：

$$\left.\left[\begin{array}{cccc}\mathbf{p}_{0,0}&\mathbf{p}_{0,1}&\cdots&\mathbf{p}_{0,n}\\\mathbf{p}_{1,0}&\mathbf{p}_{1,1}&\cdots&\mathbf{p}_{1,n}\\\vdots&&\ddots&\vdots\\\mathbf{p}_{m,0}&\mathbf{p}_{m,1}&\cdots&\mathbf{p}_{m,n}\end{array}\right.\right]$$

并将 $v$ 方向贝塞尔曲线的基函数排列成一个 $n + 1$ 行的列矩阵：

$$\left.\left[\begin{array}{c}B_{n,0}(v)\\B_{n,1}(v)\\\vdots\\B_{n,n}(v)\end{array}\right.\right]$$

那么括号内的结果$\left(\sum_{j=0}^nB_{n,j}(v)\mathbf{p}_{i,j}\right)$可以重写为一个矩阵乘积：

$$\left.\left[\begin{array}{cccc}\mathbf{p}_{0,0}&\mathbf{p}_{0,1}&\cdots&\mathbf{p}_{0,n}\\\mathbf{p}_{1,0}&\mathbf{p}_{1,1}&\cdots&\mathbf{p}_{1,n}\\\vdots&&\ddots&\vdots\\\mathbf{p}_{m,0}&\mathbf{p}_{m,1}&\cdots&\mathbf{p}_{m,n}\end{array}\right.\right].\left[\begin{array}{c}B_{n,0}(v)\\B_{n,1}(v)\\\vdots\\B_{n,n}(v)\end{array}\right]$$

如果我们将 $u$ 方向的贝塞尔曲线基函数写成一个 $m + 1$ 行的行矩阵，那么结果就是有 $m + 1$ 个元素的列矩阵：

$$[B_{m,0}(u),B_{m,1}(u),\cdots,B_{m,m}(u)]$$

因此，贝塞尔曲线的方程就变成了三个矩阵的乘积，如下所示：

$$\left.\mathbf{p}(u,v)=\left[B_{m,0}(u),B_{m,1}(u),\cdots,B_{m,m}(u)\right]\cdot\left[\begin{array}{cccc}\mathbf{p}_{0,0}&\mathbf{p}_{0,1}&\cdots&\mathbf{p}_{0,n}\\\mathbf{p}_{1,0}&\mathbf{p}_{1,1}&\cdots&\mathbf{p}_{1,n}\\\vdots&&\ddots&\vdots\\\mathbf{p}_{m,0}&\mathbf{p}_{m,1}&\cdots&\mathbf{p}_{m,n}\end{array}\right.\right]\cdot\left[\begin{array}{c}B_{n,0}(v)\\B_{n,1}(v)\\\vdots\\B_{n,n}(v)\end{array}\right]$$

因此，我们将贝塞尔曲面的定义转换为矩阵乘积形式。由于控制点矩阵中的每个元素也是一个矩阵（即，每个控制点可以被认为是一个向量，因此可以视为一个矩阵），这是数学中的张量积形式。因此，贝塞尔曲面是张量积曲面。

贝塞尔曲面：de Casteljau算法

可以对 De Casteljau 算法扩展以处理贝塞尔曲面。准确地说，当给定 $(u, v)$ 时，可以使用De Casteljau 算法来找到贝塞尔曲面 $\mathbf{p}(u, v)$ 上对应的点。下面将基于前面提到的等参数曲线的概念进行讨论。

回想一下贝塞尔曲面的方程：

$$p(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} B_{m,i}(u) B_{n,j}(v)\mathbf{p}_{i,j}$$

可以重写为以下形式：

$$\mathbf{p}(u,v)=\sum_{i=0}^mB_{m,i}(u)\left(\sum_{j=0}^nB_{n,j}(v)\mathbf{p}_{i,j}\right)$$

对于 $i = 0, 1, \ldots, m$，$\mathbf{q}_i(v)$ 的定义如下：

$$\mathbf{q}_i(v) = \sum_{j=0}^{n} B_{n,j}(v) \mathbf{p}_{i,j}$$

对于固定的 $v$ 值，我们有 $m + 1$ 个点 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$。每个 $\mathbf{q}_i(v)$ 是由控制点 $\mathbf{p}_{i,0}, \mathbf{p}_{i,1}, \ldots, \mathbf{p}_{i,n}$ 定义的贝塞尔曲线上的一个点。将上式代回曲面方程可以简化成：

$$\mathbf{p}(u,v)=\sum_{i=0}^mB_{m,i}(u)\mathbf{q}_i(v)$$

这意味着 $\mathbf{p}(u, v)$ 是由 $m + 1$ 个控制点 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$ 定义的贝塞尔曲线上的一个点。因此，我们得出以下结论：

要在贝塞尔曲面上找到点 $\mathbf{p}(u, v)$，我们可以找到 $m + 1$ 个点 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$，然后根据这些控制点可以计算得出 $\mathbf{p}(u, v)$。

这个结论为我们计算 $\mathbf{p}(u, v)$ 提供了一个简单的方法。因为每个点 $\mathbf{q}_i(v)$ 是由第 $i$ 行控制点：$\mathbf{p}_{i,0}, \mathbf{p}_{i,1}, \ldots, \mathbf{p}_{i,n}$ 定义的贝塞尔曲线上的一个点：对于第 $i$ 行控制点（$v$值已知），我们可以对贝塞尔曲线应用 De Casteljau 算法来计算 $\mathbf{q}_i(v)$。对 $m + 1$ 行都使用 De Casteljau 算法之后（即，每行一次），我们就得到了 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$。然后，再对这 $m + 1$ 个控制点应用 De Casteljau 算法（$u$值已知），最终可以得到曲面上的点 $\mathbf{p}(u, v)$！

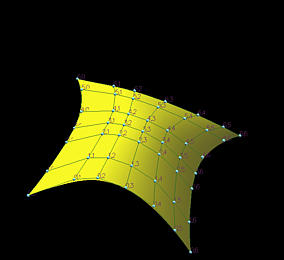
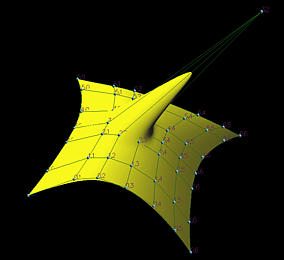
下图说明了这个概念。给定的曲面是一个由 3x3 控制网定义的二阶（2,2）贝塞尔曲面。假设 $u = \frac{2}{3}$ 和 $v = \frac{1}{3}$。为了求 $\mathbf{q}_0(\frac{1}{3})$，我们取第 0 行的控制点 $\mathbf{p}_{0,0}, \mathbf{p}_{0,1}$ 和 $\mathbf{p}_{0,2}$，$v = \frac{1}{3}$，对这个贝塞尔曲线应用 De Casteljau 算法。对第一行和第二行重复这个过程（第一行和第二行都满足 $v = \frac{1}{3}$）。这产生了三个中间控制点 $\mathbf{q}_0(\frac{1}{3}), \mathbf{q}_1(\frac{1}{3})$ 和 $\mathbf{q}_2(\frac{1}{3})$。最后，对这三个新的控制点应用 De Casteljau 算法（$u = \frac{2}{3}$ 已知）。结果是 $\mathbf{p}(\frac{2}{3},\frac{1}{3})$，图中用黄色显示。

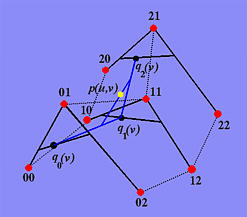
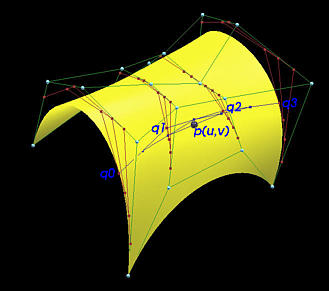
下面显示的是给定贝塞尔曲面的示例。控制点显示为白色。该曲面控制网有四行五列，因此是一个阶数为 (3,4) 的贝塞尔曲面。对于每一行，首先会在红色线段上计算出一些中间控制点， 图中显示了四个中间控制点 $\mathbf{q}_0, \mathbf{q}_1, \mathbf{q}_2$ 和 $\mathbf{q}_3$，蓝色多段线表示由中间控制点 $\mathbf{q}_0, \mathbf{q}_1, \mathbf{q}_2$ 和 $\mathbf{q}_3$ 连成的控制多段线，在这个曲面上的最终点 $\mathbf{p}(u,v)$ 以黑色球体显示。

最后，下面是对这个算法的总结：

Input：$m + 1$ 行和 $n + 1$ 列的控制点和 $(u, v)$。
Output：曲面上的点 $\mathbf{p}(u, v)$。
for $i = 0$ to $m$ do：
begin
对第 $i$ 行控制点应用 De Casteljau 算法（$v$已知）；
设得到的点为 $\mathbf{q}_i(v)$；
end
对 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$ 应用 De Casteljau 算法（$u$ 已知）；
得到的点是 $\mathbf{p}(u, v)$。

B样条曲面：构造

给定以下信息：

1. 一组 $m + 1$ 行 $n + 1$ 列的控制点 $\mathbf{p}_{i,j}$，其中 $0 \leq i \leq m$，$0 \leq j \leq n$；

2. $u$ 方向上有 $h + 1$ 个节点，节点向量 $U = \{ u_0, u_1, \ldots, u_h \}$；

3. $v$ 方向上有 $k + 1$ 个节点，节点向量 $V = \{ v_0, v_1, \ldots, v_k \}$；

4. $u$ 方向的阶数为 $p$

5. $v$ 方向的阶数为 $q$

根据这些信息定义的 B 样条曲面如下：

$$p(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,p}(u) N_{j,q}(v) \mathbf{p}_{i,j}$$

其中 $N_{i,p}(u)$ 和 $N_{j,q}(v)$ 分别是 $u$ 方向和 $v$ 方向的 B 样条基函数，次数分别为 $p$ 和 $q$。注意，B样条曲面必须满足基本恒等式，即：$h = m + p + 1$ 和 $k = n + q + 1$。

B 样条曲面是张量积曲面的另一个例子。与贝塞尔曲面一样，控制点集通常称为控制网，$u$ 和 $v$ 的范围是 0 到 1。因此，B 样条曲面是将参数空间中的单位正方形映射到一个空间中的矩形曲面片上。

下图显示了一个由 6 行 6 列控制点定义的 B 样条曲面：

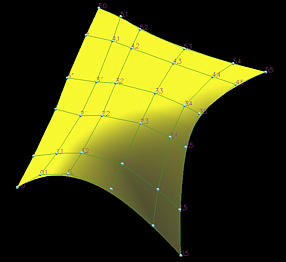
$u$ 方向的节点向量为 $U = \{ 0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1 \}$，阶数为 2。$v$ 方向的节点向量为 $V = \{ 0, 0, 0, 0, 0.33, 0.66, 1, 1, 1, 1 \}$，阶数为 3。

基函数

控制点 $\mathbf{p}_{i,j}$ 的系数是 $u$ 方向的一维 B 样条基函数 $N_{i,p}(u)$ 和 $v$ 方向的一维 B 样条基函数 $N_{j,q}(v)$ 的乘积，这些乘积都是二维 B 样条函数。下图显示了控制点 $\mathbf{p}_{2,0}, \mathbf{p}_{2,1}, \mathbf{p}_{2,2}, \mathbf{p}_{2,3}, \mathbf{p}_{2,4}$ 和 $\mathbf{p}_{2,5}$ 的基函数。

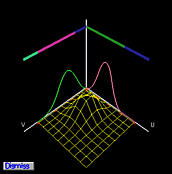
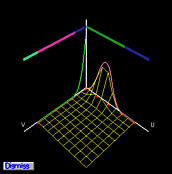
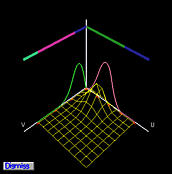
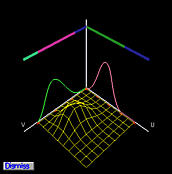
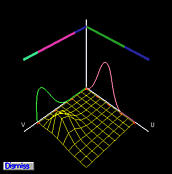
二维基函数显示为线框曲面。由于控制点在同一行上，$u$ 方向的基函数是固定的，而 $v$ 方向的基函数会变化。由于 B 样条基函数通常只在几个连续的节点区间上非零（局部修改特性），因此至少存在一个节点区间，使得两个一维B样条基函数都不为0，因此它们的乘积，即二维B样条基函数不为零

Clamped、Closed和Open B 样条曲面

B 样条曲线有三种类型，可以是Clamped、Closed或Open的，因此B 样条曲面也可以在每个方向上具有三种类型。

也就是说，我们让 B 样条曲面在 $u$ 方向上是Clamped的，在 $v$ 方向上是Closed。如果一个 B 样条在两个方向上都是Clamped，那么这个曲面就会通过控制点 $\mathbf{p}_{0,0}, \mathbf{p}_{m,0}, \mathbf{p}_{0,n}$ 和 $\mathbf{p}_{m,n}$ 并且在这四个控制点处与控制网的八个边相切。

如果一个 B 样条曲面在某个方向上是Closed的，那么这个方向上的所有等参数曲线都是Closed曲线，并且曲面会变成管状。

如果一个 B 样条曲面在两个方向上都是Open的，那么曲面就不会通过控制点 $\mathbf{p}_{0,0}, \mathbf{p}_{m,0}, \mathbf{p}_{0,n}$ 和 $\mathbf{p}_{m,n}$。我们只讨论在两个方向上都是Clamped的 B 样条曲面。

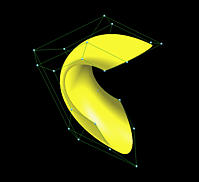
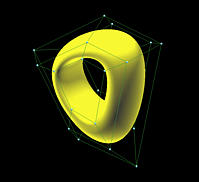
下图显示了在两个方向上Clamped、Closed和Open的三个B 样条曲面。这三个曲面都同一组控制点定义，但是它们的节点向量不同，因为他们在$u$方向和$v$方向的曲线类型是不相同的。

B 样条曲面的重要性质

这里列出了几个 B 样条曲面的重要性质。这些性质可以通过应用与B样条曲线中类似的方式证明

B 样条曲面的方程：

$$p(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,p}(u) N_{j,q}(v)\mathbf{p}_{i,j}$$

其中 $u$ 方向和 $v$ 方向的次数分别为 $p$ 和 $q$，有 $m + 1$ 行 $n + 1$ 列个控制点。

• 非负性： 对于所有的 $p, q, i, j$ 以及 $0\le u \le1$ 和 $0\le v \le 1$，$N_{i,p}(u)$ 和 $N_{j,q}(v)$ 是非负的。

• 单位分割（Partition of Unity）： 对所有 $0\le u \le1$ 和 $0\le v \le 1$ 内的取值，$N_{i,p}(u) N_{j,q}(v)$ 和为 1。

  准确地说，以下等式成立，其中 $0\le u \le1$ 和 $0\le v \le 1$：

  $$\sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,p}(u) N_{j,q}(v) = 1$$

• 强凸包性质（Strong Convex Hull Property）： 如果 $(u, v)$ 在 $[u_i, u_{i+1}) \times [v_j, v_{j+1})$ 内，则 $p(u, v)$ 位于由控制点 $\mathbf{p}_{h,k}$ 定义的凸包内，其中 $i-p \leq h \leq i$ 和 $j-q \leq k \leq j$。

  B 样条曲面的这种强凸包性质源于B样条曲线的强凸包性质。对于 $u$ 方向，如果 $u$ 在 $[u_i, u_{i+1})$ 内，那么最多有 $p+1$ 个非零基函数，即 $N_{i,p}(u), N_{i-1,p}(u), \ldots, N_{i-p,p}(u)$。因此，只有在 $i-p$ 到 $i$ 行的控制点在 $u$ 方向上有非零基函数。类似地，如果 $v$ 在 $[v_j, v_{j+1})$ 内，那么在这个结区间上最多有 $q+1$ 个非零基函数，即 $N_{j,q}(v), N_{j-1,q}(v), \ldots, N_{j-q,q}(v)$。因此，只有在 $j-q$ 到 $j$ 列的控制点在 $v$ 方向上有非零基函数。综合这两点，只有在 $i-p$ 到 $i$ 行，$j-q$ 到 $j$ 列的控制点有非零基函数，这些基函数是非负的，并且它们的和是一，因此，$p(u, v)$ 位于由这些控制点定义的凸包内。

  因此，定义在 $[u_i, u_{i+1}) \times [v_j, v_{j+1})$ 上的曲面片位于凸包内。

• 局部修改特性（Local Modification Scheme）：

  如果 $(u, v)$ 在区域 $[u_i, u_{i+p+1}) \times [v_j, v_{j+q+1})$ 外，那么 $N_{i,p}(u) N_{j,q}(v)$ 是零。

  根据局部修改特性我们知道，在 $u$ 方向上，$N_{i,p}(u)$ 在 $[u_i, u_{i+p+1})$ 上非零，并且在其他区间值为零。B 样条曲面的局部修改特性也继承于B样条曲线。下图中，如果控制点 $\mathbf{p}_{3,2}$ 移动到一个新位置，只有移动的控制点上的邻近区域改变形状，其他地方保持不变。

  

• 如果 $u$ 是重数为 $s$ 的节点，那么 $p(u, v)$ 在 $u$ 方向上是 $C^{p-s}$ 连续的，如果 $v$ 是重数为 $t$ 的节点，那么 $p(u, v)$ 在 $v$ 方向上是 $C^{q-t}$ 连续的。

• 仿射不变性（Affine Invariance）： 这意味着对 B 样条曲面应用仿射变换，可以通过对所有控制点应用变换来实现，并且由变换后的控制点定义的曲面与通过应用相同变换到曲面方程得到的曲面是相同的。

• 变差减少性质（Variation Diminishing Property）： 对于曲面来说，没有这样的性质。

• 如果 $m = p$, $n = q$，并且 $U = \{ 0, 0, ..., 0, 1, 1, ...., 1 \}$，那么 B 样条曲面就退化成贝塞尔曲面。

B-样条曲面: de Boor算法

前面我们提到了用 De Casteljau 算法计算贝塞尔曲面上一点，同样的，de Boor 算法也可以用于计算B样条曲面和 NURBS 曲面上一点。实际上，由于B样条曲面具有局部修改性质，de Boor 算法看起来非常类似于 De Casteljau 算法。将B样条曲面的方程写成如下形式：

$$\mathbf{p}(u,v)=\sum_{i=0}^{m}N_{i,p}(u)\left(\sum_{j=0}^{n}N_{j,q}(v)\mathbf{p}_{i,j}\right)$$

对于固定的 $i$ 值，括号内的曲线就是由第 $i$ 行控制点定义的 B 样条曲线。我们定义 $\mathbf{q}_i(v)$ 如下：

$$\mathbf{q}_i(v) = \sum_{j=0}^{n} N_{j,q}(v)\mathbf{p}_{i,j}$$

因此，$\mathbf{q}_i(v)$ 是由第 $i$ 行控制点定义的 B 样条曲线上的一个点。

如果 $v$ 在区间 $[v_d, v_{d+1})$ 内，那么在计算 $\mathbf{q}_i(v)$ 时，只涉及 $q+1$ 个控制点，其中 $q$ 是 $N_{j,q}(v)$ 的次数。
如果 $v$ 不等于 $v_d$，这些控制点是 $\mathbf{p}_{i,d}, \mathbf{p}_{i,d-1}, \ldots, \mathbf{p}_{i,d-q}$。
如果 $v$ 等于 $v_d$，一个重数为 $t$ 的节点，那么控制点是 $\mathbf{p}_{i,d-t}, \mathbf{p}_{i,d-t-1}, \ldots, \mathbf{p}_{i,d-q}$。

因此，从 $d-q$ 到 $d-t$ 列的控制点，如果 $v$ 值不等于节点值，那么重数 $t$ 是零，我们可以对每一行应用 de Boor 算法，得到 $m + 1$ 个新的点 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$，如下图所示：

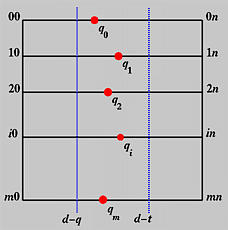
将这些新点重新代入曲面方程，我们有：

$$\mathbf{p}(u, v) = \sum_{i=0}^{m} N_{i,p}(u) \mathbf{q}_i(v)$$

因此，$\mathbf{p}(u, v)$ 是由 $\mathbf{q}_0(v), \mathbf{q}_1(v), \ldots, \mathbf{q}_m(v)$ 定义的 B 样条曲线上的一个点。因此，要找到 $\mathbf{p}(u, v)$，我们需要找到这个曲线上对应于 $u$ 处的点。可以再次使用de Boor 算法计算得到。

设 $u$ 在节点区间 $[u_c, u_{c+1})$ 内。根据局部修改性质，只有 $p+1$ 个控制点参与计算，其中 $p$ 是 B 样条曲线的次数。如果 $u$ 不等于 $u_c$，控制点是 $\mathbf{q}_c(v), \mathbf{q}_{c-1}(v), \ldots, \mathbf{q}_{c-p}(v)$。如果 $u$ 等于 $u_c$，则 $u$ 是重数为 $s$ 的节点，控制点是 $\mathbf{q}_{c-s}(v), \mathbf{q}_{c-s-1}(v), \ldots, \mathbf{q}_{c-p}(v)$。

因此，尽管每一行控制点都可以产生一个 $\mathbf{q}_i(v)$，但并非所有行都是必需的，根据局部修改性质，只需要 $p+1$ 行。如下图所示：

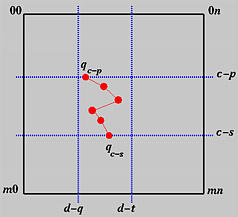
总之，给定 $u$ 在 $[u_c, u_{c+1})$ 内和 $v$ 在 $[v_d, v_{d+1})$ 内，对于 $c-p$ 和 $c-s$ 范围内的第 $i$ 行，对控制点 $\mathbf{p}_{i,d-q}, \mathbf{p}_{i,d-q+1}, \ldots, \mathbf{p}_{i,d-t}$ 使用 de Boor 算法得到一个新的点 $\mathbf{q}_i(v)$。然后，对控制点 $\mathbf{q}_{c-p}(v), \mathbf{q}_{c-p+1}(v), \ldots, \mathbf{q}_{c-s}(v)$ 使用 de Boor 算法计算得到 $\mathbf{p}(u, v)$

算法总结：

Input：一组 $m + 1$ 行 $n + 1$ 列控制点，$u$ 方向和 $v$ 方向的节点向量，以及 $(u, v)$ 值。
**Output：**曲面上的点 $\mathbf{p}(u, v)$。
算法：
$u \in [u_c, u_{c+1})$；
$v \in [v_d, v_{d+1})$；
如果 $u \neq u_c$，让 $s$ 为零；否则，让 $s$ 为 $u_c$ 的重数；
如果 $v \neq v_d$，让 $t$ 为零；否则，让 $t$ 为 $v_d$ 的重数；
for $i = c-p$ to $c-s$ do：
begin:
应用 de Boor 算法，控制点为 $\mathbf{p}_{i,d-q}, \mathbf{p}_{i,d-q+1}, \ldots, \mathbf{p}_{i,d-t}$，$v$ 值给定；
结果为 $\mathbf{q}_i(v)$；
end
应用 de Boor 算法，控制点为 $\mathbf{q}_{c-p}(v), \mathbf{q}_{c-p+1}(v), \ldots, \mathbf{q}_{c-s}(v)$，$u$ 值给定；
结果为 $\mathbf{p}(u, v)$。

下图显示了一个例子。B 样条曲面由 $5 \times 5$ 个控制点和节点向量（$u$方向和$v$方向都是）$\{0, 0, 0, 0, 0.5, 1, 1, 1, 1\}$ 定义。因此，两个方向的次数都是 3。

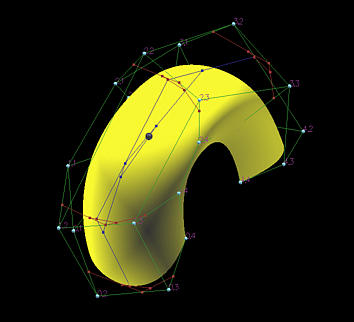
在图中，$u$ 和 $v$ 都不是节点，$u$ 小于 0.5，而 $v$ 大于 0.5。对于 $v$，由于它在 $[0.5, 1)$ 内，因此只有控制点 $\mathbf{p}_{i,1}, \mathbf{p}_{i,2}, \mathbf{p}_{i,3}$ 和 $\mathbf{p}_{i,4}$ 参与 de Boor 算法的计算。由于 $u$ 在 $[0,0.5)$ 内，在 $u$ 方向上，只使用了第 0 行、第 1 行、第 2 行和第 3 行控制点进行计算。在图中，红色折线用于计算点 $\mathbf{q}_i(v)$，而唯一的蓝色多段线用于计算曲面上的点（黑色球体）。