实体表示法
实体的表示方法
实体可以非常简单,比如一个立方体,也可以非常复杂,比如活塞发动机。要能够被计算机处理,实体必须具有可以描述几何特征的表示。
一个好的表示法应该解决以下问题:
-
域:
虽然没有一种表示能够描述所有可能的实体,但一种表示应该能够表示某一类的几何对象。 -
明确性:
当你看到一个实体的表示时,你会毫无疑问地知道被表示的是什么。一个明确的表示方法通常被称为完整的表示。 -
独特性:
换句话说,表示特定实体的方法是唯一的。如果表示是唯一的,那么很容易确定两个实体是否相同,因为可以直接比较它们的表示。 -
准确性:
如果表示几何体不需要任何近似,那么一个表示被称为精确的, -
有效性:
这意味着一个表示不应该创造任何无效或不可能的实体。 -
封闭性 :
封闭性是指对有效实体进行变换后,仍然会得到一个有效实体。 -
紧凑性和高效 :
一个好的表示方法应该足够紧凑,以节省空间,并且可以使用高效的算法来确定所需的物理特性。
这些问题可能彼此矛盾。
例如,为了提高效率,可以用多面体来逼近曲线实体。处理多面体有许多高效稳健的算法,然而,在近似过程中可能无法保持精确度。
例如,给定两个相切的曲线实体,在转换为多面体之后,这种相切关系可能消失。
即使是多面体也会出现问题,许多图形API,如PHIGS PLUS和OpenGL,都有用于表示多面体的数据结构;但是,这些表示可能会生成无效的实体。有一些表示法可以始终表示有效的实体,但是,这些表示法通常比图形API中的表示方法更复杂。
本文仅讨论以下几种表示方法:线框表示、边界表示 和 构造实体几何(CSG)。
1. 线框模型
线框模型是传统的表示实体的方式。线框模型由两个表组成,即顶点表和边表。顶点表中每行都记录了一个顶点及其坐标值,而边表中每行为该边的两个相邻顶点。线框模式没有面信息。例如,要表示由8个顶点和12条边组成的立方体,需要如下信息:
顶点表:
| Vertex | x | y | z |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 |
| 5 | 1 | 0 | 0 |
| 6 | 1 | 0 | 1 |
| 7 | 1 | 1 | 0 |
| 8 | 1 | 1 | 1 |
边表:
| Edge | Vertex 1 | Vertex 2 |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 1 | 3 |
| 3 | 1 | 5 |
| 4 | 2 | 4 |
| 5 | 2 | 6 |
| 6 | 3 | 4 |
| 7 | 3 | 7 |
| 8 | 4 | 8 |
| 9 | 5 | 6 |
| 10 | 5 | 7 |
| 11 | 6 | 8 |
| 12 | 7 | 8 |
下图展示了所有 8 个顶点和 12 条边,分别用白色和黄色表示,并用数字标识。
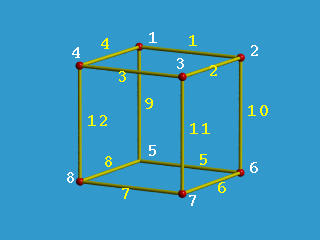
线框模型存在歧义
虽然线框模型使用了最简单的数据结构,但是它存在歧义。下面是一个例子,包含16个顶点和32条边。我们知道这代表了一个立体,并且每个四边形(其中一些是正方形)定义了这个立体的一个面。

内部立方体代表一个洞;但是,我们无法判断立方体的开口方向。如下图所示,有三种可能性。另外两种可以通过旋转第三种立体表示得到。

因为线框模型存在歧义,它的用途受到限制。然而,线框模型在计算时非常高效(因为只需要显示和处理顶点和边)。例如,线框模型可用于预览对象。在渲染复杂模型或动画序列时,或者要渲染所有对象,可能会非常耗时。如果有线框模型,就可以快速预览最终结果,而无需等待几分钟甚至几小时才能发现设计缺陷。
线框模型中的边缘不一定是线段。它们可以是曲线段,在这种情况下,边缘表将更复杂,因为除了两个端点之外,还需要对连接的曲线段进行描述(例如方程)。
2.边界表示法
边界表示法,简称 B-rep,可以看作是线框模型的扩展。B-rep 的优点在于实体以其表面为边界,并具有其内部和外部。一个实体的表面由一组面组成,面和面之间可能共享顶点和边。因此,B-rep 是对线框模型的扩展,在后者的基础上增加了面的信息。
B-rep中有两种类型的信息:拓扑信息和几何信息。拓扑信息提供了顶点、边和面之间的连接关系,类似于线框模型中描述的关系。除了连接关系,拓扑信息还包括边和面的方向。几何信息通常是指边和面的方程。
每个面的方向都很重要。通常,一个面由一组顶点围成。
使用右手定则,描述某些面的顶点排序时必须保证该面的法向量指向实体的外部。通常,逆时针表示的是顺序。如果该面由一个方程给出,则必须重写方程,以便面上每个点的法向量指向实体的外部。因此,通过检查面的法向量,可以立即判断当前位于B-rep 实体的内部还是外部。这种定向过程必须对所有面都进行。
以下显示了三个面及指外部的法向量。要描述顶面,顶点顺序应为6、7、2、1或7、2、1、6或2、1、6、7或1、6、7、2。要描述左侧面,顶点顺序应为1、2、3、4或2、3、4、1或3、4、1、2或4、1、2、3。
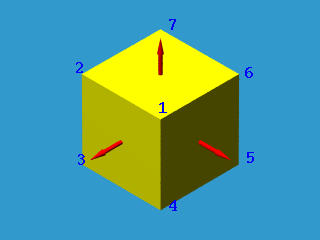
但是,并非所有的表面都可以以这种方式定向。如果实体的表面可以这样定向,那么它被称为可定向的; 否则,它是不可定向的。以下是众所周知的莫比乌斯环,它只有一个面,但是是不可定向的。

2.1 流形
一个实体的表面必须满足某些条件,这样得到的实体才是良好的。这就是所谓的流形条件。实体的表面不一定是流形,但我们仅讨论流形表面。
当且仅当对于表面上的每一点,都存在一个以为中心、半径足够小的开球(不封闭的球体),使得这个开球与表面的交集可以连续地变形为一个开圆盘,则这个表面是一个2-流形
一个以坐标原点为中心、半径为的开球方程为 。它包含了球 内的所有点。开圆盘的定义类似,由方程 定义。
所谓连续变形,是指可以在不切割(即必须保持邻接关系)和粘合(即需要一一对应关系)的情况下扭曲或弯曲形状。
如下图所示:
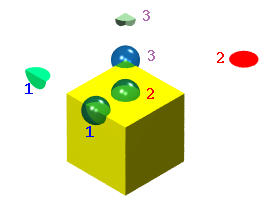
有一个立方体和三个开放的球。球体2的中心位于顶面。这个球与立方体表面的交集是一个开圆盘(用红色表示)。球1的中心位于一条边上。它与立方体表面的交集是一个弯曲的开圆盘,但可以展平使其成为一个开圆盘。球3的中心位于一个角落。它与立方体表面的交集是一个三路弯曲的开圆盘。
下图展示了一个表面不是流形的实体。开球与实体表面的交集是两个相交的开圆盘的并集。如果不 “粘合”,这个交集就无法变形为一个开圆盘。因此,这个实体表面不是流形的
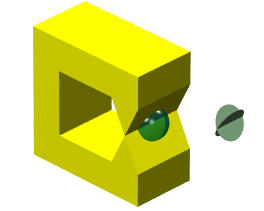
2.2 翼边数据结构
最古老的B-Rep数据结构可能是Baumgart的翼边数据结构。它与线框模型相同,因为翼边数据结构使用边来描述所有内容。
在下文,我们假设每个面上都没有孔洞,然后再对其扩展以处理孔洞。此外,我们假设边都是线段,面都是多边形。从拓扑学上讲,我们可以拉伸曲线边和面,使其变成直线和平面而不改变它们之间的连接关系。
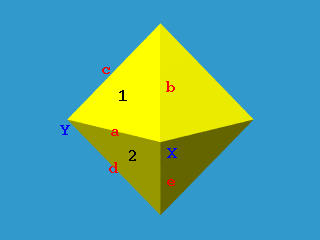
上图显示了一个多面体,其中顶点、边和面分别用大写字母、小写字母和数字表示。
其中边 有两个关联的顶点 和 ,以及两个关联的面 和 。面是由边围成的多边形。例如,面 有边 、 和 ,而面 有边 、 和 。
注意,从实体外部顺时针观察的排序。如果边的方向是从 到 ,那么面 和 就分别位于边 的右侧和左侧。
为了正确描述边的顺序,我们需要四个额外的信息。由于当遍历面 时边 会被遍历一次,当遍历面 时边 会被遍历第二次,它以不同方向被遍历两次。
例如,当遍历面 的边时,边 的前驱和后继是边 和边 ,而当遍历面 的边时,边 的前驱和后继是边 和边 。(即边的环绕顺序与面的法向符合右手定则)
尽管有四条边与顶点 相连,但在查找与边 关联的面时只用了与相连的其中三条边。因此,对于每条边,以下四个信息是重要的:
1.边的顶点
2.位于边左侧的面和右侧的面
3.当遍历其左侧面时,该边的前一条边和后一条边
4.当遍历其右侧面时,该边的前一条边和后一条边
边表:
边表中每行都包含了前面提到的信息:边的名称、起始顶点和终止顶点、左侧面和右侧面、在遍历左侧面时的前一条边和后一条边,以及在遍历右侧面时的前一条边和后一条边。
注意,这里使用的是顺时针的排序(从多面体外部看)。边的方向是从到。如果将方向改变为从到,那么下表中的数据必须相应地进行更改。

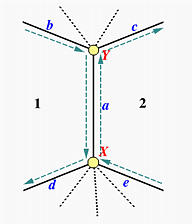
上面显示了边 的拓扑信息。边、、 和 四条边是边的翼,因此边是有翼的。
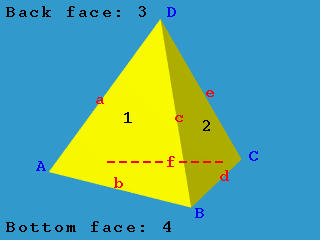
上图是一个四面体,有四个顶点和,六条边和,以及四个面(背)和(底)。其边表如下:
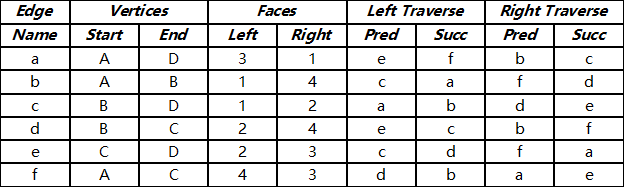
其他表格:
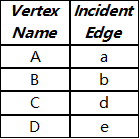
翼边数据结构需要另外两个表格,即 顶点表 和 面表。这两个表格非常简单。顶点表中对每个顶点对应一条与其关联的边。面表中每个面都对应一条边,这条边是这个面的边界边之一。
因此,我们有以下表格:
顶点表:
面表:
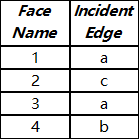
使用这种数据结构,可以清楚的知道哪些顶点、边、面与哪些面、边或顶点相邻。这种邻接关系共有九种。
例如,顶点是否与面5相邻? 面3和面5是否相邻? 翼边数据结构可以非常高效地进行查询。注意,一旦顶点、边和面的数量是已知的, 这三个表的大小就是固定的,不会改变。
带有孔洞的面
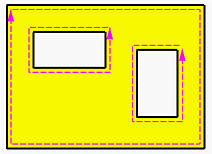
如果一个实体的某些表面有洞,上述的有翼边数据结构形式就无法表示。这些洞可能穿透整个实体(如下图左边的盒子)或者只是一个坑洞(如下图右边的盒子)。

解决这个问题有两种方法:
- 对于有内环的面,外边界顺时针排序,而内环(如果有)则逆时针排序。
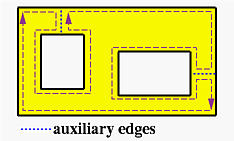
- 另一种简单的方法是在内环和外环之间添加一个辅助边,如下所示。这条辅助边将其左侧面和右侧面设为同一个面。这样,带有洞的面就变成了一个单独的环,可以用翼边数据结构来表示。在遍历循环时,由于辅助边的左侧面和右侧面相同,可以很容易识别出来。
2.3 欧拉-庞加莱(Euler-Poincaré)公式
欧拉-庞加莱(Euler-Poincaré)公式描述了流形几何的顶点数、边数和面数之间的关系。 它已经被推广到包括穿透实体的坑洞和孔洞形状。为了说明欧拉-庞加莱公式,我们先定义以下内容:
-
V: 顶点的数量
-
E: 边的数量
-
F: 面的数量
-
G: 穿透实体的孔洞数量,通常在拓扑学中称为属数(genus)。
-
S: 壳体的数量。壳是实体内部的空隙。一个壳体以一个二维流形表面为界,该表面可以有自己的属数(genus)。注意,实体本身也可以算作一个壳。因此,S的值至少为1。
-
L: 环的数量,包括外环和内环。
欧拉-庞加莱公式定义如下:
例子
- 一个立方体有八个顶点(V = 8),12条边(E = 12),六个面(F = 6),没有孔洞和一个壳(S = 1);但是L = F,因为每个面只有一个外循环。因此,我们有
-
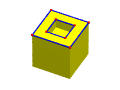
下面的实体有16个顶点,24条边,11个面,没有孔,1个壳和12个环(11个面+顶部面上的一个内环)。因此,

-
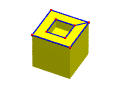
下面的实体有16个顶点、24条边、10个面、1个洞(即属值为 1)、1个壳和 12个环(10个面 + 上下两个面上的 2 个内环)。因此:

-
下面这个实体有一个贯穿孔和一个内部的立方体室,如右侧剖面图所示。它有24个顶点,(立方体)= 36条边,(立方体)- 2(顶部和底部开口)= 16个面,1个孔(即属为1),2个壳和18个环(16个面+顶部和底部面的2个内环)。因此:

-
下面的实体有两个穿透孔,并且没有内部孔洞,如右侧剖面图所示。它有24个顶点,36条边,14个面,2个孔(即属为2),1个壳和18个环(14个面 + 4)。因此,

B-rep记录的信息的一部分是拓扑关系(即邻接关系)。但是这种构造过程可能会生成无效的实体,检查这种拓扑无效性的一种方法是使用欧拉-庞加莱公式。如果其值不为零,那么可以肯定B-rep表示中一定有错误。然而,这只是一种单边检验, 欧拉-庞加莱公式的值为零并不意味着实体是有效的。

上图中有一个方框和一个额外的矩形。这个对象有10个顶点,15条边,7个面,1个壳体,没有孔。它的回路数等于面的数量。欧拉-庞加莱公式的值如下所示,
但这不是一个有效的实体!因此,如果欧拉-庞加莱公式的值非零,那么表示法表示的肯定不是一个有效实体。然而,欧拉-庞加莱公式的值为零并不保证表示的是一个有效实体。
如何正确计算属数(genus)?
要正确计算属数(假设为G) 并不容易。
假设一个球体上有三条隧道,如下图所示。左图显示的是球体外部。右图显示的是球体内部被切掉的一半。属值 G 是多少?
我们知道,属值计算的是穿透孔的数量。但在这个例子中,它有些模糊。将任意两个中心向隧道组合在一起,就会有三个贯穿孔,但是这是不正确的!
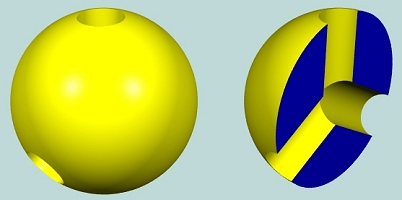
欧拉-庞加莱公式描述了顶点、边、面、环、壳和属的拓扑性质。
对模型施加的任何拓扑变换都不会改变这种关系。我们可以扭曲、拉伸和挤压模型,但不能切断某些部分,也不能粘合部分部分。我们可以压缩三条隧道周围的 “墙壁”,使模型内部变成一个薄壳。如下图所示:
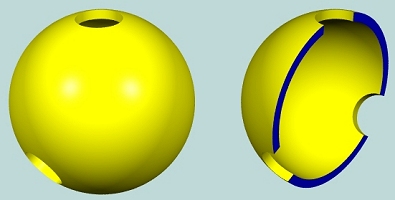
或者将顶部孔扩大到足够大(左下方)。然后,将顶部压平以使模型变平。如下图所示的右侧模型。有多少个穿透孔?两个!因此, 等于2。

有时,穿透的孔可能出现在不太可能的情况下。例如下面的模型,通过从球体的内部取出一个环面和一个管道得到。这个模型的属值是多少?它看起来并没有穿透的孔。所以,属值等于0吗?而实际上,

2.4 欧拉运算
一旦有了一个多面体模型,我们可能想通过添加或删除顶点、边和面来编辑它,从而创建一个新的多面体。这些操作被称为欧拉运算。事实证明,在使用欧拉运算编辑多面体的过程中,一些中间结果可能不是有效的实体。
回顾一下欧拉-庞加莱公式,对于所有的多面体,以下关系成立:
其中V,E,F,L,S和G分别是顶点数,边数,面数,环数,壳数和属数。
根据这个关系,我们使用一些欧拉算子来编辑多面体,以便满足欧拉-庞加莱公式。这些算子分为两组:构建(Make)和删除(Kill)。以M和K开头的运算符分别属于构建和删除操作。
欧拉算子记作和,分别表示在 Make 和 Kill 组中的操作,其中 , 和 是模型的元素(例如,顶点,边,面,环,壳和属)。例如,表示构建一条边和一个顶点,而 表示删除一条边和一个顶点。
Mantyla在1984年证明了欧拉算子构成了流形实体的一整套建模流程。准确的说,每个拓扑有效的多面体都可以通过一系列有限的欧拉运算从初始多面体构造出来。
欧拉运算中的构建操作
构建操作包括四个运算,用于将一些元素添加到现有模型中以创建新模型,还包含一个Make-Kill运算,用于同时添加和删除一些元素。以下是这些运算:
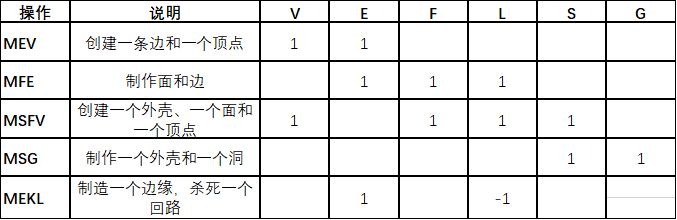
下表说明了使用欧拉运算构造四面体的方法。顶点、边和面分别用红色、蓝色和绿色表示;、壳用透明灰色表示。
第一步使用 MSFV 来创建一个只有一个面和一个顶点的壳。接下来的三步使用 MEV,每一步都会添加一条边和一个顶点。最后三步使用 MFE,每一步都会添加一个面和一条边。这样,通过七步欧拉运算,一个四面体就构建完成了。
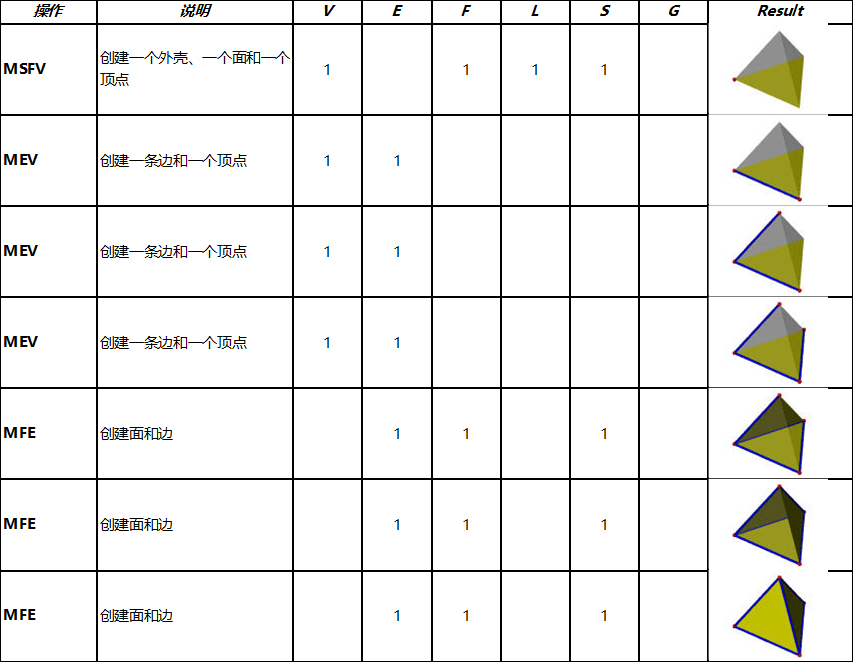
MSG只创建一个带孔洞的壳体。之后,可以添加顶点、边、面、环。壳体上必须要有环,因为新孔至少穿透一个面。
MEKL构建了一条边,同时删除了一个环。MEKL常用的情况是添加一条连接外环和内环的边。在这种情况下,边的数量增加了1,环的数量减少了1,因为那个环被“消除”了。
下面的左图显示了顶面的两个环,而右图显示了执行MEKL后添加的新边。因此,内部和外部通过新边连接在一起,成为一个单独的面。
欧拉运算的删除操作
删除的操作与构建的操作正好相反。事实上,将所有Make操作符中的 M 和 K 替换为 K 和 M,就得到了删除的操作符。因此,删除包括以下五个运算:
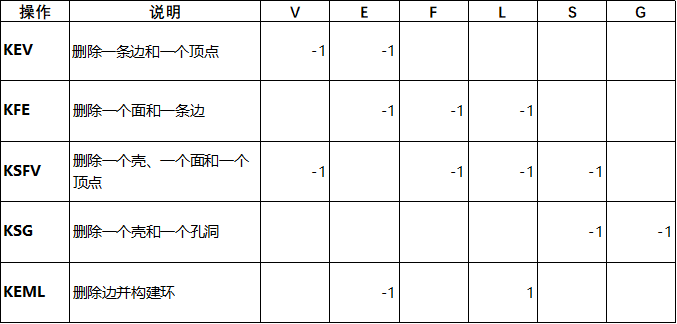
有了这些运算,我们就可以从一个四面体开始,将它化整为零。
3.构造实体几何
构造实体几何,简称CSG,是另一种表示实体的方式。CSG实体是由一些基本体以及布尔运算符(即并、交和差)构建而成的。因此,CSG实体可以用一种表达式的方式写出来(见下),CSG也被视为一种设计方法。
3.1 CSG基本图元
标准的CSG基本图元包括立方体(块)、三角形棱柱、球、圆柱、圆锥和圆环。这六个基本图元都是标准形状,用户需要首先将其实例化,实例化的基本图元可能需要进行缩放、平移和旋转等变换,才能变换到所需要的位置。
假设立方体由其“左下角” 和 “右上角” 定义。要生成一个中心点为,高度和宽度为3,长度为5的矩形,用户可以首先将立方体在 和 方向分别缩放1.5倍,在 方向缩放2.5倍,然后将结果平移到 。
假设在CSG过程中将立方体记为Block,则上述几何体可以按以下方式获得:
translate(scale(Block, ), )
3.2 布尔运算符
我们可以使用并集、交集和差集运算符将两个实例化的基本图元合并为一个。然而,简单的集合运算可能会产生问题,这一点将在正则化布尔运算符中讨论,因此需要进行修改。
给定两个集合, 和 ,
它们的并集包含来自 或 的所有点;
它们的交集为两个集合中共有的所有点;
它们的差集,写作 (相应地,),为包含在 中但不在 中的点(相应地,在 中但不在 中)。
假设 是垂直圆柱体, 是水平圆柱体。从左到右,四个实体分别是 和 的并集和交集,以及 和 。

因此,可以把实体视为对一组经过转换后的 CSG 基本图元应用布尔运算符的结果。
让我们看一个简单的例子。我们想设计一个如右图所示的带孔的支架形状。我们从两个立方体和一个圆柱体开始(最左边的图)。然后,两个方块被缩放,并且其中一个被旋转到垂直位置。圆柱也被缩放,使其半径与孔的半径相匹配。然后,这三个实例化被移动到它们对应的位置。随后计算两个立方体的并集,然后从中减去圆柱体,就得到了最终结果。




3.3 CSG表达式
上述支架的设计过程可以写成一个表达式:
diff(union(trans(Block1),trans(Block2)),trans(Cylinder))
其中union(A,B)和diff(A,B)分别表示A和B的并集和差集,trans()表示变换。或者,如果我们使用+、^和 - 表示集合的并集、交集和差集,上述表达式可以重写为以下形式:
(trans(Block1) + trans(Block2)) - trans(Cylinder)
该表达式可以转换为设计的表达式树,即CSG表达:
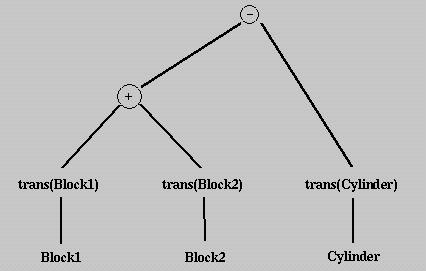
实际上,使用CSG方式构建的每个实体都有一个相应的CSG表达式,而这个表达式又有一个关联的CSG树。CSG树的表达式是最终设计的表示。相同的实体可能有不同的CSG表达式/树,CSG表示不是唯一的。
3.4 内部、外部和闭包
在讨论正则化布尔运算之前,我们先来聊一聊内部、外部和闭包的概念。
一个实体的内部由所有位于实体内部的点组成;
闭包由所有内部点和实体表面上的所有点组成;
而一个实体的外部是所有不属于闭包的点的集合。
一个球的方程为 。它的内部是满足 所有点的集合,而其闭包是。因此,闭包是内部和边界(其表面)的并集。显然,它的外部是。
实体是一个三维物体,因此它的内部和外部也是三维的。而它的边界是一个二维表面。
一般定义
以 为圆心、半径为 的开放球体包含了所有满足以下关系的点:
如果以 为圆心,半径为的开球完全包含在实体 中,则点 是实体 的内点。实体 的所有内点集合称为 的 内部,表示为 int(S)。根据这个定义,开球的内部就是开球本身。
如果以为圆心、半径的开球不与实体相交,则点是实体的外点。实体的所有外点集合称为实体的外部,表示为ext(S)。
不在实体 内部也不在其外部的点构成了该实体的边界,记为 b(S)。因此,实体的内部、外部和边界的并集就是整个空间。
实体 的闭包为 的内部和边界的并集,记为 closure(S)。
示例
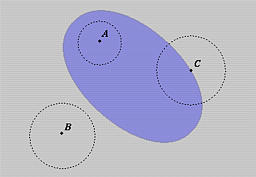
下图是平面上的一个例子。点 是阴影区域的内部点,点 是外部点。点 是边界点
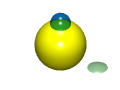
注意,表面(二维对象)永远不是实体(三维对象)。也就是说,表面没有任何内部点。取表面上的任意一点(见下图),以该点为中心、任意半径的开球总是与球面相交于一个开口圆盘(在右下角的淡绿色区域)。因此,我们有结论:曲面不包含任何内部点。
3.5 正则化布尔运算操作
我们期望两个实体的并集、交集和差集仍然是一个实体。但在许多情况下,事实并非总是如此。在下图中,两个立方体相互接触,它们的交集是一个矩形,如右图所示。二维平面中的矩形不是三维对象,因此也不是一个实体。

为了消除产生的这些低维结果,对这三种布尔运算进行了如下正则化处理(regularized):
- 按照通用的方式计算,产生低维度的结果。
- 计算结果的内部。这一步骤会删除所有低维度的部分。
- 计算在上述步骤中所得的结果的闭包。这会将边界添加回来。
假设+、^和 - 分别表示正则化集合的并集、交集和差集运算符。设和是两个实体。那么,、 ^ $ \mathbf{B}$和 定义如下:
= closure(int(和的并集))
^ = closure(int(和的交集))
- = closure(int(和的差集))
其中,closure() 和 int() 分别是在前文中讨论的闭包和内部运算符。
根据这一定义,本文开头所示的两个立方体的交集为空。这两个立方体的集合交集是一个矩形,是一个二维对象,没有内部。因此,在取内部(即int())后,得到一个空集,其闭包也是空集。因此,交集是空的。
3.6 CSG设计示例
假设需要设计三个互相垂直的管道,如下左图所示:

一个直观的方式是从一个较大的圆柱体中减去一个较小的圆柱体,得到一个如下右图所示的圆管。然后,取这个圆管的两个实例(再创建两个类似的圆管对象),每个实例都旋转一个适当的角度,计算这三个管道的并集,结果如下图所示。

但是,结果并不完全正确,如上图右侧所示,管道的内部连接处被阻塞了(因为管道求并集的过程中存在重叠的部分)。正确的解决方案是设计两个直径大小不同的三通管道,一个较大,另一个较小。然后,将较小的圆柱体从较大的圆柱体中减去,就得到了如下图所示的设计结果。








